A P. 5588. feladat (2024. szeptember)

P. 5588. Egy $\displaystyle R$ sugarú, vékony, $\displaystyle +Q$ töltéssel egyenletesen töltött szigetelőgyűrű vízszintes síkban helyezkedik el. A rögzített gyűrű átmérője mentén (pl. egy kifeszített horgászzsinóron) egy $\displaystyle +q$ töltésű, $\displaystyle m$ tömegű pontszerű test mozoghat súrlódásmentesen. A pontszerű testet egyensúlyi helyzetéből kicsit kitérítjük. Mekkora a bekövetkező kis rezgések periódusideje?

Közli: Vigh Máté, Biatorbágy

(6 pont)

A beküldési határidő 2024. október 15-én LEJÁRT.

I. megoldás. Határozzuk meg, hogy milyen elektromos mezőt hoz létre önmagában a töltött szigetelő gyűrű a középpontjának kicsiny környezetében. Ha azt kapjuk, hogy a gyűrű átmérője mentén az elektromos térerősség (jó közelítéssel) arányos a középponttól mért távolsággal, akkor már könnyen megadhatjuk a pontszerű, töltött test periodikus mozgásának rezgésidejét.

Válasszunk egy olyan koordináta-rendszert, amelynek origója a gyűrű középpontja, $\displaystyle z$ tengelye pedig a gyűrű síkjára merőleges szimmetriatengely. Ezen a tengelyen az origótól $\displaystyle z_0\ll R$ távol lévő pontban a hengerszimmetria miatt az elektromos térerősség nyilván $\displaystyle z$ irányú, nagysága pedig jó közelítéssel

$\displaystyle E_z(z_0)=k\frac{Q}{R^3}\,z_0.$

Ezt úgy láthatjuk be, hogy felosztjuk a gyűrűt sok kicsi, egyenként $\displaystyle \Delta Q$ töltésű darabkára (1. ábra), és ezek elektromos térerősségvektorait összegezzük.

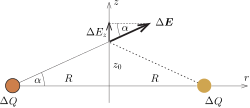
1. ábra

Az egyes darabok járuléka az elektromos mezőhöz $\displaystyle \vert{\Delta\boldsymbol E}\vert=k\frac{\Delta Q}{R^2+z_0^2}$ nagyságú, a térerősségvektor $\displaystyle z$ tengely irányú komponense pedig $\displaystyle \vert{\Delta\boldsymbol E}\vert$-nek $\displaystyle \sin\alpha=z_0/\sqrt{R^2+z_0^2}$-szerese:

$\displaystyle \Delta E_z(z_0)=k\frac{\Delta Q}{\left(R^2+z_0^2\right)^{3/2}}z_0\approx k\frac{\Delta Q}{R^3}z_0.$

(A nevezőben $\displaystyle z_0^2$-t elhanyagoltuk $\displaystyle R^2$ mellett, hiszen $\displaystyle z_0\ll R$. A képlet végén szereplő $\displaystyle z_0$ mennyiséget természetesen nem hanyagolhatjuk el, mert nincs mellette egy másik távolság, amihez képest nagyon kicsi lenne.)

A teljes gyűrű ($\displaystyle z$ irányú) elektromos terének (előjeles) nagysága, vagyis a $\displaystyle z$ komponense:

$\displaystyle E_z(z_0)=\sum k\frac{\Delta Q}{R^3}z_0=k\frac{z_0}{R^3}\sum\Delta Q=k\frac{Q}{R^3}z_0.$

Helyezzünk el – gondolatban – a gyűrű középpontjánál egy kicsiny hengert, amelynek alapköre $\displaystyle r_0$ sugarú, a magassága $\displaystyle 2z_0$, és a szimmetriatengelye a $\displaystyle z$ tengely (2. ábra). A hengerben nincsenek töltések, így – a Gauss-féle fluxustörvény szerint – a teljes felületén áthaladó $\displaystyle \Psi$ elektromos fluxus nulla.

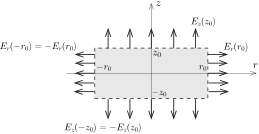
2. ábra

A henger két körlapján összesen

$\displaystyle \Psi_1=2E_z(z_0)\cdot r_0^2\pi$

fluxus távozik a hengerből. (Ez a megállapítás csak közelítőleg igaz, hiszen a körlapok mentén a térerősség $\displaystyle z$ komponensét ugyanakkorának veszi, mint amennyi az a szimmetriatengelyen, holott $\displaystyle E_z$ $\displaystyle z_0$-n kívül nyilván a tengelytől mért $\displaystyle r$ távolságtól is függhet. Ezt a függést azonban $\displaystyle r\le r_0\ll R$ miatt elhanyagolhatjuk, mert a fluxushoz csak $\displaystyle z_0$ vagy $\displaystyle r_0$ szorzatával (esetleg magasabb hatványaikkal) arányos, tehát nagyon kicsiny járulékot ad.)

A henger palástján keresztül kilépő fluxus

$\displaystyle \Psi_2=E_r(r_0)\cdot 2\pi r_0\cdot 2z_0.$

(Ez az összefüggés is tartalmaz közelítést, mert elhanyagolja, hogy $\displaystyle E_r(r)$ nemcsak $\displaystyle r_0$-tól, hanem $\displaystyle z$-től is függhet. Ez a függés azonban $\displaystyle z_0\ll R$ miatt ugyancsak ,,másodrendűen kicsi'' korrekciót eredményez a fluxus kiszámításánál.)

A teljes elektromos fluxus $\displaystyle \Psi_1+\Psi_2=0$, vagyis

$\displaystyle 2k\frac{Q}{R^3}z_0\cdot r_0^2\pi+E_r(r_0)\cdot 2\pi r_0\cdot 2z_0=0.$

Innen leolvasható, hogy

$\displaystyle E_r(r_0)=-k\frac{Q}{2R^3}\,r_0.$

Ennek megfelelően a horgászzsinóron csúszkáló, $\displaystyle q$ töltésű pontszerű testre ható erő az origótól $\displaystyle r$ távolságban

$\displaystyle F(r)=-k\frac{qQ}{2R^3}\,r\equiv -D\cdot r.$

(A negatív előjel arra utal, hogy az erő az egyensúlyi helyzet felé mutató vektor, tehát $\displaystyle r=0$ stabil egyensúlyi helyzet.)

A fenti erőtörvény éppen olyan, mint egy $\displaystyle D$ direkciós erejű rugónál, a kialakuló mozgás periódusideje tehát

$\displaystyle T=2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{2mR^3}{kqQ}}.$

Megjegyzés. Az alkalmazott közelítések alapja az, hogy az elrendezés a $\displaystyle z$ tengelyre nézve forgásszimmetrikus, a gyűrű síkjára nézve pedig tükörszimmetrikus. Tekintsük pl. a térerősséget egy a szimmetriasíktól $\displaystyle z$, a forgástengelytől $\displaystyle r$ távolságra levő pontban! A gyűrű síkjára való tükrözéskor a radiális komponens nem változhat, tehát $\displaystyle z$-nek csak páros hatványitól függhet, míg a síkra merőleges komponensnek előjelet kell váltania, tehát $\displaystyle z$ páratlan függvénye. Ennek megfelelően egy a $\displaystyle z$ tengellyel párhuzamos egyenes mentén a radiális komponensnek szélsőértéke (maximuma) van a gyűrű síkjában, és ettől távolodva az értéke csak $\displaystyle z$ négyzetével vagy annál lassabban változhat. Mivel bármely sík, ami a forgástengelyt tartalmazza, maga tükörsík, gondolatmenetünket egy ilyen síkra megismételve azt találjuk, hogy a térerősség $\displaystyle z$ irányú komponense a $\displaystyle z$ tengelytől mért $\displaystyle r$ távolság páros függvénye lehet csak, így a tengely közelében csak lassan, legfeljebb $\displaystyle r^2$-tel arányosan változhat.

Összefoglalva: Az elektromos térerősség hengerkoordináta-rendszerbeli komponensei az origó közelében így írhatók fel:

$\displaystyle E_r(r,z)=a_1r+a_2rz^2+\cdots\approx a_1r,$

$\displaystyle E_z(r,z)=b_1z+b_2zr^2+\cdots\approx b_1z.$

Látható, hogy abban a közelítésben, hogy $\displaystyle r$ és $\displaystyle z$ 1-nél magasabb kitevőjű hatványai elhanyagoljuk, $\displaystyle E_z$ nem függ $\displaystyle r$-től és arányos $\displaystyle z$-vel, $\displaystyle E_r$ pedig $\displaystyle z$-től független és $\displaystyle r$-rel arányos.

II. megoldás. Az $\displaystyle E_r(r)$ térerősséget, kicsit több munka árán, direkt módon is kiszámíthatjuk. Osszuk fel a gyűrűt $\displaystyle R\Delta\varphi$ hosszúságú kicsiny ívekre, és számoljuk ki ezen darabok járulékát a gyűrű síkjában fekvő, a forgástengelytől $\displaystyle r$ távolságra levő $\displaystyle P$ pontban! (A jelöléseket a 3. ábra mutatja.)

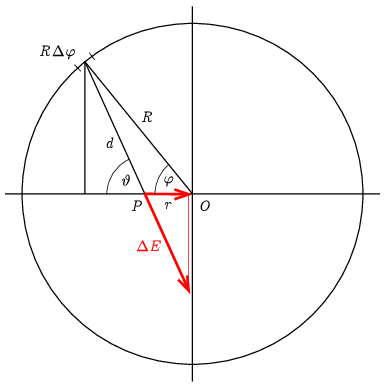
3. ábra

A bejelölt $\displaystyle R\Delta\varphi$ hosszúságú szakasz $\displaystyle \Delta Q=\Delta\varphi(Q/2\pi)$ töltése által létrehozott térerősség $\displaystyle OP$ irányú komponensének a nagysága a $\displaystyle P$ pontban

$\displaystyle \Delta E_r=\Delta E\cos\vartheta=-k\frac{\Delta Q}{d^2}\cos\vartheta.$

(A járulék erre merőleges komponensével nem kell számolnunk, mert az az összegzés során a szimmetria miatt kiesik.) A koszinusztétel segítségével

$\displaystyle d=\sqrt{R^2+r^2-2Rr\cos\varphi}\qquad\textrm{és}\qquad\cos\vartheta=\frac{R\cos\varphi-r}{d}=\frac{R\cos\varphi-r}{\sqrt{R^2+r^2-2Rr\cos\varphi}},$

így

$\displaystyle \Delta E_r=-k\Delta Q\frac{R\cos\varphi-r}{\left(\sqrt{R^2+r^2-2Rr\cos\varphi}\right)^3},$

ami $\displaystyle R$ kiemelése után

$\displaystyle \Delta E_r=-\frac{k\Delta Q}{R^2}\frac{\cos\varphi-(r/R)}{\left(\sqrt{1+(r/R)^2-2(r/R)\cos\varphi}\right)^3}.$

alakú. Feltételezésünk szerint $\displaystyle r\ll R$, így alkalmazhatjuk az $\displaystyle \vert x\vert\ll 1$ értékekre érvényes $\displaystyle (1+x)^{-n/m}\approx (1-nx/m)$ közelítést, és az $\displaystyle (r/R)^2$-tel arányos tagokat az egy nagyságrendű tagok mellett elhanyagolhatjuk. Így a

$\displaystyle \Delta E_r=-\frac{k\Delta Q}{R^2}\left(\cos\varphi+\frac{r}{R}\left(3\cos^2\varphi-1\right)\right)=-\frac{k\Delta Q}{R^2}\left(\cos\varphi+\frac{r}{R}\left(\frac{1}{2}+\frac{3}{2}\cos(2\varphi)\right)\right)$

kifejezésre jutunk. Ezt és $\displaystyle \Delta Q$ értékét felhasználva

$\displaystyle E_r(r)=-\frac{kQ}{R^2}\frac{1}{2\pi}\sum\left(\cos\varphi+\frac{r}{R}\left(\frac{1}{2}+\frac{3}{2}\cos(2\varphi)\right)\right)\Delta\varphi.$

Mivel a teljes $\displaystyle 0\le\varphi\le2\pi$ tartományra nézve mind $\displaystyle \sum\cos\varphi\Delta\varphi$, mind pedig $\displaystyle \sum\cos(2\varphi)\Delta\varphi$ nulla, viszont $\displaystyle \sum\Delta\varphi=2\pi$,

$\displaystyle E_r(r)=-\frac{kQ}{2R^3}r.$

A horgászzsinóron csúszkáló pontszerű testre ható erő az origótól $\displaystyle r$ távolságban

$\displaystyle F(r)=-k\frac{qQ}{2R^3}\,r\equiv -D\cdot r.$

A kialakuló mozgás harmonikus rezgőmozgás, amelynek rezgésideje

$\displaystyle T=2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{2mR^3}{kqQ}}.$

Statisztika:

19 dolgozat érkezett.
6 pontot kapott:	Beke Márton Csaba, Bencz Benedek, Gyenes Károly, Kiss 131 Adorján Timon, Simon János Dániel, Tóth Kolos Barnabás.
5 pontot kapott:	Csiszár András.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2024. szeptemberi fizika feladatai