A P. 5591. feladat (2024. október)

P. 5591. Három különböző fizikai ingát készítünk.

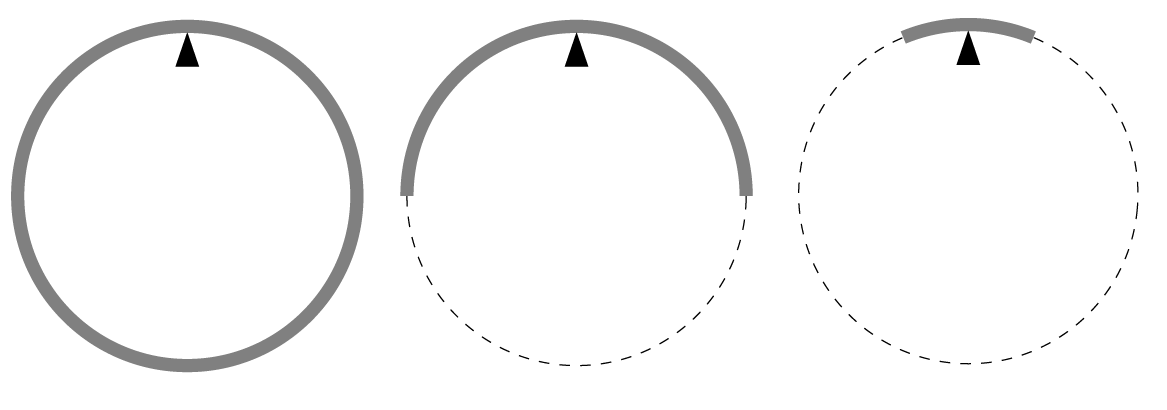
$\displaystyle a)$ Egy $\displaystyle R$ sugarú körré hajlított, homogén tömegeloszlású, vékony rudat az egyik pontjánál egy ékkel belülről alátámasztunk. A kör alakú rúd szabadon elfordulhat az ék körül a saját síkjában.

$\displaystyle b)$ Egy ugyanilyen sugárban meghajlított rúdból félkört vágunk ki, és azt a hosszának felénél támasztjuk alá.

$\displaystyle c)$ Az előző esethez hasonlóan járunk el, de csak egy viszonylag rövid, nyolcadkör alakú körívet helyezünk a közepénél az ékre.

Mindhárom ingát kicsit kitérítjük, és megmérjük a lengéseik periódusidejét. Vajon melyik lengésidő lesz a leghosszabb, és melyik a legrövidebb?

Közli: Cserti József, Budapest

(5 pont)

A beküldési határidő 2024. november 15-én LEJÁRT.

Megoldás. Jelöljük a kör középpontját $\displaystyle O$-val, a belőle kivágott ív tömegét $\displaystyle m$-mel, az $\displaystyle S$ tömegközéppont és a $\displaystyle P$ alátámasztási pont távolságát pedig $\displaystyle s$-sel. ($\displaystyle s$ függ a körív ,,nyílásszögétől''.) A fizikai inga lengésidő-képlete szerint

$\displaystyle T=2\pi\sqrt{\frac{\Theta_P}{mgs}},$

ahol $\displaystyle \Theta_P$ a körívnek a $\displaystyle P$ pontra vonatkoztatott tehetetlenségi nyomatéka.

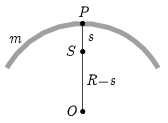
Számítsuk ki $\displaystyle \Theta_P$-t a Steiner-tétel felhasználásával! Nyilván $\displaystyle \Theta_O=mR^2$, hiszen az ív minden pontja $\displaystyle R$ távol van a kör középpontjától. Alkalmazzuk a Steiner-tételt a $\displaystyle P$ pontra és az $\displaystyle O$ pontra:

$\displaystyle \Theta_P=\Theta_S+ms^2,$

$\displaystyle \Theta_O=\Theta_S+m(R-s)^2.$

A két egyenlet különbségéből $\displaystyle \Theta_S$ kiesik:

$\displaystyle \Theta_P-mR^2=ms^2-m(R-s)^2,$

vagyis

$\displaystyle \Theta_P=2mRs,$

a lengésidő tehát

$\displaystyle T=2\pi\sqrt{\frac{\Theta_P}{mgs}}=2\pi\sqrt{\frac{2R}{g}}.$

Meglepő módon a lengésidő nem függ $\displaystyle s$-től, vagyis nem függ a körív nyílásszögétől. A feltett kérdésekre tehát az a válasz, hogy mindhárom alakzat lengésideje (kis kitérések esetén) ugyanakkora.

Statisztika:

28 dolgozat érkezett.
5 pontot kapott:	Agócs Zoltán, Beke Márton Csaba, Erdélyi Dominik, Gyenes Károly, Simon János Dániel, Tóth Hanga Katalin.
4 pontot kapott:	Csiszár András, Horváth 001 Botond , Ujpál Bálint.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2024. októberi fizika feladatai