A P. 5598. feladat (2024. november)

P. 5598. Tom McPoint, a híres akrobata a hírek szerint 2024 telén Hódmezővásárhelyen is bemutatja legendás mutatványát, amelyben egy toronyház tetejére rögzítés nélkül ráfektetett, az utca fölé kinyúló deszkapalló végére kisétálva integet a nézőközönségnek. A produkciót megelőző napon az akrobata segédei vízzel fellocsolják a kiválasztott ház vízszintes tetejét, hogy tükörsima jégpáncél alakuljon ki rajta, majd a mutatvány kezdőpillanatában a jégre fektetett, \(\displaystyle 6\) méter hosszú pallót olyan hosszan tolják ki a tető szélén túl, hogy még éppen ne billenjen le, ha Tom a tetőn maradt végére rááll (ábra).

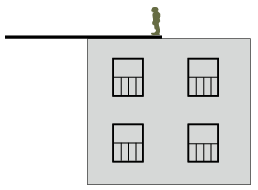
a) Legfeljebb milyen hosszú lehet a mutatvány kezdetén a deszkapalló utca fölé kinyúló része, ha Tom \(\displaystyle 60~\mathrm{kg}\), a palló pedig \(\displaystyle 40~\mathrm{kg}\) tömegű?

b) Milyen messze lesz Tom a mutatvány végén a háztető szélétől, ha állandó nagyságú sebességgel \(\displaystyle 20~\mathrm{s}\) alatt végigsétál a deszkán?

A palló és a jég között fellépő súrlódás elhanyagolható, a mutatvány során Tom talpa nem csúszik meg a deszka felületén.

Tornyai Sándor fizikaverseny, Hódmezővásárhely

(4 pont)

A beküldési határidő 2024. december 16-án LEJÁRT.

Megoldás. a) Az \(\displaystyle M=60\,\mathrm{kg}\) tömegű ember és az \(\displaystyle m=40\,\mathrm{kg}\) tömegű, \(\displaystyle \ell=6\,\mathrm{m}\) hosszúságú palló közös tömegközéppontjának a ház felett kell lennie, határesetben épp a ház pereménél. A tömegközéppont távolsága a palló közepétől:

\(\displaystyle s=\frac{M\frac{\ell}{2}}{M+m}=1{,}8\,\mathrm{m},\)

így a pallónak legfeljebb

\(\displaystyle x=\frac{d}{2}+s=4{,}8\,\mathrm{m}\)

hosszúságú darabja lóghat ki az utca fölé.

b) A pallóból és az emberből álló rendszerre a jég elhanyagolható súrlódása miatt nem hat vízszintes irányú erő, így miközben Tom lassan kisétál a palló végére, a palló és az ember közös tömegközéppontja egy helyben marad. A legvégén Tom a palló másik végén áll, így ekkor a tömegközéppont ismét \(\displaystyle s\) távolságra lesz a palló középpontjától (csak most a másik irányba). A tömegközéppont változatlanul a ház pereménél van, így a pallóból most

\(\displaystyle y=\frac{d}{2}-s=1{,}2\,\mathrm{m}\)

lóg ki az utca fölé, Tom is ilyen messze lesz a ház peremétől.

Statisztika:

56 dolgozat érkezett.
4 pontot kapott:	Agócs Zoltán, Bélteki Teó, Bense Tamás, Bús László Teodor, Csipkó Hanga Zoé , Csiszár András, Domján Noémi Dóra, Erős Fanni, Fekete Lúcia, Földi Albert, Gyenes Károly, Hornok Máté, Horvath Benedek, Kirst Alexander, Kis Boglárka 08, Klement Tamás, Kovács Tamás, Ligeti Barnabás, Magyar Zsófia, Masa Barnabás, Misik Balázs, Monok Péter, Nagy Gellért Ákos, Papp Emese Petra, Sütő Áron, Szabó Donát, Szabó Márton, Szécsi Bence, Tóth-Tűri Bence, Ujpál Bálint, Varga 511 Vivien, Vértesi Janka, Vincze Anna, Zólomy Csanád Zsolt.
3 pontot kapott:	Gőbel Hanka, Konkoly Zoltán, Molnár Lili, Zámbó Luca.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2024. novemberi fizika feladatai