 |
A P. 5599. feladat (2024. november) |
P. 5599. Egy forgási paraboloid alakú, függőleges szimmetriatengelyű, vékony fémserleget az O csúcsánál vízszintes tartólaphoz erősítettünk. A P pont és a síklap távolsága h0. A serleg belsejében elhelyezett vékony csőbe, annak Q végpontjánál egy pontszerű testet ejtettünk, amely a serleg P pontjánál hagyja el a csövet. A Q és a P pont magasságkülönbsége H.
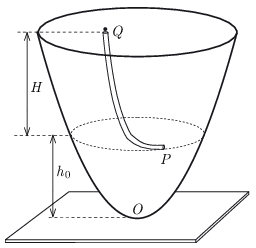
A kis test a serleg érintősíkjában fekvő, vízszintes egyenes irányában repül ki a csőből. Milyen határok között fog változni a kis testnek a lemeztől mért h távolsága a további mozgás során? (A súrlódás mindenhol elhanyagolható.)
Közli: Gnädig Péter, Vácduka
(5 pont)
A beküldési határidő 2024. december 16-án LEJÁRT.
Megoldás. A kis test v0=√2gH sebességgel hagyja el a csövet a P pontnál. Legyen a P pont távolsága a szimmetriatengelytől r0, a lemeztől mért távolsága pedig h0. Mivel a felület forgási paraboloid, fennáll, hogy
| (1) | h0=kr20, |
ahol k egy állandó.
Abban a helyzetben, ahol a test h magassága maximális vagy minimális, a függőleges irányú sebességkomponens nulla, és így a szimmetriatengely felé mutató ,,radiális'' sebesség is nulla. A test sebessége tehát ebben a pontban ,,érintő irányú''. Ha a kérdéses pontban a tengelytől mért távolság r, akkor a test magassága
| (2) | h=kr2. |
A perdületmegmaradás törvénye szerint
| (3) | mr0v0=mrv, |
az energiamegmaradás törvénye szerint pedig fennáll:
| (4) | 12mv20+mgh0=12mv2+mgh. |
A (4) egyenlet
12(v20−v2)=g(h−h0)
alakját (1) (2) és (3)-ból kapható v2=v20h0h összefüggés felhasználásával így is felírhatjuk:
v202(h−h0)=(h−h0)gh.
Mivel a triviális h=h0 esettől különböző megoldást keresünk, egyszerűsíthetünk (h−h0)-lal:
v202=gh,
vagyis
h=v202g=H.
A kis test távolsága tehát H>h0 esetén h0≤h≤H értékek között változik, H<h0 esetben pedig H≤h≤h0.
Megjegyzés. Ha H=h0, akkor a test körpályán, egyenletes körmozgással kering. Ezt a mozgásegyenletből is megkaphatjuk. A serleg által kifejtett N nyomóerő függőleges komponense
N2=mg,
hiszen a test függőleges irányban nem gyorsul.
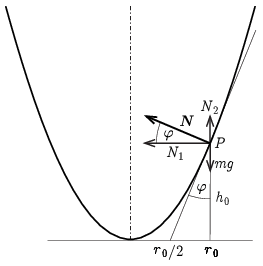
Az ábrán látható hasonló derékszögű háromszögek oldalaránya megegyezik:
N1N2=2h0r0,
vagyis
N1=2h0r0mg.
Ez az erő akkor tud létrehozni r0 sugarú körpályán egyenletes, v0 sebességű körmozgást, ha
mv20r0=mg2h0r0,
vagyis
v20=2gh0=2gH,
azaz H=h0.
Statisztika:
15 dolgozat érkezett. 5 pontot kapott: Csiszár András, Kovács Tamás, Masa Barnabás, Molnár Lili, Molnár Zétény, Tóthpál-Demeter Márk, Ujvári Sarolta. 4 pontot kapott: Agócs Zoltán, Kis Boglárka 08. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. novemberi fizika feladatai
|
|

