A P. 5600. feladat (2024. november)

P. 5600. A vízszintes, súrlódásmentes talajon álló létra két egyforma szára kezdetben $\displaystyle \varphi_0$ szöget zár be a talajjal, és a köztük lévő lánc akadályozza meg a szétcsúszásukat. A létra tetején egy $\displaystyle M$ tömegű ember ül. A lánc elszakad, a létra szétnyílik. Mekkora sebességgel és gyorsulással ér talajt az ember? Hogyan aránylik ez a két mennyiség ahhoz, amikor az ember ugyanekkora magasságból szabadon esik le? Vizsgáljuk az $\displaystyle M\to 0$, illetve az $\displaystyle M\to\infty$ határeseteket. Tekintsük a létra szárait egy-egy $\displaystyle m$ tömegű, $\displaystyle \ell$ hosszúságú homogén rúdnak, az embert pedig pontszerűnek. A létra két szárát felül egy súrlódásmentes csukló tartja össze.

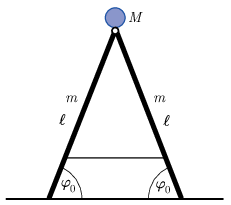
Közli: Cserti József, Budapest

(5 pont)

A beküldési határidő 2024. december 16-án LEJÁRT.

Megoldás: Jelölje $\displaystyle F_1$ azt az erőt, amivel a talaj felfelé, és $\displaystyle F_2$ azt, amivel az ember lefelé nyomja az egyes létraszárakat. Ezek az erők függőlegesek. A létra szárai között vízszintes erő is hat, de azzal nem kell foglalkoznunk, mert a földetéréskor nincs a létraszárakra ható forgatónyomatéka, így még közvetve sem befolyásolja az ember gyorsulást ebben a pillanatban. A geometriából világos, hogy ha az ember, azaz a létra csúcsának a sebessége és a gyorsulása rendre $\displaystyle v$ és $\displaystyle a$, akkor a létraszárak tömegközéppontjainak a függőleges sebessége és gyorsulása $\displaystyle v/2$ és $\displaystyle a/2$, és a földetérés pillanatában az egyes ágak szögsebessége és szöggyorsulása $\displaystyle \omega=v/\ell$ ill. $\displaystyle \beta=a/\ell$.

A kérdéses sebességet legegyszerűbben az energia-egyenletből kaphatjuk meg:

$\displaystyle \frac{1}{2}Mv^2+2\cdot\frac{1}{2}m\left(\frac{v}{2}\right)^2+2\cdot\frac{1}{2}\cdot\frac{1}{12}m\ell^2\left(\frac{v}{\ell}\right)^2=(M+m)\ell g\sin\varphi_0.$

Ebben az egyenletben a bal oldalon az első tag az ember, a második a létraszárak tömegközépponti mozgásának, a harmadik pedig a tömegközéppont körüli forgásának a kinetikus energiája, és felhasználtuk, hogy egy $\displaystyle m$ tömegű, $\displaystyle \ell$ hosszúságú homogén rúd tömegközéppontjára vonatkoztatott tehetetlenségi nyomatéka $\displaystyle (1/12)m\ell^2$. Ebből a sebesség

$\displaystyle v=v_0\sqrt{\frac{3\left(m+M\right)}{2m+3M}},$

ahol

$\displaystyle v_0=\sqrt{2g\ell\sin\varphi_0}$

a földetérés sebessége lenne a $\displaystyle h=\ell\sin{\varphi_0}$ magasságból történő szabadesés esetén.

A keresett gyorsulás meghatározásához írjuk fel az erő és a forgatónyomaték egyenleteket (ez utóbbit a létra ágak tömegközéppontjára) a földetérés pillanatában!

A három egyenletből a gyorsulásra

$\displaystyle a=g\frac{3\left(m+M\right)}{2m+3M}$

adódik.

Az $\displaystyle M\to\infty$ határértékben $\displaystyle M$ mellett $\displaystyle m$ elhanyagolható, ilyenkor $\displaystyle v=v_0$ és $\displaystyle a=g$, mintha a létra ott sem lenne. Ha $\displaystyle M\to0$, akkor $\displaystyle v=\sqrt{3/2}v_0$ és $\displaystyle a=(3/2)g$. (Bár ilyenkor $\displaystyle v>v_0$ és $\displaystyle a>g$, ebben nincs ellentmondás: tulajdonképpen a létra ágak tömegközéppontja ,,esik", ennek a sebessége és a gyorsulása a földetéréskor $\displaystyle \sqrt{3/8}v_0<v_0$ és $\displaystyle (3/4)g<g$. Ugyanakkor, ha az ember nem kapaszkodik a létrába, akkor az esés közben valahol elválik, és szabadeséssel folytatja útját. A nagyobb sebességű és gyorsulású becsapódás csak kapaszkodás esetén jöhet létre, ha áll a létrán, akkor nem.)

Megjegyzés. A megoldásban a létraszárak mozgását felbontottuk a tömegközéppont transzlációjára és egy forgásra, de leírhattuk volna az egészet egyben, mint a földön lévő végpont (pillanatnyi forgástengely) körüli forgást. Ha így járunk el, a nehézségi erő és az $\displaystyle F_2$ forgatónyomatékával kell számolnunk, $\displaystyle F_1$ nem jelenik meg, és egyenesen az

$\displaystyle \frac{1}{3}m\ell^2\left(\frac{a}{\ell}\right)=mg \frac{\ell}{2}+F_2\ell$

egyenletet kapjuk. (Akkor egyszerű a pillanatnyi forgástengelyhez rögzített koordináta rendszert használnunk, ha az inerciarendszer, vagy ha gyorsul ugyan, de az ebből adódó tehetetlenségi erőnek nincs forgatónyomatéka a pillanatnyi forgástengelyre. Esetünkben a becsapódás pillanatában ez utóbbi feltétel teljesül.)

Statisztika:

24 dolgozat érkezett.
5 pontot kapott:	Beke Márton Csaba, Erdélyi Dominik, Molnár Zétény, Simon János Dániel, Tóth Hanga Katalin, Vértesi Janka, Zólomy Csanád Zsolt.
4 pontot kapott:	Klement Tamás, Papp Emese Petra, Vincze Anna.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. novemberi fizika feladatai