A P. 5604. feladat (2024. november)

P. 5604. Egy laposelem üresjárási feszültsége $\displaystyle U_0=4{,}5~\mathrm{V}$, belső ellenállása $\displaystyle R_\mathrm{b}=1{,}5~\Omega$. Van két egyforma izzólámpánk, amelyek $\displaystyle I(U)$ karakterisztikája az ábrán látható.

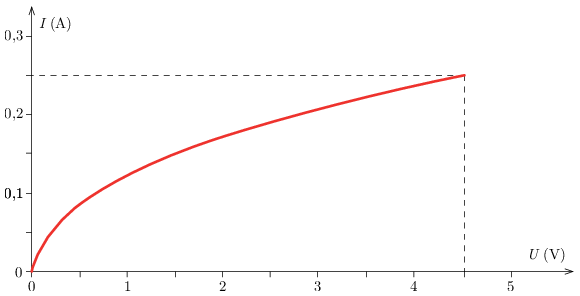
a) Hogyan függ a telep kapocsfeszültsége a terhelő áramtól? Ábrázoljuk a telep $\displaystyle I(U)$ karakterisztikáját!

b) Egy izzót rákapcsolunk a telepre. Határozzuk meg az izzóra eső feszültséget és az izzón átfolyó áramot (az ún. munkapontot) az $\displaystyle I(U)$ grafikon segítségével!

c) A két izzót

    i) párhuzamosan,

    ii) sorba

kapcsoljuk, és így kötjük rá a telepre. Készítsük el a párhuzamosan, illetve a sorba kapcsolt izzók (együttes) $\displaystyle I(U)$ karakterisztikáját, majd határozzuk meg mindkét esetben az új munkapontot. Ezután határozzuk meg mindkét esetben az egy izzóra eső feszültséget és az izzón átfolyó áramot!

Közli: Vankó Péter, Budapest

(5 pont)

A beküldési határidő 2024. december 16-án LEJÁRT.

Megoldás. a) A belső ellenálláson $\displaystyle U_\mathrm{b}=R_\mathrm{b}I$ feszültség esik, így a kapocsfeszültség $\displaystyle U=U_0-R_\mathrm{b}I$. Ez alapján a telep árama a kapocsfeszültség függvényében

$\displaystyle I=\frac{U_0-U}{R_\mathrm{b}},$

amely grafikusan az 1. ábrán látható. (Figyelem! A grafikon skálája más.)

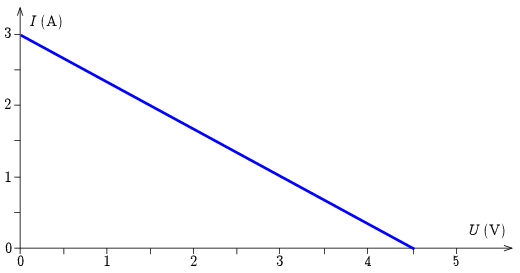
1. ábra

Megjegyzés. Az $\displaystyle I_\mathrm{r}=\tfrac{U_0}{R_\mathrm{b}}$ áramot rövidzárási áramnak nevezzük, ilyenkor a kapocsfeszültség nulla. Az $\displaystyle U_0$ feszültséget szokás üresjárási feszültségnek is nevezni, ilyenkor a telepen át folyó áram nulla.

b) Rajzoljuk a telep és az izzó karakterisztikáját közös grafikonba!

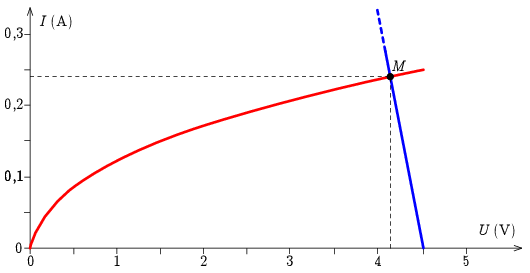
2. ábra

A munkapont ($\displaystyle M$) a két görbe metszéspontja. A grafikonról leolvasva:

$\displaystyle U_1\approx 4{,}14\,\mathrm{V}\quad\textrm{és}\quad I_1\approx 0{,}240\,\mathrm{A}.$

c) Ha a két izzót párhuzamosan kapcsoljuk, akkor feszültségük megegyezik, áramaik összeadódnak. Az eredő kapcsolás karakterisztikáját az eredeti izzókarakterisztika kétszeres függőleges nyújtásával kapjuk meg (a grafikonon sárga görbe). A soros kapcsolás esetében a két izzó árama egyezik meg, és feszültségeik adódnak össze, így ekkor a karakterisztikát vízszintesen kell kétszeresére megnyújtani (a grafikonon zöld görbe). Ezután a munkapontokat az előzőhöz hasonlóan szerkeszthetjük meg.

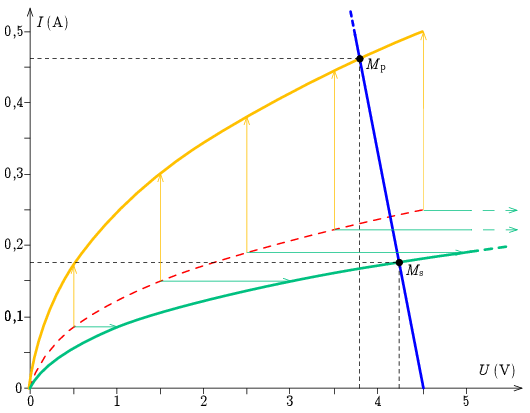
3. ábra

A grafikonról leolvasva párhuzamos esetben a munkapont ($\displaystyle M_\mathrm{p}$) $\displaystyle U_\mathrm{p}\approx 3{,}80\,\mathrm{V}$ és $\displaystyle I_\mathrm{p}\approx 0{,}462\,\mathrm{A}$, soros esetben pedig ($\displaystyle M_\mathrm{s}$) $\displaystyle U_\mathrm{s}\approx 4{,}24\,\mathrm{V}$ és $\displaystyle I_\mathrm{s}\approx 0{,}176\,\mathrm{A}$. Ebből már könnyen meghatározhatjuk mindkét esetben egy-egy izzó feszültségét és áramát:

Statisztika:

12 dolgozat érkezett.
5 pontot kapott:	Csipkó Hanga Zoé , Sütő Áron, Ujpál Bálint.
4 pontot kapott:	Blaskovics Ádám, Fekete Lúcia, Masa Barnabás, Simon János Dániel.
3 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. novemberi fizika feladatai