A P. 5607. feladat (2024. december)

P. 5607. Egy rögzített lejtő tetejéről vízszintesen elhajított kicsiny test éppen a lejtő aljánál csapódik be (ábra). A becsapódáskor a sebessége a lejtő síkjával $\displaystyle {\beta=19^\circ}$-os szöget zár be. Mekkora a lejtő hajlásszöge?

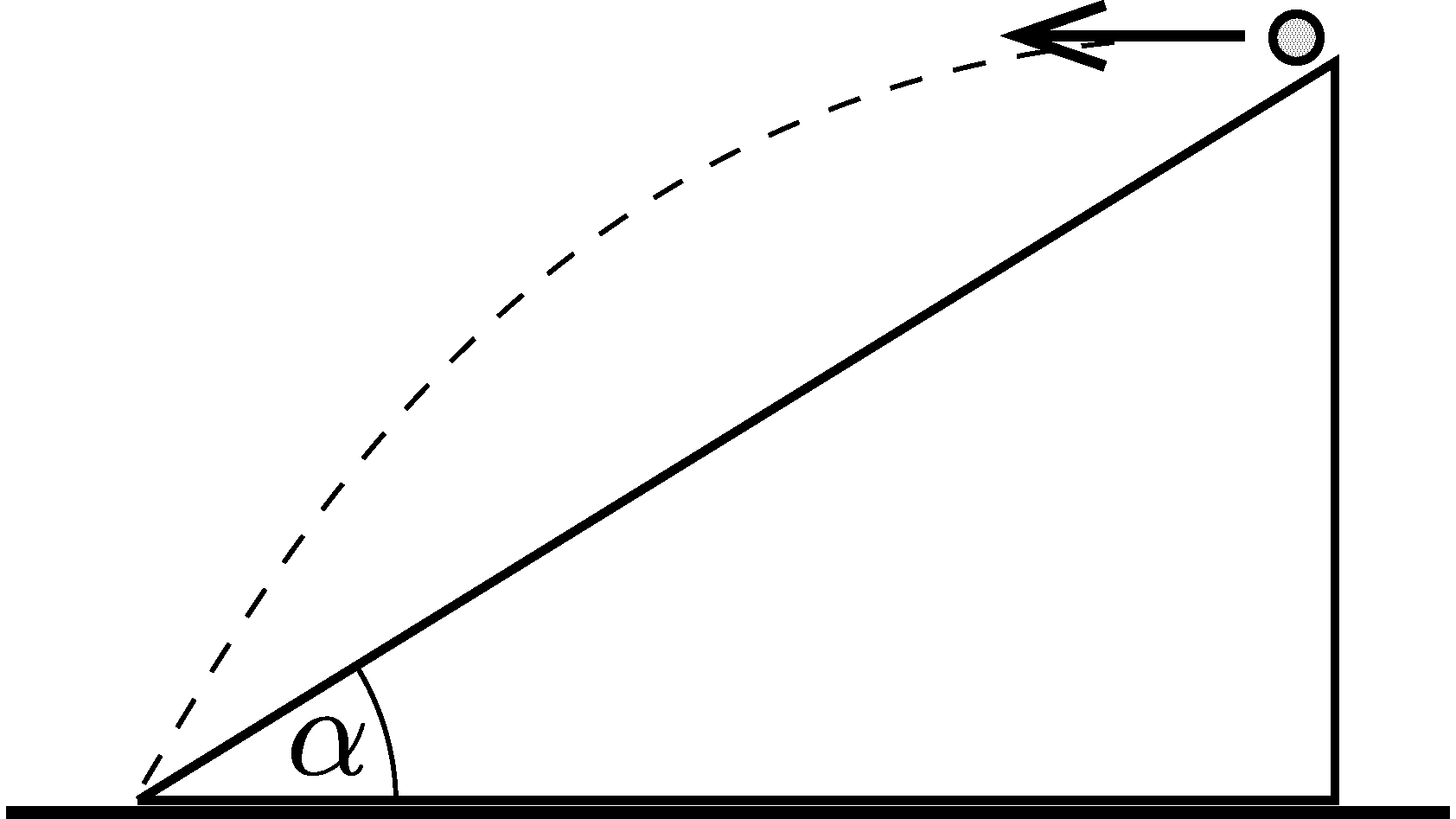
Közli: Zsigri Ferenc, (Budapest)

(3 pont)

A beküldési határidő 2025. január 15-én LEJÁRT.

Megoldás. Jelöljük a lejtő alapjának hosszát $\displaystyle d$-vel, a lejtő magassága ekkor $\displaystyle h=d\tg\alpha$. A függőleges mozgás $\displaystyle h$ magasságból induló szabadesés, az ideje tehát

$\displaystyle t=\sqrt{\frac{2d\tg\alpha}{g}}.$

A becsapódáskor a test függőleges irányú sebessége

$\displaystyle v_y=gt=\sqrt{2gd\tg\alpha}.$

A test vízszintes irányban egyenletesen mozog, a sebessége

$\displaystyle v_x=\frac{d}{t}=\sqrt{\frac{gd}{2\tg\alpha}}.$

A becsapódáskor a test sebessége a vízszintessel $\displaystyle \alpha+\beta$ szöget zár be, fennáll tehát

$\displaystyle \tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\cdot\tg\beta}=\frac{v_y}{v_x}=2\tg\alpha.$

A fentebbi egyenlet így is felírható:

$\displaystyle 2\tg\beta\cdot\tg^2\alpha-\tg\alpha+\tg\beta=0,$

ami az $\displaystyle X\equiv\tg\alpha$ változóra nézve másodfokú egyenlet.

Tudjuk még, hogy $\displaystyle \beta=19^\circ,$ vagyis $\displaystyle \tg\beta=0{,}344.$ Az egyenlet két gyöke:

$\displaystyle X_1=0{,}56\qquad\textrm{és}\qquad X_2=0{,}89,$

amelyek a lejtő $\displaystyle \alpha_1\approx 29^\circ$-os és $\displaystyle \alpha_2\approx 42^\circ$-os hajlásszögének felelnek meg. A feladat feltételeinek ezen szögek bármelyike eleget tesz.

Statisztika:

41 dolgozat érkezett.
3 pontot kapott:	Bálint Áron, Beinschroth Máté, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Éliás Kristóf , Fekete Lúcia, Fercsák Flórián, Illés Dóra, Kis Boglárka 08, Klement Tamás, Konkoly Zoltán, Magyar Zsófia, Misik Balázs, Molnár Lili, Papp Emese Petra, Sütő Áron, Szabó Donát, Szécsi Bence, Tóth Hanga Katalin, Tóth-Tűri Bence, Ujvári Sarolta, Vértesi Janka, Vincze Anna.
2 pontot kapott:	Csipkó Hanga Zoé , Sipos Márton, Varga 511 Vivien, Zámbó Luca.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2024. decemberi fizika feladatai