 |
A P. 5609. feladat (2024. december) |
P. 5609. Egy \(\displaystyle 330~\mathrm{ml}\)-es üdítőitalos dobozt közelítsünk homogén tömegeloszlású hengerfelülettel, melynek magassága \(\displaystyle H=14{,}6~\mathrm{cm}\), belső átmérője \(\displaystyle d=5{,}4~\mathrm{cm}\). A doboz tömege \(\displaystyle M=14~\mathrm{g}\). Mennyi vizet töltsünk a dobozba, hogy a lehető legalacsonyabban legyen a rendszer tömegközéppontja? Milyen magasan van ekkor a tömegközéppont?
Közli: Szentivánszki Soma, Budapest
(4 pont)
A beküldési határidő 2025. január 15-én LEJÁRT.
I. megoldás. Amíg a tömegközéppont a vízszint felett van, addig a dobozba vizet öntve a tömegközéppont süllyedni fog, hiszen ekkor a dobozból és a már benne lévő vízből álló rendszerhez a tömegközéppontja alatt adunk hozzá egy újabb tömeget, amely a tömegközéppontot így lejjebb viszi. Ugyanígy, ha a tömegközéppont a vízszint alatt van, akkor további víz hozzáadása a rendszer tömegközéppontját emeli. A tömegközéppont tehát akkor lesz a legmélyebben, ha éppen a víz felszínén lesz.
A doboz és a víz tömegközéppontja is a magasságuk felénél helyezkedik el. Legyen a keresett vízszint magassága \(\displaystyle h\), a víz tömege \(\displaystyle m=\varrho Ah\) (ahol \(\displaystyle A=\tfrac{d^2\pi}{4}\)). Ekkor a rendszer tömegközéppontjának magassága a tömegközéppont definíciója szerint:
\(\displaystyle h_\mathrm{tkp}=\frac{M\frac{H}{2}+m\frac{h}{2}}{M+m}=\frac{MH+mh}{2(M+m)}=\frac{MH+\varrho Ah^2}{2(M+\varrho Ah)}.\)
Felhasználva, hogy az előbbi gondolatmenet alapján a keresett helyzetben \(\displaystyle h_\mathrm{tkp}=h\), adódik a
\(\displaystyle h_\mathrm{tkp}=\frac{MH+\varrho Ah^2}{2(M+\varrho Ah)}=h,\)
egyenlet, amely rendezve \(\displaystyle h\)-ra másodfokú:
\(\displaystyle \varrho Ah^2+2Mh-MH=0,\)
és pozitív megoldása a keresett vízmagasság:
\(\displaystyle h=\frac{-M+\sqrt{M^2+MH\varrho A}}{\varrho A}=2{,}44\,\mathrm{cm}.\)
Gondolatmenetünk alapján a tömegközéppont magassága is ugyanekkora.
II. megoldás. Az előző megoldás jelöléseivel a tömegközéppont magassága \(\displaystyle h\) függvényében:
\(\displaystyle h_\mathrm{tkp}=\frac{MH+\varrho Ah^2}{2(M+\varrho Ah)}.\)
Ennek szélsőértékét deriválással, a számtani és mértani közepek közötti egyenlőtlenséggel vagy grafikusan határozhatjuk meg.
II/1. megoldás: deriválással.
\(\displaystyle \frac{\mathrm{d}h_\mathrm{tkp}}{\mathrm{d}h}=\frac{4\varrho Ah(M+\varrho Ah)-2\varrho A(MH+\varrho Ah^2)}{4(M+\varrho Ah)^2}=0,\)
amiből rendezéssel az I. megoldásban szereplővel azonos másodfokú egyenletet kapjuk:
\(\displaystyle \varrho Ah^2+2Mh-MH=0,\)
melynek pozitív megoldása a keresett vízmagasság:
\(\displaystyle h=\frac{-M+\sqrt{M^2+MH\varrho A}}{\varrho A}=2{,}44\,\mathrm{cm}.\)
Ezt behelyettesítve a tömegközéppont magasságának kifejezésébe:
$$\begin{align*} h_\mathrm{tkp}&=\frac{MH+\varrho Ah^2}{2(M+\varrho Ah)}=\\ &=\frac{MH+\varrho A\frac{M^2-2M\sqrt{M^2+MH\varrho A}+M^2+MH\varrho A}{(\varrho A)^2}}{2\left(M-M+\sqrt{M^2+MH\varrho A}\right)}=\\ &=\frac{MH\varrho A+M^2-2M\sqrt{M^2+MH\varrho A}+M^2+MH\varrho A}{2\varrho A\sqrt{M^2+MH\varrho A}}=\\ &=\frac{-M\sqrt{M^2+MH\varrho A}+M^2+MH\varrho A}{\varrho A\sqrt{M^2+MH\varrho A}}=\\ &=\frac{-M+\sqrt{M^2+MH\varrho A}}{\varrho A}=h=2{,}44\,\mathrm{cm}. \end{align*}$$Megjegyzés. A behelyettesítést numerikus adatokkal is el lehet végezni, akkor egyszerűbb.
II/2. megoldás: egyenlőtlenséggel. Alakítsuk át \(\displaystyle h_\mathrm{tkp}\) kifejezését és használjuk fel a számtani és mértani közepek egyenlőtlenségét. Ebből adódik a tömegközéppont magasságának minimális értéke:
$$\begin{align*} h_\mathrm{tkp}&=\frac{MH+\varrho Ah^2}{2(M+\varrho Ah)}=\\ &=\frac{1}{\varrho A}\frac{M^2+MH\varrho A+\left(\varrho Ah\right)^2-M^2}{2(\varrho Ah+M)}=\\ &=\frac{1}{\varrho A}\frac{(\varrho Ah+M)(\varrho Ah-M)+M^2+MH\varrho A}{2(\varrho Ah+M)}=\\ &=\frac{1}{\varrho A}\frac{\varrho Ah-M+\frac{M^2+MH\varrho A}{\varrho Ah+M}}{2}=\\ &=\frac{1}{\varrho A}\frac{-2M+\varrho Ah+M+\frac{M^2+MH\varrho A}{\varrho Ah+M}}{2}=\\ &=\frac{1}{\varrho A}\left(-M+\frac{(\varrho Ah+M)+\frac{M^2+MH\varrho A}{\varrho Ah+M}}{2}\right)\geq\\ &\geq\frac{-M+\sqrt{M^2+MH\varrho A}}{\varrho A}=2{,}44\,\mathrm{cm}. \end{align*}$$A minimális értéket akkor veszi fel \(\displaystyle h_\mathrm{tkp}\), ha
\(\displaystyle \varrho Ah+M=\frac{M^2+MH\varrho A}{\varrho Ah+M},\)
amiből \(\displaystyle h\) értéke ekkor:
\(\displaystyle h=\frac{-M+\sqrt{M^2+MH\varrho A}}{\varrho A}=2{,}44\,\mathrm{cm}.\)
II/3. megoldás: grafikonnal. Helyettesítsük be a paramétereket a \(\displaystyle h_\mathrm{tkp}(h)\) függvénybe (a hosszakat cm-ben, a tömeget g-ban, a sűrűséget \(\displaystyle \mathrm{g/cm^3}\)-ben). Ekkor \(\displaystyle h_\mathrm{tkp}\) kifejezése cm-ben:
\(\displaystyle h_\mathrm{tkp}=\frac{MH+\varrho Ah^2}{2(M+\varrho Ah)}=\frac{204{,}4+22{,}90h^2}{28+45{,}80h},\)
és ábrázoljuk a függvényt:
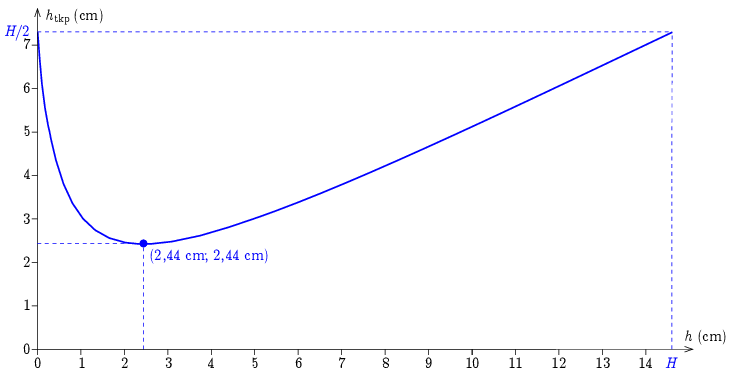
A grafikonról leolvasható a minimum helye és értéke is.
Statisztika:
54 dolgozat érkezett. 4 pontot kapott: Agócs Zoltán, Bélteki Teó, Bencze Mátyás, Blaskovics Ádám, Csipkó Hanga Zoé , Csiszár András, Erdélyi Dominik, Fekete Lúcia, Gyenes Károly, Hasulyó Dorián, Hornok Máté, Horvath Benedek, Hübner Júlia, Kis Boglárka 08, Klement Tamás, Kovács Tamás, Masa Barnabás, Molnár Lili, Monok Péter, Papp Emese Petra, Sárecz Bence, Simon János Dániel, Sütő Áron, Tóthpál-Demeter Márk, Ujpál Bálint, Varga 511 Vivien, Vincze Anna. 3 pontot kapott: Balázs Barnabás, Bálint Áron, Beke Márton Csaba, Bense Tamás, Bús László Teodor, Éliás Kristóf , Fercsák Flórián, Illés Dóra, Magyar Zsófia, Pituk Péter, Zámbó Luca, Zólomy Csanád Zsolt. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 3 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. decemberi fizika feladatai