A P. 5611. feladat (2024. december)

P. 5611. Az ábrán látható ,,kettős jojó'' két egyforma, homogén tömegeloszlású korongból és a rájuk tekert fonalakból áll.

A két testet a fonalak függőleges helyzetéből kezdősebesség nélkül indítjuk el.

a) Melyik korong tengelyének lesz nagyobb a sebessége egy bizonyos idő elteltével, és hányszorosa ez a sebesség a másik korongénak?

b) Melyik korong szögsebessége lesz nagyobb egy bizonyos idő elteltével, és hányszorosa ez a szögsebesség a másik korongénak?

(A kérdéses pillanatban a fonalak még nem tekeredtek le a korongokról.)

Közli: Gnädig Péter, Vácduka

(5 pont)

A beküldési határidő 2025. január 15-én LEJÁRT.

Megoldás. Legyen a korongok tömege $\displaystyle m$, sugara $\displaystyle r$, a felső korong tömegközéppontjának gyorsulása $\displaystyle a_1$, szöggyorsulása $\displaystyle \beta_1$, az alsó korongé $\displaystyle a_2$ és $\displaystyle \beta_2$. A felső fonalat feszítő erőt jelölje $\displaystyle K_1$, az alsó fonálban ható erőt pedig $\displaystyle K_2$ (lásd az ábrát).

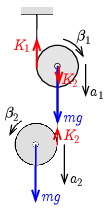
A következő mozgásegyenleteket írhatjuk fel:

A fonalak hosszának állandósága miatt fennállnak még az

és az

kényszerfeltételek.

Az (1)-(6) lineáris egyenletrendszer megoldásából kapjuk:

$\displaystyle a_1=\cfrac{8}{11}g\qquad \text{és}\qquad a_2=\cfrac{10}{11}g,$

továbbá

$\displaystyle \beta_1=\frac{8}{11}\,\frac{g}{r}\qquad \text{és}\qquad \beta_2=\frac{2}{11}\,\frac{g}{r}.$

a) A korongok tömegközéppontja egyenletesen gyorsul, a sebességük tehát egy adott idő múlva a gyorsulásukkal arányos. Eszerint az alsó korong sebessége bármely időpontban nagyobb, mint a felső korongé:

$\displaystyle \frac{v_2}{v_1}=\frac{a_2}{a_1}=\frac{5}{4}.$

b) A korongok szöggyorsulása állandó, a szögsebességek tehát egy adott pillanatban a szöggyorsulással arányosak:

$\displaystyle \frac{\omega_1}{\omega_2}=\frac{\beta_1}{\beta_2}=4,$

tehát a felső korong szögsebessége lesz nagyobb az indulás utáni időpillanatokban.

Statisztika:

25 dolgozat érkezett.
5 pontot kapott:	Beke Márton Csaba, Bélteki Teó, Csiszár András, Erdélyi Dominik, Erős Fanni, Gyenes Károly, Kiss 131 Adorján Timon, Masa Barnabás, Molnár Lili, Nagy Gellért Ákos, Papp Emese Petra, Pázmándi József Áron, Sütő Áron, Szécsi Bence, Tóth Hanga Katalin, Tóthpál-Demeter Márk, Ujpál Bálint, Zólomy Csanád Zsolt.
4 pontot kapott:	Kovács Tamás.
3 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. decemberi fizika feladatai