A P. 5612. feladat (2024. december)

P. 5612. $\displaystyle 25~^\circ\mathrm{C}$-os nitrogéngázzal $\displaystyle 1000~\mathrm{J}$ hőt közlünk, miközben állandó hőmérsékleten kitágul. Ezután a gázt adiabatikusan tágítjuk, amelynek hatására $\displaystyle 0~^\circ\mathrm{C}$ hőmérsékletre hűl. Ugyanebbe a végállapotba juthattunk volna, ha a gázt először adiabatikusan, majd izotermikusan tágítjuk. Mennyi hőt kellene ebben az esetben közölni a gázzal az izoterm folyamat során?

Közli: Széchenyi Gábor, Budapest

(4 pont)

A beküldési határidő 2025. január 15-én LEJÁRT.

Megoldás. Vázoljuk fel a folyamatokat egy $\displaystyle p-V$ diagramon! Ezen az $\displaystyle AB$ és a $\displaystyle DC$ szakasz a $\displaystyle T_1=298\,\mathrm{K}$-hez illetve a $\displaystyle T_2=273\,\mathrm{K}$-hez tartozó izoterma egy-egy darabja, az $\displaystyle AD$ és a $\displaystyle BD$ szakaszok adiabaták, $\displaystyle Q_1=1000\,\mathrm{J}$ és a keresett $\displaystyle Q_2$ a megfelelő szakaszokon felvett hőmennyiségek, ha a folyamatok a bejelölt irányban mennek végbe.

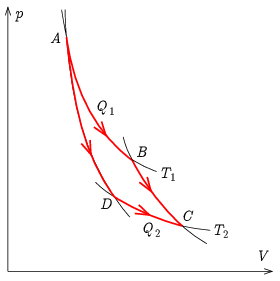
Ha a rendszert az $\displaystyle A\rightarrow B\rightarrow C\rightarrow D\rightarrow A$ irányban körbe vinnénk, a rendszer egy teljes Carnot-ciklust járna be, amelyben $\displaystyle Q_1$ a felső hőtartályból felvett, $\displaystyle Q_2$ pedig az alsó hőtartálynak leadott hő lenne. Egy ilyen hőerőgépnek a hatásfoka az ismert módon

$\displaystyle \frac{Q_1-Q_2}{Q_1}=\frac{T_1-T_2}{T_1},$

amiből

$\displaystyle Q_2=Q_1\frac{T_2}{T_1}=916\,\mathrm{J}.$

Statisztika:

22 dolgozat érkezett.
4 pontot kapott:	Bélteki Teó, Bús László Teodor, Csiszár András, Fekete Lúcia, Masa Barnabás, Simon János Dániel, Tóth-Tűri Bence, Vértesi Janka.
3 pontot kapott:	Bálint Áron, Hornok Máté, Ujvári Sarolta.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2024. decemberi fizika feladatai