A P. 5615. feladat (2024. december)

P. 5615. Egy $\displaystyle U_0=4~\mathrm{V}$ feszültségű ideális telep, egy $\displaystyle R=0{,}5~\Omega$ ellenállású fogyasztó, egy kapcsoló és két dürisztor (D) felhasználásával az a) ábrán látható kapcsolást állítjuk össze. A dürisztor egy olyan áramköri elem, amely egy $\displaystyle L=1~\mathrm{H}$ induktivitású ideális tekercs és egy nemlineáris $\displaystyle r$ ellenállás soros kapcsolásából áll. Az ellenállás $\displaystyle U_r(I_\mathrm{D})$ karakterisztikáját a b) ábra mutatja.

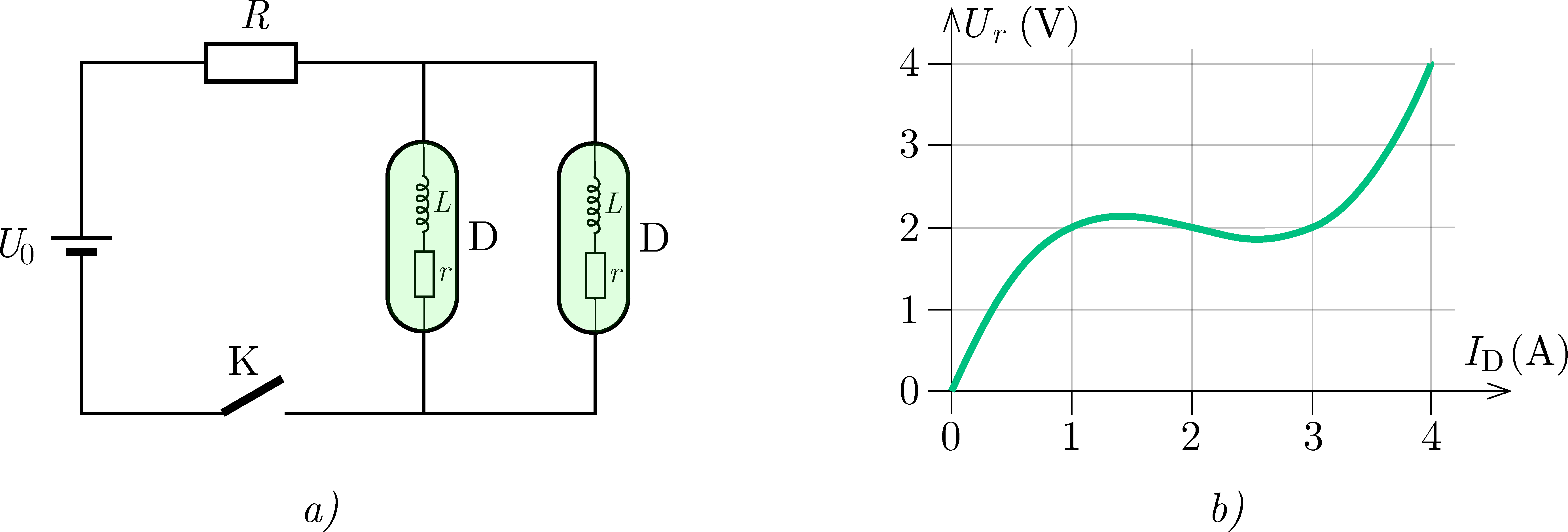
a) Mekkorák lehetnek stacionárius (azaz időben állandó) esetben a mellékágakban folyó áramok?

Segítség: Lásd a P. 5604. feladatot és annak megoldását a munkafüzetben.

b) A $\displaystyle t=0$ pillanatban bekapcsoljuk a kapcsolót. Vázoljuk fel a dürisztorokon átfolyó áramokat az idő függvényében. Mekkorák lesznek ezek az áramok hosszabb idő után?

Segítség: Tegyük fel, hogy eközben a szimmetria miatt a két dürisztoron azonos áram folyik.

c) Az egyensúlyi állapotban egy kis zavar keletkezik: az egyik dürisztor árama egy nagyon kicsit lecsökken, a másiké pedig ugyanennyivel megnő. Vázoljuk fel a két dürisztor áramát ezután az idő függvényében. Mekkorák lesznek az egyes dürisztorok áramai hosszabb idő után? Mit állíthatunk az a) kérdésben megadott stacionárius megoldások stabilitásáról?

Segítség: Felhasználhatjuk, hogy ha a kis zavar az első egyensúlyi állapothoz képest szimmetrikus, akkor a két dürisztor áramának összege állandó marad.

Dürer Verseny feladata nyomán

(6 pont)

A beküldési határidő 2025. január 15-én LEJÁRT.

Megoldás. a) A két párhuzamosan kapcsolt dürisztor teljes $\displaystyle U(I)$ karakterisztikáját azokon a feszültségeken, amelyekhez csak egy lehetséges áramérték tartozik, a megadott karakterisztika vízszintesen kétszeresére nyújtásával kaphatjuk meg, a P. 5604. feladat megoldásához hasonlóan. Ahol több (két vagy három) lehetséges áramérték tartozik egy feszültséghez, ott ezek tetszőleges kombinációja (akár hat különböző érték) lehet az eredő áram, így ezen a tartományon a vízszintesen kétszeresére megnyújtott görbén kívül újabb ágak jelennek meg. Ezek jellegzetes pontjait grafikus összeadással szerkeszthetjük meg.

Megjegyzés. A szerkesztés négy különböző esetben az 1. ábrán látható (a jobb láthatóság miatt a rajz nagyított és függőleges irányban meg van nyújtva).

A legalsó (fekete) pontnál a feszültséghez csak egy áramérték tartozik, így a párhuzamosan kapcsolt dürisztorok karakterisztikáján csak egy pont keletkezik, amelynek áramértéke az eredeti karakterisztikán lévő áramérték kétszerese. Ezt a pontot megkapjuk a karakterisztika nyújtásával is.

A következő esetben a feszültség éppen a karakterisztika lokális minimumához tartozó érték, ezt két különböző áramértéknél veszi fel (kék pöttyök). A párhuzamos kapcsolás árama lehet mindkettő duplája (ezeket adja meg a teljes grafikon vízszintes irányú nyújtása), de lehet a két áramérték összege is (1+2). Ugyanígy járhatnánk el a karakterisztika lokális maximumánál is.

A harmadik eset a karakterisztika középpontjához tartozó feszültségérték: itt az eredeti karakterisztikán három lehetséges áramérték van (lila pöttyök). Ezekből bármely kettő összege lehet a párhuzamos kapcsolás árama. A nyújtással is megkapható 1+1, 2+2 és 3+3 pontokon kívül megkapjuk az 1+2, 1+3 és 2+3 pontokat is – de ezek közül az 1+3 egybeesik a 2+2 ponttal, így itt öt lehetséges érték van.

A negyedik (narancs) esetben nincs ilyen egybeesés, ott mind a hat áramérték különböző. De erre a szerkesztésre már a grafikon megrajzolásához nincs is szükség: ha a második eset szerkesztését megismételjük a lokális maximumnál is, akkor a harmadik eset pontjaival együtt már megkapjuk a ,,kis ág'' minden fontos pontját (elágazás, keresztezés, szélsőértékek), amely alapján már a teljes karakterisztika felvázolható.

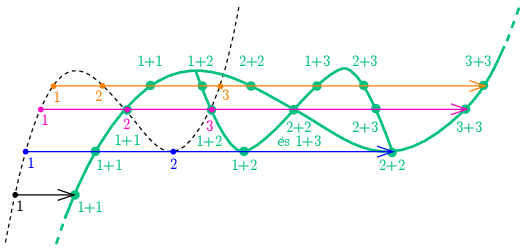
1. ábra

A végeredmény a 2. ábrán látható, amelybe már berajzoltuk a telep és az $\displaystyle R$ ellenállás együttes $\displaystyle U(I)$ karakterisztikáját is. A két görbe – esetünkben egyetlen – metszéspontja adja meg a párhuzamos kapcsolás stacionárius munkapontját: a dürisztorokon $\displaystyle U_\mathrm{D}=2\,\mathrm{V}$ feszültség esik, és összesen $\displaystyle I_{\Sigma\mathrm{D}}=4\,\mathrm{A}$ áram folyik. (Stacionárius állapotban a tekercsek feszültsége nulla, a dürisztor teljes feszültsége megegyezik a karakterisztikáról leolvashatóval.)

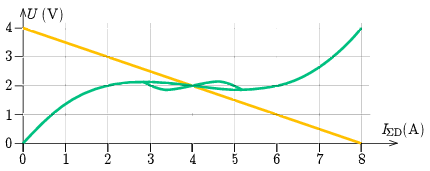
2. ábra

Visszatérve egyetlen dürisztor karakterisztikájára (3. ábra) látható, hogy ez kétféleképpen valósulhat meg: vagy mindkét dürisztoron $\displaystyle I_\mathrm{D1}=I_\mathrm{D2}=2\,\mathrm{A}$ áram folyik, vagy pedig az egyiken $\displaystyle I_\mathrm{D1}=1\,\mathrm{A}$ és a másikon $\displaystyle I_\mathrm{D2}=3\,\mathrm{A}$.

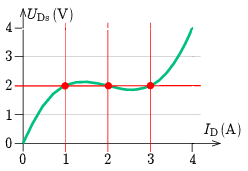
3. ábra

b) Bekapcsoláskor mindenhol nulla áram folyik, a külső és a dürisztorokban lévő belső ellenálláson se esik feszültség, a teljes $\displaystyle U_0=4\,\mathrm{V}$ telepfeszültség a dürisztorokban lévő tekercsekre esik. Mivel $\displaystyle U_L=L\dot I_L=L\dot I_\mathrm{D}$, a tekercsek (és így a dürisztor) árama, valamint a külső ellenállás $\displaystyle 2I_\mathrm{D}$ árama is nőni fog. Ezzel változik a külső és belső ellenállásokon a feszültség is: a külső ellenálláson lineárisan ($\displaystyle U_R=2RI_\mathrm{D}$), a belső ellenállásokon a megadott nemlineáris karakterisztika szerint. A tekercsekre így kisebb feszültség jut, az áram növekedése lassul, de folytatódik mindaddig, amíg a tekercsre eső feszültség pozitív, azaz a külső és belső ellenállásokon eső feszültség nem éri el a telep feszültségét. Szimmetrikus esetben ez az $\displaystyle I_\mathrm{D}=2\,\mathrm{A}$ és $\displaystyle U_\mathrm{D}=2\,\mathrm{V}$ állapotban következik be, amikor $\displaystyle U_R=2RI_\mathrm{D}=2\,\mathrm{V}$ és $\displaystyle U_\mathrm{D}+U_R=U_0=4\,\mathrm{V}$. Tehát hosszabb idő után a dürisztorok árama $\displaystyle I_\mathrm{D1}=I_\mathrm{D2}=2\,\mathrm{A}$. Az áramok időfüggése a 4. ábrán látható. (A pontos görbealak és az időskála csak numerikus számítással kapható meg, de a görbe jellege a fenti gondolatmenet alapján felvázolható.)

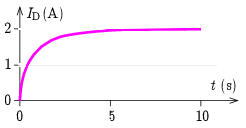
4. ábra

c) Jelöljük a b) részben kialakult egyensúlyi áramot és feszültséget $\displaystyle I_\mathrm{D0}$-lal és $\displaystyle U_\mathrm{D0}$-lal. A hirtelen kis zavar hatására $\displaystyle I_\mathrm{D1}<I_\mathrm{D0}<I_\mathrm{D2}$, de eközben $\displaystyle I_\mathrm{D1}+I_\mathrm{D2}=2I_\mathrm{D0}$, és így $\displaystyle U_R$ és $\displaystyle U_\mathrm{D}=U_0-U_R$ állandó marad. Az 1. dürisztorban lévő ellenálláson a kicsit lecsökkent áram miatt $\displaystyle U_{r1}>U_\mathrm{D0}$ feszültség esik, az ebben lévő tekercs feszültsége így negatív lesz, és ennek a dürisztornak az árama emiatt tovább fog csökkenni. A 2. dürisztorban épp fordítva, a kicsit megnőtt áram miatt $\displaystyle U_{r2}<U_\mathrm{D0}$, a tekercs feszültsége pozitívvá válik, és így ennek a dürisztornak az árama tovább fog nőni. (A karakterisztika középpontos szimmetriája miatt a változások ellentétes előjelűek, de azonos nagyságúak lesznek, így az összáram valóban nem változik.) Az áramok így kezdetben egyre gyorsulva változnak.

Amikor az egyes dürisztorokban lévő ellenállásokon eső feszültség eléri a lokális szélsőértékeket ($\displaystyle I_\mathrm{D1}\approx 1{,}4\,\mathrm{A}$, illetve $\displaystyle I_\mathrm{D2}\approx 2{,}6\,\mathrm{A}$), akkor a feszültségek változási iránya megfordul, a tekercseken eső feszültségek előjele megmarad, de nagyságuk csökkenni kezd, és így az áramok egyre lassabban változnak. A folyamat akkor ér véget, amikor $\displaystyle I_\mathrm{D1}=1\,\mathrm{A}$ és $\displaystyle I_\mathrm{D2}=3\,\mathrm{A}$ lesz. Az áramok időfüggése az 5. ábrán látható. (A pontos görbealak és az időskála függ a zavar időpontjától és nagyságától, most is csak numerikus számítással kapható meg. A görbe jellege a megfontolások alapján ismét felvázolható.)

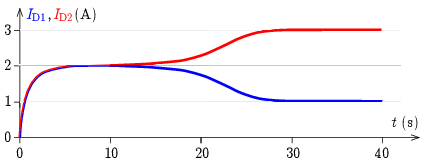
5. ábra

Láthattuk, hogy az azonos áramú egyensúly instabil, hiszen egy kis zavar hatására egyre gyorsulva távolodtak attól az értéktől az áramok. A rendszer az árammentes állapotból először mégis oda tart, mert ez az állapot a szimmetrikus tengely mentén stabil, csak az aszimmetrikus irányban instabil – mint egy nyeregfelület (6. ábra).

Ugyanakkor az aszimmetrikus állapot stabil, amit a következőképp láthatunk be: ha pl. $\displaystyle I_\mathrm{D1}$ kicsit megnő, akkor az 1. dürisztor belső ellenállásán is megnő az áram, a tekercsen negatív feszültség lesz, ami az áramot csökkenti, visszaviszi az egyensúlyi értékre. Ellentétes irányú változásnál (és a másik dürisztoron is) hasonlóan negatív visszacsatolás alakul ki, ami stabilitást eredményez.

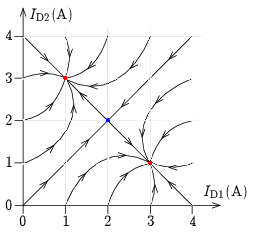
6. ábra

Megjegyzések. 1. A tényleges görbék numerikus módszerekkel könnyen megrajzolhatók. (Erről lásd lapunk novemberi számában Csóka Péter és Seprődi Barnabás: Fizika problémák megoldása numerikus módszerrel című cikkét.) Ehhez a grafikusan megadott karakterisztikára ez a harmadfokú polinom illeszthető ($\displaystyle I_\mathrm{D}$ amperben, $\displaystyle U_r$ voltban):

$\displaystyle U_r=\frac{1}{3}I_\mathrm{D}^3-2I_\mathrm{D}^2+\frac{11}{3}I_\mathrm{D}.$

A numerikus megoldáshoz a következő összefüggéseket írhatjuk fel:

A második szakasz időbeli lefutása függ a kis zavar nagyságától (minél nagyobb a zavar, annál gyorsabban történik). Az 5. ábrán látható grafikon $\displaystyle \Delta t=0{,}1\,\mathrm{s}$ lépéssel, és egy $\displaystyle t=10\,\mathrm{s}$ időpillanatban alkalmazott $\displaystyle \Delta I_\mathrm{D}=\pm 0{,}01\,\mathrm{A}$ nagyságú zavarral készült.

2. Ha a rendszerbe beépítünk egy kicsiny véletlen zajt (és az nem túl nagy), a folyamat első része meglepő módon ugyanúgy végbemegy, a rendszer először (jó közelítéssel) megállapodik az instabil egyensúlyban, majd (a véletlen zaj amplitúdójától – és a véletlentől – függő idő után) elkezd onnan távolodni, hogy aztán végleg (jó közelítéssel) megállapodjon a stabil állapotban. Természetesen ilyenkor véletlenszerűen egyik vagy másik dürisztor árama csökken, illetve nő.

Statisztika:

7 dolgozat érkezett.
6 pontot kapott:	Fajszi Karsa.
5 pontot kapott:	Beke Márton Csaba, Erdélyi Dominik.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2024. decemberi fizika feladatai