A P. 5616. feladat (2025. január)

P. 5616. Egy róka állandó $\displaystyle v_1$ sebességgel, egyenes vonal mentén fut. Üldözőbe veszi őt egy kutya, amelynek sebessége állandó $\displaystyle v_2$ nagyságú, iránya pedig mindig a róka felé mutat. Egy adott pillanatban, amikor a róka és a kutya távolsága $\displaystyle d$, a két sebesség éppen egymásra merőleges. Mekkora a kutya gyorsulása ebben a pillanatban?

Közli: Baranyai Klára, Veresegyház

(5 pont)

A beküldési határidő 2025. február 17-én LEJÁRT.

Megoldás. Mivel a kutya sebességének nagysága nem változik, a gyorsulás csak a sebesség irányának a változásával van összefüggésben (ebből következően csak a pillanatnyi sebesség irányára merőleges lehet).

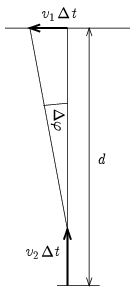
Ahogy az ábráról leolvasható, az adott pillanatot követő igen kicsiny $\displaystyle \Delta t$ idő alatt a kutya futásának az iránya

$\displaystyle \Delta\varphi\cong\frac{v_1\Delta t}{d-v_2\Delta t}\cong\frac{v_1\Delta t}{d}$

szöggel fordul el. (Itt a jelölt közelítő egyenlőségek annál pontosabban teljesülnek, minél kisebb a $\displaystyle \Delta t$ időtartam.) A sebesség megváltozása tehát

$\displaystyle \Delta v_2\cong v_2\Delta\varphi=\frac{v_1v_2\Delta t}{d},$

amiből

$\displaystyle a=\frac{\Delta v_2}{\Delta t}=\frac{v_1v_2}{d}.$

Statisztika:

34 dolgozat érkezett.
5 pontot kapott:	Bálint Áron, Beke Márton Csaba, Csiszár András, Erdélyi Dominik, Gyenes Károly, Klement Tamás, Masa Barnabás, Papp Emese Petra, Pázmándi József Áron, Simon János Dániel, Sipos Márton, Tóth Hanga Katalin, Ujpál Bálint.
4 pontot kapott:	Bencze Mátyás, Kis Boglárka 08, Magyar Levente Árpád, Molnár Lili, Sütő Áron, Tóthpál-Demeter Márk, Ujvári Sarolta, Zámbó Luca, Zólomy Csanád Zsolt.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. januári fizika feladatai