A P. 5622. feladat (2025. január)

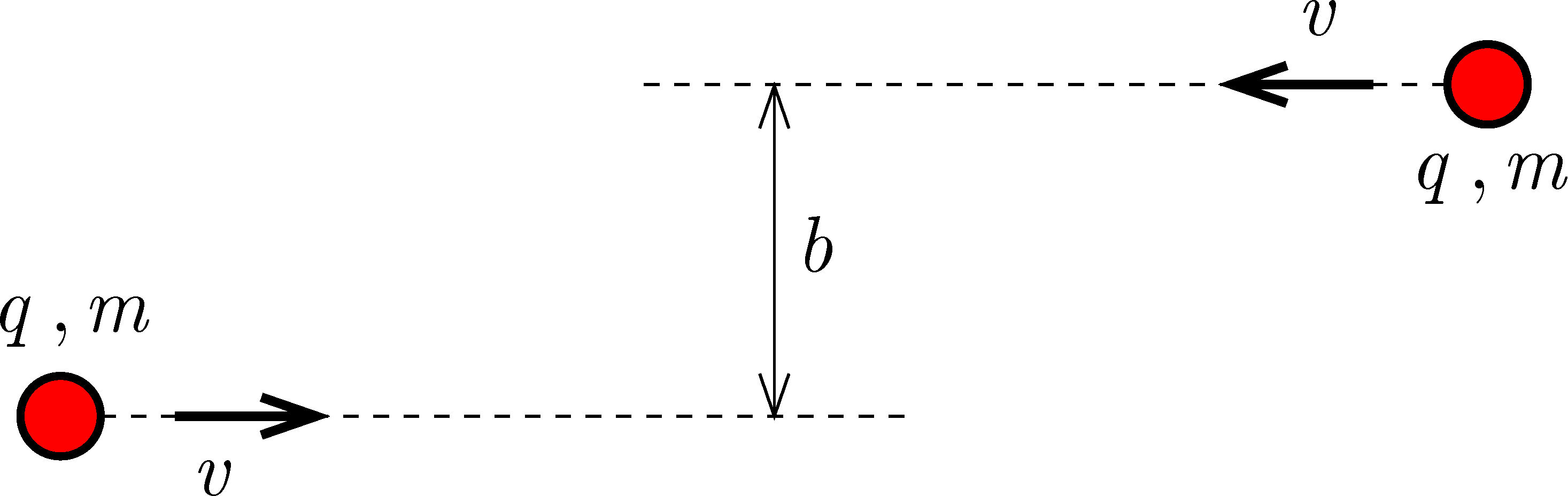
P. 5622. Vízszintes, súrlódásmentes, szigetelő asztallapon egymástól távol két $\displaystyle q$ töltésű, $\displaystyle m$ tömegű, kis méretű, szigetelő korong található. Kezdetben ellentétes irányú, $\displaystyle v$ nagyságú sebességgel mozogva közelednek. Ha nem lenne töltésük, az ábra szerinti, egymástól $\displaystyle b$ távolságra lévő egyenesek mentén mozognának. Mekkora lesz a mozgás során a két korong minimális sebessége?

Közli: Németh Róbert, Budapest

(5 pont)

A beküldési határidő 2025. február 17-én LEJÁRT.

Megoldás: Mivel a két töltésből álló rendszerben csak belső erők hatnak, a teljes lendület időben állandó, azaz mindvégig zérus. Ezzel ekvivalens tulajdonság, hogy a rendszer tömegközéppontja végig mozdulatlan. A Coulomb-erők centrálisak is, így minden pillanatban a tömegközépponttól elfele mutatnak, és eredő forgatónyomatékot nem fejtenek ki. Ez pedig már implikálja a perdület megmaradását.

Jelölje a keresett minimális sebességet $\displaystyle u$, a testek távolságát ennek elérésekor pedig $\displaystyle d$. A szélsőérték-tulajdonság következménye, hogy ebben a pillanatban a testek sebessége merőleges az őket összekötő szakaszra, így a perdületmegmaradás alakja:

$\displaystyle mvb=mud.$

Teljesül emellett az energiamegmaradás törvénye is:

$\displaystyle 2\cdot\frac{1}{2}mv^2=2\cdot\frac{1}{2}mu^2+\frac{kq^2}{d}.$

Az egyenletekből $\displaystyle d$ kiküszöbölhető, az eredmény egy másodfokú egyenlet az $\displaystyle u$ változóra:

$\displaystyle u^2+\frac{kq^2}{mvb}u-v^2=0.$

A fizikailag releváns pozitív megoldásból adódik a végeredmény:

$\displaystyle u=\sqrt{v^2+\left(\frac{kq^2}{2mvb}\right)^2}-\frac{kq^2}{2mvb}.$

Statisztika:

15 dolgozat érkezett.
5 pontot kapott:	Beke Márton Csaba, Erdélyi Dominik, Gyenes Károly, Kovács Tamás, Simon János Dániel, Tóth Hanga Katalin, Tóthpál-Demeter Márk, Ujpál Bálint.
4 pontot kapott:	Ujvári Sarolta.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. januári fizika feladatai