A P. 5625. feladat (2025. február)

P. 5625. Egy lovardában a lovas $\displaystyle 20~\mathrm{m}$ sugarú körön állandó, $\displaystyle 5~\mathrm{m}/\mathrm{s}$ nagyságú sebességgel jár körbe-körbe. A körben áll a lovászmester, a kör közepétől $\displaystyle 10~\mathrm{m}$ távolságra. Mikor változik leglassabban, illetve leggyorsabban a lovas és a lovászmester közötti távolság? Mekkora sebességgel változik a közöttük lévő távolság ebben a két esetben?

Közli: Baranyai Klára, Veresegyház

(5 pont)

A beküldési határidő 2025. március 17-én LEJÁRT.

I. megoldás. Ha a lovas a legközelebb vagy a legtávolabb van a lovászmestertől, akkor éppen nem változik a közöttük lévő távolság. A kérdésre az a válasz, hogy akkor változik a leglassabban a lovas és a lovászmester közötti távolság, amikor a lovas éppen a legközelebbi ponton halad át, vagy éppen a legtávolabbi pont közelében mozog a 20 m sugarú pályáján. Ekkor a lovas és a lovászmester közötti távolság 10 m, illetve 30 m, a távolság állandósága miatt annak változási sebessége nulla.

Az ábrán kétféle nézőpontból láthatjuk a helyzetet. A bal oldali ábrán a talajhoz rögzített rendszerben a lovászmester (M) áll, a lovas (L) pedig 5 m/s kerületi sebességgel 20 m sugarú körpályán mozog. A jobb oldali ábrán lévő forgó rendszerben a lovas áll, és a lovászmester végez 10 m sugarú körön körmozgást ugyanazon középpont körül, 2,5 m/s nagyságú sebességgel, ellenkező körüljárás szerint.

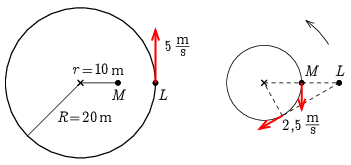
A jobb oldali ábráról leolvashatjuk, hogy akkor nő a leggyorsabban a lovas és a lovászmester közötti távolság, ha a lovászmester sebességének hatásvonalán helyezkedik el a lovas, ami éppen $\displaystyle 60^\circ$-os elfordulási szögnél következik be. Álló rendszerből ez ugyanakkora szögű, pozitív elfordulást jelent. Az ábráról leolvashatjuk azt is, hogy ebben a helyzetben a távolság növekedésének maximális üteme 2,5 m/s.

Ha a jobb oldali ábra félszabályos háromszögét tükrözzük az átfogóra, akkor azt a pontot kapjuk meg, ahol a leggyorsabban csökken a lovas és a lovászmester közötti távolság. A távolság csökkenési sebessége ilyenkor is 2,5 m/s.

II. megoldás Az előző megoldás jelöléseit kiegészítve legyen a lovas kerületi sebessége $\displaystyle u$, a lovas $\displaystyle L$ pozícióját a lovászmester $\displaystyle M$ pozíciójával összekötő szakasz $\displaystyle d$, a kör középpontja pedig $\displaystyle O$!

Nyilván akkor változik $\displaystyle d$ a leggyorsabban, ha $\displaystyle u$-nak $\displaystyle d$ irányára vett

$\displaystyle v=u\sin{\alpha}$

vetülete a legnagyobb. A merőleges szárú szögek egyenlősége miatt $\displaystyle \alpha$ egyenlő az $\displaystyle OLM\triangle$ $\displaystyle L$-nél lévő szögével. Ebben a háromszögben a szinusz-tétel szerint

$\displaystyle \sin{\alpha}=\frac{r}{R}\sin{\delta},$

ami akkor maximális, ha $\displaystyle \sin{\delta}=1$, azaz $\displaystyle \delta=\tfrac{\pi}{2}=90^\circ$. Ekkor $\displaystyle \alpha=\tfrac{\pi}{6}=30^\circ$, ami a lovas $\displaystyle \tfrac{\pi}{3}=60^\circ$-os elfordulásakor következik be. Ilyenkor

$\displaystyle v_\mathrm{max}=\frac{r}{R}u= 2{,}5\,\mathrm{\frac{m}{s}},$

és $\displaystyle d$ növekszik. Azt a pozíciót, amikor a $\displaystyle d$ leggyorsabban csökken, a lovas megfelelő helyzetének az $\displaystyle OM$ szakasz által kitűzött egyenesre való tükrözésével kapjuk meg.

III. megoldás. Jelöljük a lovas és a lovászmester közötti távolságot $\displaystyle d$-vel, a távolság változási sebességét $\displaystyle v$-vel, a sebességváltozás ütemét (vagyis $\displaystyle d$ gyorsulását) $\displaystyle a$-val. Legyen a lovászmesterhez legközelebbi helyzethez képest a lovas (radiánokban mért) szögelfordulása $\displaystyle \varphi$. Ha a távolságokat méter, az időt másodperc egységekben mérjük, akkor $\displaystyle \varphi=t/4$.

A koszinusztétel alapján

ennek az egyenletnek a deriválásából pedig

vagyis

A lovas és a lovászmester közötti távolság akkor változik a leglassabban, amikor a változás pillanatnyi sebessége nulla. (3) szerint ez $\displaystyle t=0$ és $\displaystyle t=4\pi$ időpontokban, vagyis a $\displaystyle \varphi=0$, valamint $\displaystyle \varphi=\pi$ (és azoktól $\displaystyle 2\pi$ egész számú többszörösével eltérő) szögeknél következik be, ekkor kerül a lovas a legközelebb, illetve legtávolabb a lovászmestertől.

A távolság változási sebességének abszolút értéke akkor a legnagyobb, amikor $\displaystyle v$ maximális, illetve minimális értékű. Mindkét esetben $\displaystyle v(t)$ változási sebessége (idő szerinti deriváltja), vagyis az $\displaystyle a$ gyorsulás nulla.

(2) ismételt deriválásával,

$\displaystyle 2ad+2v^2=25\,\cos(t/4),$

ahonnan (3), valamint $\displaystyle a=0$ felhasználásával kapjuk:

$\displaystyle 2\frac{50^2\,\sin^2(t/4)}{500-400\, \cos(t/4)}=25\,\cos(t/4).$

Ebből következik:

Bevezetve a $\displaystyle \xi=\cos(t/4)$ jelölést (4) másodfokú egyenletté alakul:

$\displaystyle \xi^2-\frac{5}{2}\xi+1=0.$

Ennek $\displaystyle \vert\xi\vert\le1$ megoldása:

$\displaystyle \xi=\frac{1}{2},\qquad \varphi=\frac{t}{4}=\pm\frac{\pi}{3}.$

Mindkét esetben (3) szerint $\displaystyle \vert v\vert=2{,}5\,\mathrm{m/s}$. Ekkora sebességgel növekszik a $\displaystyle d$ távolság akkor, amikor a lovas a teljes kör 1/6-át tette meg, a körpálya 5/6 részénél pedig ekkora sebességgel csökken a lovas és a lovászmester közötti távolság.

Statisztika:

30 dolgozat érkezett.
5 pontot kapott:	Bálint Áron, Beke Márton Csaba, Bencze Mátyás, Erdélyi Dominik, Erős Fanni, Gyenes Károly, Kis Boglárka 08, Kovács Tamás, Magyar Zsófia, Molnár Lili, Simon János Dániel, Tóth Hanga Katalin, Vincze Anna.
4 pontot kapott:	Bélteki Teó, Magyar Levente Árpád, Sütő Áron.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. februári fizika feladatai