A P. 5628. feladat (2025. február)

P. 5628. Egy homogén rúdnak tekinthető ceruzát a radíros végével asztallapra támasztunk, és az eldőlését a hegyéhez erősített, a ceruzára merőleges cérnaszállal akadályozzuk meg.

a) Legalább mekkora a radír és az asztallap közötti tapadási súrlódási együttható, ha a ceruza nem csúszik meg, amikor $\displaystyle 15^\circ$-os szöget zár be a függőlegessel?

b) Mekkora súrlódási együttható esetén ,,fektethető le'' lassan a ceruza az asztalra anélkül, hogy az alsó vége megcsúszna, ha a cérnaszál mindvégig merőleges a ceruzára?

Közli: Szentivánszki Soma, Budapest

(5 pont)

A beküldési határidő 2025. március 17-én LEJÁRT.

I. megoldás. Jelöljük a ceruza hosszát $\displaystyle \ell$-lel, a súlyát $\displaystyle G$-vel, a függőlegessel bezárt szögét pedig $\displaystyle \varphi$-vel (1. ábra).

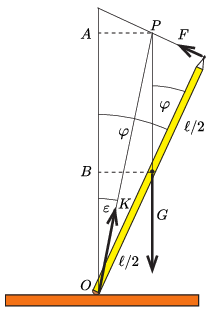
1. ábra

A ceruzára merőleges cérnaszál által kifejtett $\displaystyle F$ erő hatásvonala és a függőleges irányú nehézségi erő hatásvonala a $\displaystyle P$ pontban metszi egymást, tehát egyiküknek sincs forgatónyomatéka erre a pontra vonatkoztatva. A ceruzára a radíros végénél hat még az asztallap valamekkora $\displaystyle K$ erővel, aminek hatásvonala ugyancsak áthalad a $\displaystyle P$ ponton, csak így teljesül a forgatónyomatékok egyensúlyának feltétele.

Jelöljük a $\displaystyle \boldsymbol{K}$ erő hatásvonalának a függőlegessel bezárt szögét $\displaystyle \varepsilon$-nal. A ceruza akkor nem csúszik meg az asztallapon, ha a tapadó súrlódás együtthatója legalább $\displaystyle \tg\varepsilon$.

Megjegyzés. A $\displaystyle \boldsymbol{K}$ erő függőleges komponensét $\displaystyle N$ nyomóerőnek, a vízszintes komponensét $\displaystyle S$ súrlódási erőnek szokták nevezni. Mivel $\displaystyle N=K\cos\varepsilon$ és $\displaystyle S=K\sin\varepsilon$, a tapadási súrlódás $\displaystyle S\le\mu N$ feltétele valóban $\displaystyle \tg\varepsilon\le\mu$ esetén teljesül.

Az 1. ábráról leolvasható, hogy

$\displaystyle AP=\frac{\ell}{2}\sin\varphi,$

$\displaystyle AB=\frac{\ell}{2\cos\varphi},$

$\displaystyle OB=\frac{\ell}{2}\cos\varphi,$

tehát

$\displaystyle \tg\varepsilon=\frac{AP}{AB+OB}=\frac{\sin\varphi\,\cos\varphi}{1+\cos^2\varphi}\equiv f(\varphi).$

a) Adott $\displaystyle \varphi$ szögnél a ceruza egyensúlyának feltétele: $\displaystyle \mu\ge f(\varphi)$. Mivel $\displaystyle \varphi_1=15^\circ$-nál $\displaystyle f(\varphi_1)\approx 0{,}13$, legalább ekkora tapadási súrlódási együttható szükséges a radír és az asztallap között, hogy a ceruza ne csússzon meg.

b) Ha a ceruzát függőleges helyzetéből a cérnaszálnál fogva lassan engedjük megdőlni, a radír elcsúszása akkor kerülhető el, ha minden $\displaystyle 0\le\varphi\le 90^\circ$ szögnél teljesül a $\displaystyle \mu\ge f(\varphi)$ feltétel. Ha az $\displaystyle f(\varphi)$ függvény a legnagyobb értékét valamekkora $\displaystyle \varphi_0$ szögnél veszi fel és $\displaystyle f(\varphi_0)=f_\mathrm{max}$, akkor a ceruza csúszásmentes eldönthetőségének feltétele: $\displaystyle \mu\ge f_\mathrm{max}$.

Határozzuk meg $\displaystyle f(\varphi)$ legnagyobb értékét! Bevezetve az $\displaystyle x=\tg\varphi$ jelölést, $\displaystyle f(\varphi)$ helyett vizsgálhatjuk az

$\displaystyle f(x)=\frac{x}{2+x^2}$

kifejezést, kereshetjük ennek legnagyobb értékét, vagy ami ezzel egyenértékű, kereshetjük

$\displaystyle \frac{1}{f(x)}=\frac{2}{x}+x$

minimális értékét. Ez a számtani és a mértani középértékekre vonatkozó egyenlőtlenségből könnyen megkapható:

$\displaystyle \frac{2}{x}+x=2\cdot\frac{\frac{2}{x}+x}{2}\ge 2\cdot\sqrt{\frac{2}{x}\cdot x}=\sqrt{8}.$

Ezek szerint a kérdésre adható válasz:

$\displaystyle \mu\ge \frac{1}{\sqrt{8}}\approx 0{,}35$

súrlódási együttható esetén ,,fektethető le'' a ceruza az asztalra anélkül, hogy a radíros vége elcsúszna.

Ugyanez az eredmény úgy is megkapható, hogy az $\displaystyle f(\varphi)$ függvény szélsőértékét a deriváltja eltűnéséből határozzuk meg:

$\displaystyle f'(\varphi)=\left.\frac{(\cos^2\varphi-\sin^2\varphi)(1+\cos^2\varphi)+2\sin^2\varphi\cos^2\varphi}{(1+\cos^2\varphi)^2}\right|_{\varphi=\varphi_0} =0,$

ahonnan

$\displaystyle \varphi_0=\arccos\frac{1}{\sqrt{3}}\approx 55^\circ\qquad\textrm{és}\qquad f_\mathrm{max}=f(\varphi_0)=\frac{1}{\sqrt{8}}.$

Az $\displaystyle f(\varphi)$ függvény grafikonját ábrázolva (lásd a 2. ábrát) arról is leolvashatjuk a $\displaystyle 15^\circ$-os dőlésszöghöz tartozó kritikus súrlódási együttható értékét, illetve a függvény maximumhelyét és legnagyobb értékét.

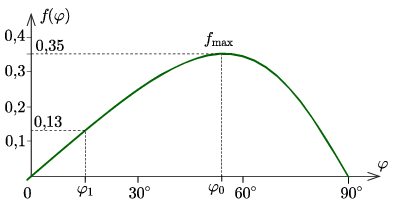
2. ábra

II. megoldás. A (3. ábra) jelöléseivel a ceruza egyensúlyának feltétele:

$\displaystyle N+F\sin\varphi-G=0,$

$\displaystyle S-F\cos\varphi=0,$

$\displaystyle G\,\frac{\ell}{2}\sin\varphi-F\ell=0.$

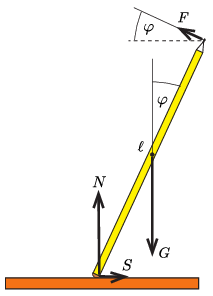
3. ábra

Innen $\displaystyle F$ kiküszöbölése után kapjuk, hogy

$\displaystyle S=\frac12 G \sin\varphi\,\cos\varphi,$

$\displaystyle N=G\left(1-\frac12\sin^2\varphi\right).$

A ceruza radírgumis vége akkor nem csúszik meg az asztallapon, ha

$\displaystyle \mu\ge \frac{S}{N}= \frac{\sin\varphi\,\cos\varphi}{1+\cos^2\varphi}\equiv f(\varphi).$

A megoldás további része megegyezik az I. megoldásnál leírtakkal.

Statisztika:

33 dolgozat érkezett.
5 pontot kapott:	Beke Márton Csaba, Bélteki Teó, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Csiszár András, Erdélyi Dominik, Gyenes Károly, Kiss 131 Adorján Timon, Masa Barnabás, Papp Emese Petra, Simon János Dániel, Sipos Márton, Sütő Áron, Tóth Hanga Katalin.
4 pontot kapott:	Kovács Tamás, Misik Balázs, Monok Péter.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. februári fizika feladatai