A P. 5634. feladat (2025. március)

P. 5634. Egy rajztábla és egy rajta nyugvó könyv között a súrlódási együttható $\displaystyle \mu$. A rajztábla egyik szélét lassan emeljük.

a) Mekkora $\displaystyle \alpha$ hajlásszög esetén csúszik meg a könyv?

b) Mekkora a tábla $\displaystyle 2\alpha$ hajlásszögű helyzetében a lecsúszó könyv gyorsulása?

c) Mekkora az a legkisebb vízszintes gyorsulás, amivel a $\displaystyle 2\alpha$ hajlásszögű táblát előre kellene tolni ahhoz, hogy a könyv ne csússzon meg?

A csúszási és a tapadási súrlódási együtthatót tekintsük egyenlőnek. Az eredményeket $\displaystyle \mu$ és $\displaystyle g$ segítségével adjuk meg.

Közli: Honyek Gyula, Veresegyház

(5 pont)

A beküldési határidő 2025. április 15-én LEJÁRT.

I. megoldás. A megcsúszás határán a nyomóerő és a súrlódási erő eredője a felület normálisával $\displaystyle \varepsilon$ szöget zár be, ez a megcsúszás határszöge. Mivel a súrlódási erő nagysága ekkor éppen a nyomóerő nagyságának $\displaystyle \mu$-szöröse, és a két erő merőleges egymásra, $\displaystyle \tg\varepsilon=\mu$.

a) A könyvre a nehézségi erő és a rajztábla felülete által kifejtett kényszererő hat (1. ábra). A két erő csak akkor lehet egyensúlyban, ha irányuk (és nagyságuk) megegyezik. Ez alapján:

$\displaystyle \alpha=\varepsilon=\arctg\mu.$

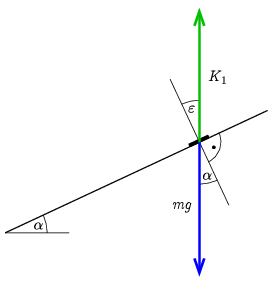
1. ábra

b) A könyvre most is csak a nehézségi erő és a kényszererő hat (amelynek a nagysága természetesen nem egyezik meg az a) részben szereplővel: akkorának kell lennie, hogy a lejtőre (rajztáblára) merőleges komponense kiegyenlítse a nehézségi erő lejtőre merőleges komponensét). Ezek eredőjének a felülettel párhuzamosnak kell lennie: ez az eredő erő hozza létre a könyv keresett lejtőirányú gyorsulását. A 2. ábrán berajzoltuk a könyvre ható erőket és ezek eredőjét is: ez utóbbi végpontját a kényszererő hatásvonala metszi ki a lejtővel párhuzamos egyenesből. Bejelöltünk szögeket, és megrajzoltunk néhány egyenest: látható, hogy az alul keletkező kis háromszög egyenlőszárú, és így a vízszintes szára is $\displaystyle ma$ hosszúságú. Ezután már az ábráról leolvashatjuk:

$\displaystyle ma=mg\tg\alpha\qquad\Rightarrow\qquad a=g\tg\alpha=\mu g.$

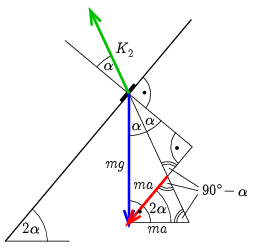
2. ábra

c) A mozgást vizsgáljuk a lejtővel együtt gyorsuló vonatkoztatási rendszerben. Legyen a lejtő minimális gyorsulása $\displaystyle a_0$. Ekkor egy vízszintes, $\displaystyle ma_0$ nagyságú tehetetlenségi erő hatását is figyelembe kell venni (amely a lejtő gyorsulásával ellentétes irányba mutat). Az erőnek akkorának kell lennie, hogy kiegyenlítse a nehézségi erő és a kényszererő eredőjét. A legkisebb ilyen gyorsulást keressük, ezért a kényszererő most is az eddigi, ,,éppen nem csúszik meg lefele'' határhelyzetben van. A 3. ábrán láthatjuk, hogy a kényszererő hatásvonala kimetszi az $\displaystyle ma_0$ erő végpontját (és egyben meghatározza $\displaystyle K_3$ nagyságát is, de arra a feladat megoldásához nincs szükségünk). Az ábráról közvetlenül leolvasható a lejtő keresett legkisebb gyorsulása:

$\displaystyle ma_0=mg\tg\alpha\qquad\Rightarrow\qquad a_0=g\tg\alpha=\mu g.$

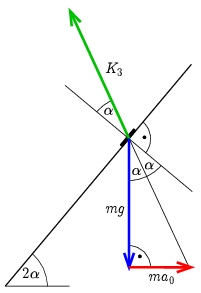
3. ábra

Megjegyzés. A feladatnak csak akkor van értelme, ha $\displaystyle 2\alpha<90^\circ$, és így $\displaystyle \mu<1$.

II. megoldás. a) A könyvre az $\displaystyle mg$ nehézségi erő, a lejtőre merőleges $\displaystyle N$ nyomóerő és a lejtővel párhuzamos $\displaystyle S$ súrlódási erő hat. A könyvre ható erők lejtővel párhuzamos és lejtőre merőleges komponenseinek egyensúlya, valamint a súrlódási erő összefüggése a megcsúszás határesetében:

$$\begin{gather*} mg\cos\alpha=N,\\ mg\sin\alpha=S,\\ S=\mu N. \end{gather*}$$

$\displaystyle S$ kifejezését a harmadik egyenletből a másodikba behelyettesítve, majd az első két egyenletet egymással elosztva:

$\displaystyle \tg\alpha=\mu\qquad\Rightarrow\qquad\alpha=\arctg\mu.$

b) A könyvre ismét három erő hat, ezek hatására a lejtővel párhuzamosan gyorsulni fog. Felírva a lejtőre merőleges komponensek egyensúlyát, a lejtővel párhuzamos mozgásegyenletet és a csúszási súrlódás összefüggését:

$$\begin{gather*} mg\cos 2\alpha=N,\\ ma=mg\sin 2\alpha-S,\\ S=\mu N. \end{gather*}$$

A harmadik egyenletből $\displaystyle S$, majd az első egyenletből $\displaystyle N$ kifejezését beírva a második egyenletbe, és rendezve:

$\displaystyle a=(\sin 2\alpha-\mu\cos 2\alpha)g.$

A trigonometrikus kifejezések átalakítása, ahol felhasználjuk a $\displaystyle \tg\alpha=\mu$ összefüggést is:

$$\begin{gather*} \sin 2\alpha=2\sin\alpha\cos\alpha=2\,\sqrt{\frac{\tg^2\alpha}{1+\tg^2\alpha}}\,\sqrt{\frac{1}{1+\tg^2\alpha}}=\frac{2\tg\alpha}{1+\tg^2\alpha}=\frac{2\mu}{1+\mu^2},\\ \cos 2\alpha=\cos^2\alpha-\sin^2\alpha=\frac{1}{1+\tg^2\alpha}-\frac{\tg^2\alpha}{1+\tg^2\alpha}=\frac{1-\tg^2\alpha}{1+\tg^2\alpha}=\frac{1-\mu^2}{1+\mu^2}. \end{gather*}$$

Ezeket behelyettesítve a keresett gyorsulás:

$\displaystyle a=\left(\frac{2\mu}{1+\mu^2}-\mu\frac{1-\mu^2}{1+\mu^2}\right)g=\mu g.$

c) Vizsgáljuk a mozgást a lejtővel együtt gyorsuló koordináta-rendszerben. Legyen a lejtő gyorsulása $\displaystyle a_0$. Ekkor a könyvre az eddigi három erőn kívül egy vízszintes, $\displaystyle -ma_0$ nagyságú tehetetlenségi erő hatását is figyelembe kell venni. Az egyensúly feltétele az a) részhez hasonlóan:

$$\begin{gather*} mg\cos 2\alpha+ma_0\sin 2\alpha=N,\\ mg\sin 2\alpha=ma_0\cos 2\alpha+S,\\ S=\mu N. \end{gather*}$$

Az egyenletrendszerből $\displaystyle a_0$-t kifejezve, majd a b) részből $\displaystyle \sin 2\alpha$ és $\displaystyle \cos 2\alpha$ kifejezéseit felhasználva, és egyszerűsítve:

$\displaystyle a_0=\frac{\sin 2\alpha-\mu\cos 2\alpha}{\cos 2\alpha+\mu\sin 2\alpha}g=\mu g.$

Megjegyzések. 1. A feladat megoldható inerciarendszerben is: ilyenkor a három erő a könyvet $\displaystyle a_0$ gyorsulással gyorsítja vízszintesen (hogy ne mozogjon a lejtőhöz képest). A mozgásegyenletek:

$$\begin{gather*} mg=N\cos 2\alpha+S\sin 2\alpha,\\ ma_0=N\sin 2\alpha-S\cos 2\alpha,\\ S=\mu N, \end{gather*}$$

amelyből a minimális gyorsulásra ugyanazt az eredményt kapjuk.

2. A feladat a lejtő legkisebb gyorsulását keresi, de meghatározhatjuk a legnagyobb gyorsulást is, amely esetében a könyv nem csúszik meg. Ekkor a súrlódási erő nagysága szintén maximális, de iránya ellentétes (hiszen azt kell megakadályoznia, hogy a könyv felfelé megcsússzon). Ekkor az egyensúly feltétele (a lejtővel együtt gyorsuló vonatkoztatási rendszerben):

$$\begin{gather*} mg\cos 2\alpha+ma_0'\sin 2\alpha=N,\\ mg\sin 2\alpha+S=ma_0'\cos 2\alpha,\\ S=\mu N, \end{gather*}$$

amiből

$\displaystyle a_0'=\frac{\sin 2\alpha+\mu\cos 2\alpha}{\cos 2\alpha-\mu\sin 2\alpha}g=\frac{\mu(3-\mu^2)}{1-3\mu^2}g.$

A képlet $\displaystyle \mu>\tfrac{1}{\sqrt{3}}$ esetben negatív értéket ad, de ez hibás eredmény, mert a tapadó súrlódás nem tudja elindítani a könyvet – ilyenkor a súrlódási erő nagysága kisebb lesz a maximális értéknél. Ezt el lehetett volna kerülni, ha az egyenletrendszer harmadik egyenlete helyett egyenlőtlenséget írunk: $\displaystyle 0\leq S\leq\mu N$.

Látható, ha $\displaystyle \mu\geq\tfrac{1}{\sqrt{3}}$ (azaz $\displaystyle \alpha\geq 30^\circ$, $\displaystyle 2\alpha\geq 60^\circ$), akkor a gyorsulás végtelen nagy lehet, a könyv ,,befeszül'', ,,rátapad'' a lejtőre.

Statisztika:

A P. 5634. feladat értékelése még nem fejeződött be.

A KöMaL 2025. márciusi fizika feladatai

Már regisztráltál?
Új vendég vagy?