A P. 5635. feladat (2025. március)

P. 5635. A nyújtón az óriáskör bemutatásánál a tornász éppen átbillen a felső függőleges helyzetén. Amikor alulra ér, az acélrúd láthatóan meghajlik. Modellezzük a tornászt egy vékony, súlyos, homogén rúddal, ami vízszintes tengely körül forog. Ha a rúd a felső állásából az alsóba ér, akkor a súlyának hányszorosával húzza a tengelyt? (A súrlódást, közegellenállást, a tengely behajlását a rúd hosszához képest hanyagoljuk el.)

Közli: Gelencsér Jenő, Kaposvár

(4 pont)

A beküldési határidő 2025. április 15-én LEJÁRT.

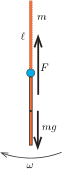
Megoldás. Jelöljük a tornászt modellező rúd tömegét $\displaystyle m$-mel, hosszát $\displaystyle \ell$-lel. Egy ilyen rúdnak a végpontján átmenő, rá merőleges tengelyre vonatkoztatott tehetetlenségi nyomatéka $\displaystyle \Theta=\tfrac{1}{3}m\ell^2.$

Miközben a rúd a felső állásból az alsóba ér, a tömegközéppontja $\displaystyle \ell$ távolsággal mélyebbre kerül, tehát a helyzeti energiája $\displaystyle mg\ell$-lel csökken. Ha a kezdetben álló rúd szögsebessége a legmélyebb helyzetben $\displaystyle \omega$ lesz, akkor a mozgási energiája $\displaystyle \frac{1}{2}\Theta\omega^2$-tel növekszik.

Elhanyagolható súrlódás és közegellenállás esetén alkalmazható a mechanikai energia megmaradásának tétele:

$\displaystyle mg\ell=\frac{1}{2}\left(\frac{1}{3}m\ell^2\right)\omega^2,$

vagyis a rúd maximális szögsebessége:

$\displaystyle \omega=\sqrt{\frac{6g}{\ell}}.$

A rúd alsó helyzetében a rúd tömegközéppontja

$\displaystyle v=\frac{1}{2}\ell\omega=\sqrt{\frac{3}{2}g\ell}$

sebességgel $\displaystyle \ell/2$ sugarú körpályán mozog, így a gyorsulása függőlegesen felfelé

$\displaystyle a=\frac{v^2}{\ell/2}=3g.$

A rúd tömegközéppontjára felírható mozgásegyenlet:

$\displaystyle F-mg=ma,$

ahonnan a tengely által kifejtett erő:

$\displaystyle F=4mg.$

Ennek az erőnek az ellenereje a nyújtó tengelyére ható, függőlegesen lefelé irányuló, $\displaystyle 4mg$ nagyságú erő, ez okozza a nyújtó rúdjának lehajlását.

Statisztika:

41 dolgozat érkezett.
4 pontot kapott:	Bélteki Teó, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Csiszár András, Éliás Kristóf , Fekete Lúcia, Kis Boglárka 08, Misik Balázs, Molnár Lili, Papp Emese Petra, Páternoszter Tamás, Sütő Áron, Tóth-Tűri Bence, Ujpál Bálint, Vértesi Janka, Vincze Anna, Zámbó Luca.
3 pontot kapott:	Balázs Barnabás, Hajdu Eszter, Hornok Máté, Kávai Ádám, Kovács Tamás, Magyar Zsófia, Masa Barnabás, Monok Péter, Nagy Gellért Ákos, Pituk Péter, Sárecz Bence, Szécsi Bence, Tóth Bertalan, Ujvári Sarolta, Varga 802 Zsolt.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. márciusi fizika feladatai