A P. 5639. feladat (2025. március)

P. 5639. A mellékelt kapcsolási rajznak megfelelően összeállított áramkörben a feszültségforrás elektromotoros ereje $\displaystyle 6~\mathrm{V}$, belső ellenállásának nagysága $\displaystyle 2~\Omega$. Az ideális tekercs önindukciós együtthatója $\displaystyle 1{,}5~\mathrm{H}$, az $\displaystyle R$ ellenállás pedig $\displaystyle 1000~\Omega$ nagyságú. Kezdetben a kapcsoló zárva van.

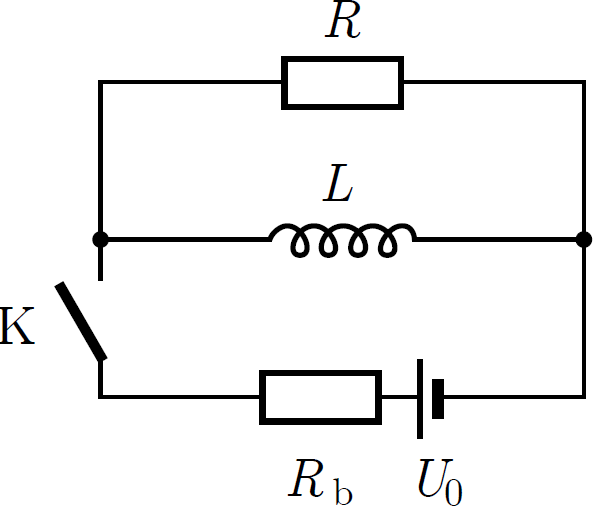
a) Mekkora töltés áramlik át az $\displaystyle R$ ellenálláson a kapcsoló kinyitása után?

b) Mennyi hő fejlődik az $\displaystyle R$ ellenálláson ezalatt?

Tornyai Sándor fizikaverseny nyomán, Hódmezővásárhely

(5 pont)

A beküldési határidő 2025. április 15-én LEJÁRT.

Megoldás. Amíg a kapcsoló zárva van az $\displaystyle R$ ellenálláson nem folyik áram (olyan, mintha ott se lenne), hiszen az ,,ideális'' tekercs ellenállása (időben állandó áram esetében) elhanyagolható. A tekercsen átfolyó áram (1. ábra):

$\displaystyle I_0=\frac{U_0}{R_\mathrm{b}}=3\,\mathrm{A}.$

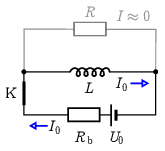
1. ábra

A kapcsoló kinyitása ($\displaystyle t=0$) után a tekercs árama nem változhat ugrásszerűen, így az $\displaystyle R$ ellenálláson $\displaystyle I(0)=I_0=3\,\mathrm{A}$ áram kezd folyni, és $\displaystyle U(0)=RI(0)=RI_0=3000\,\mathrm{V}$ feszültség fog esni. Ugyanekkora nagyságú – de a rajta átfolyó áram irányához viszonyítva ellentétes irányú – a tekercs feszültsége is (2. ábra).

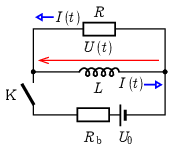
2. ábra

Ebből meghatározhatjuk az áram változási sebességét:

Ez egy időben exponenciálisan lecsengő áramot ír le, de a függvény meghatározására nincsen szükségünk. Az egyenletet szorozzuk át $\displaystyle -\tfrac{L}{R}$-rel és formálisan $\displaystyle \mathrm{d}t$-vel, így megkapjuk, mekkora töltés áramlik át egy kicsiny $\displaystyle \mathrm{d}t$ idő alatt:

$\displaystyle \mathrm{d}q=I(t)\mathrm{d}t=-\frac{L}{R}\mathrm{d}I.$

Ebből egyszerű összegzéssel megkapjuk a lecsengési folyamat során átáramló össztöltést:

$\displaystyle q=\sum\mathrm{d}q=\sum_0^\infty I(t)\mathrm{d}t=-\frac{L}{R}\sum_0^\infty\mathrm{d}I=-\frac{L}{R}(-I_0)=\frac{L}{R}I_0=\frac{L}{R}\frac{U_0}{R_\mathrm{b}}=4{,}5\,\mathrm{mC}.$

Megjegyzés. Az áram időfüggésére felírt differenciálegyenletnek jól ismerjük a megoldását (ilyen a radioaktív bomlást leíró összefüggés is):

$\displaystyle I(t)=I_0\mathrm{e}^{-\frac{t}{\tau}},$

ahol

$\displaystyle \tau=\frac{L}{R}=1{,}5\,\mathrm{ms}.$

Ezután az átáramló össztöltést meghatározhatjuk az áram integrálásával a lecsengés teljes ideje alatt:

$\displaystyle q=\int\limits_0^\infty I(t)\mathrm{d}t=\int\limits_0^\infty I_0\mathrm{e}^{-\frac{t}{\tau}}\mathrm{d}t=\left[-\tau I_0\mathrm{e}^{-\frac{t}{\tau}}\right]_0^\infty=\tau I_0=\frac{L}{R}\frac{U_0}{R_\mathrm{b}},$

az előbb kapott eredménnyel összhangban.

A ,,végtelen'' ideig tartó összegzés furcsának tűnik, de valójában a lecsengés az időállandó tízszerese (tehát 15 ezredmásodperc) alatt lényegében lejátszódik.

b) Az ellenálláson annyi hő fejlődik, amekkora a kapcsoló nyitásának pillanatában a tekercs mágneses energiája volt:

$\displaystyle Q=E_\textrm{m}=\frac{1}{2}LI_0^2=6{,}75\,\mathrm{J}.$

Megjegyzés. A hőt megkaphatjuk a változó áram Joule-teljesítményének összegzésével is:

$\displaystyle Q=\int\limits_0^\infty P(t)\mathrm{d}t=\int\limits_0^\infty R\left[I(t)\right]^2\mathrm{d}t=RI_0^2\int\limits_0^\infty \mathrm{e}^{-2\frac{t}{\tau}}\mathrm{d}t=-\frac{\tau}{2}RI_0^2\left[\mathrm{e}^{-2\frac{t}{\tau}}\right]_0^\infty=\frac{\tau}{2}RI_0^2=\frac{1}{2}LI_0^2,$

az előző megoldással összhangban.

Statisztika:

A P. 5639. feladat értékelése még nem fejeződött be.

A KöMaL 2025. márciusi fizika feladatai