 |
A P. 5642. feladat (2025. március) |
P. 5642. Newton már 1679-ben felvetette, hogy a Föld forgását egy mechanikai kísérlettel is bizonyítani lehetne úgy, hogy megmérjük egy szabadon eső kicsiny golyónak a függőlegestől való, keleti irányú eltérülését. Hooke, aki Newton idejében a Royal Society titkára és kiváló kísérletező volt, 1680-ban végzett is ilyen méréseket.
Egy kellően gazdag és ambiciózus egyenlítői országban modern eszközökkel meg akarják ismételni a csaknem 350 évvel korábbi kísérletet. A tervek szerint egy \(\displaystyle 200~\mathrm{m}\) magas, függőleges, légritkított csőben (vákuumtoronyban) fognak kicsiny acélgolyókat viaszlemezre ejteni.
Határozzuk meg az eltérülés nagyságát úgy, hogy a számolást
a) inerciarendszerben,
b) a Földdel együtt forgó (gyorsuló) koordináta-rendszerben
végezzük el!
Közli: Kis Tamás, Heves
(6 pont)
A beküldési határidő 2025. április 15-én LEJÁRT.
I. Megoldsás. a) Jelöljük a Föld sugarát \(\displaystyle R\)-rel, a szögsebességét \(\displaystyle \omega\)-val, a torony magasságát pedig \(\displaystyle h\)-val. Az esés ideje ekkor \(\displaystyle T=\sqrt{\frac{2h}{g}}\), ahol \(\displaystyle g\) a nehézségi gyorsulás nagysága az Egyenlítőnél.
Inerciarendszerből nézve a test kezdősebessége (keleti irányban)
\(\displaystyle v_0=(R+h)\omega.\)
Ha az elejtésétől számított \(\displaystyle t\) idő alatt a test elmozdulása keleti irányban \(\displaystyle x(t)\), akkor a rá ható nehézségi erő vízszintes komponense \(\displaystyle -mg\frac{x}{R}\), és így a vízszintes irányú mozgás dinamikai egyenlete:
\(\displaystyle a_x(t)=-\frac{g}{R}\cdot x(t).\)
Ez a gyorsulás onnan származik, hogy a nehézségi erőtér nem homogén, iránya nem esik egybe a kiindulási ponthoz tartozó függőlegessel. (A nehézségi erő nagyságának változását \(\displaystyle h\ll R\) miatt elhanyagolhatjuk.)
Felismerhetjük, hogy a fenti egyenlet a harmonikus rezgőmozgás mozgásegyenlete, amelynek megoldása \(\displaystyle x(0)=0\) és \(\displaystyle v_0\) kezdőfeltételek mellett
\(\displaystyle x(t)= \sqrt{\frac{R}{g}}(R+h)\omega\sin\sqrt{\frac{g}{R}}t,\)
így a teljes elmozdulás \(\displaystyle T\) idő alatt
\(\displaystyle x_\textrm{test}= \sqrt{\frac{R}{g}}(R+h)\omega\,\sin\sqrt{\frac{g}{R}}T.\)
Mivel \(\displaystyle \varphi\equiv\sqrt{\tfrac{g}{R}}T\ll 1\), alkalmazhatjuk a szinusz függvény
\(\displaystyle \sin\varphi\approx\varphi-\frac{\varphi^3}{6}\)
közelítő formuláját. (Az elsőrendű tagból származó elmozdulást éppen kiejti majd a torony aljának elmozdulása, így a keresett eltérülés a harmadrendű tagból fog származni.) Ezzel kapjuk, hogy
\(\displaystyle x_\textrm{test}\approx(R+h)\left(\omega T-\frac{g\omega T^3}{6R}\right),\)
vagyis \(\displaystyle h=gT^2/2\) felhasználásával és a legkisebb, \(\displaystyle h/R\)-rel arányos tag elhanyagolásával
\(\displaystyle x_\textrm{test}\approx R\omega T+\frac{1}{3}{g\omega T^3.}\)
A jobb oldal első tagja éppen a torony aljának elmozdulása:
\(\displaystyle R\omega T=x_\textrm{torony alja},\)
így a leejtett golyó a torony aljától
\(\displaystyle \Delta x=x_\textrm{test}-x_\textrm{torony alja}=\frac{1}{3}g\omega T^3,\)
ami a megadott toronymagasság esetén kb. 6 cm.
Megjegyzés. Ha nem vennénk figyelembe a nehézségi erő irányának kicsiny változását, akkor a hibás
\(\displaystyle \Delta x=h\omega T=\frac{1}{2}g\omega T^3\approx 9\,\mathrm{cm}\)
,,eredményt'', vagyis a helyes érték másfélszeresét kapnánk.
b) Forgó rendszerben a keleti irányba mutató Coriolis-gyorsulás: \(\displaystyle a_x=2v\omega=2gt\omega\), az ehhez tartozó sebesség: \(\displaystyle v_x=g\omega t^2\), és végül az elmozdulás: \(\displaystyle x=\tfrac{1}{3}g\omega t^3=\tfrac{1}{3}g\omega\left(\sqrt{\tfrac{2h}{g}}\right)^3=\tfrac{2}{3}\omega ht=\tfrac{2}{3}\omega h\sqrt{\tfrac{2h}{g}}\approx 6\,\mathrm{cm}\).
II. Megodás. a) A \(\displaystyle h\) magasságban (az erősen torzított ábrán a \(\displaystyle B\) pontból) elejtett test tulajdonképpen egy olyan ellipszis pályán halad, aminek az egyik fókuszpontja a Föld \(\displaystyle O\) középpontja, a nagytengely egyik végpontja pedig a \(\displaystyle B\) pont. Ez a görbe a \(\displaystyle C\) pontban metszi a földfelszínt. Az esés \(\displaystyle T=\sqrt{2h/g}\) ideje alatt az \(\displaystyle \omega\) szögsebességgel forgó felszín \(\displaystyle A\) pontja az \(\displaystyle A^{\prime}\) pontba kerül. A feladatunk az \(\displaystyle \overline{A^{\prime}C}\) szakasz \(\displaystyle \Delta x\) hosszának a meghatározása.
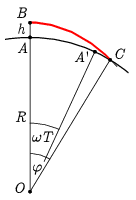
Megjegyzés. Hogy érzékeljük a nagyságrendeket: \(\displaystyle \tfrac{h}{R}\sim 3\cdot 10^{-5}\), vagy \(\displaystyle \omega T\sim\varphi\sim 5\cdot 10^{-4}\,\mathrm{rad}\). Ezeket az arányokat tükröző ábrán nyilván nem látszana semmi, ezért csak erős torzítás árán tudjuk bemutatni a részleteket.
Kepler II. törvénye értelmében az eső test úgy mozog, hogy a vezérsugár területi sebessége állandó. Ez a sebesség
\(\displaystyle (R+h)\frac{v_0}{2}=(R+h)^2\frac{\omega}{2},\)
az \(\displaystyle OBC\) idom területe tehát
\(\displaystyle \mathcal{T}=\frac{1}{2}(R+h)^2\omega T.\)
Ezt a területet a geometria alapján is megadhatjuk:
\(\displaystyle \mathcal{T}=\frac{1}{2}R^2\varphi+\frac{2}{3}hR\varphi.\)
Itt magyarázatra szorul a második tag, amely a \(\displaystyle ABC\) idom területe. A valóságban a \(\displaystyle \varphi\) nagyon kicsiny, ezért az \(\displaystyle AC\) körív egy az \(\displaystyle OB\) tengelyre merőleges egyenesnek tekinthető, másrészt a \(\displaystyle BC\) ellipszis ív egy parabola szakasszal közelíthető, amelyről tudjuk, hogy a \(\displaystyle h\) és \(\displaystyle R\varphi\) oldalú téglalap területét 2/3 : 1/3 arányban osztja.
A két kifejezés
\(\displaystyle \frac{1}{2}R^2\varphi+\frac{2}{3}hR\varphi=\frac{1}{2}(R+h)^2\omega T\)
egyenlőségéből \(\displaystyle \tfrac{h}{R}\)-ben vezető rendig
\(\displaystyle \varphi=\frac{(1+\frac{h}{R})^2}{1+\frac{4h}{3R}}\omega T\cong\left(1+\frac{2}{3}\frac{h}{R}\right)\omega T,\)
ahonnan
\(\displaystyle \Delta x=R\varphi-R\omega T=\frac{2}{3}h\omega T.\)
Statisztika:
A P. 5642. feladat értékelése még nem fejeződött be.
A KöMaL 2025. márciusi fizika feladatai