Az S. 114. feladat (2017. február)

S. 114. A vulkanikus eredetű szigetek gyakran egy vonal mentén helyezkednek el. Egy ilyen szigetcsoport mesés kincset rejt. Kalóz vagy, és hozzájutottál egy térképhez, amelyen az összes sziget rajta van. Mindegyik szigeten van valamennyi kincs, melyeknek a pontos helyét és értékét minden sziget esetén ismered. Legénységet toboroztál és készen állsz a nagy útra, viszont a térkép alapján elkezdtél kételkedni, hogy talán nem minden egyes szigetre érdemes elhajózni, ugyanis a hajózás nagyon megdrágult az utóbbi hónapokban.

Minden sziget esetében ismered, hogy mennyibe kerül odahajózni a kiindulási kikötőből (most itt vagy, ez a szigetcsoporton kívül helyezkedik el), illetve minden pár szomszédos szigetre tudod, hogy mennyibe kerül az út a két sziget között (mindkét irányban ugyanannyi). A kiindulási kikötőből el kell hajóznod az egyik szigetre, ezután a szigetek között tetszőlegesen hajózhatsz. Ezenkívül néhányan megtudták, hogy nálad van a kincses térkép, így irigyek és tudod, hogy bármire képesek lennének, hogy megszerezzék, ezért soha többé nem jöhetsz vissza a kiindulási kikötőbe (vagyis a szigetcsoporton belül akárhol befejezheted az utadat). Ez azt is jelenti, hogy akkor is el kell hajóznod, ha a kincskereső utad veszteséges lenne, ekkor a legkisebb veszteségre kell törekedned. Készíts programot, amely megadja, hogy hogyan hajózz, hogy a legtöbb nyereségre, vagy a legkisebb veszteségre tegyél szert.

A standard bemenet első sorában a szigetek \(\displaystyle N\) száma van. A második sor \(\displaystyle N\) darab nemnegatív egész számot tartalmaz, az \(\displaystyle i\)-edik \(\displaystyle K[i]\), az \(\displaystyle i\)-edik szigeten lévő kincs értéke. A harmadik sor szintén \(\displaystyle N\) darab nemnegatív egész számot tartalmaz, az \(\displaystyle i\)-edik \(\displaystyle H[i]\), a kiindulási kikötőből az \(\displaystyle i\)-edik szigetre hajózás költsége. A negyedik sor \(\displaystyle N-1\) darab nemnegatív egész számot tartalmaz, az \(\displaystyle i\)-edik szám \(\displaystyle S[i]\), az \(\displaystyle i\)-edik és az \(\displaystyle (i+1)\)-edik sziget közötti hajózás költsége.

A standard kimenet első sorába írd ki a maximális hasznot/minimális veszteséget, a második sor tartalmazzon egy maximális hasznot/minimális veszteséget hozó útvonalat: az első szám legyen \(\displaystyle L\), a hajóutak (egy-egy hajóút a kiindulási kikötőből egy szigetre hajózás, valamint a hajóutak száma), ezt kövesse \(\displaystyle L\) sziget sorszáma, a hajóutak célpontjai.

Pontozás: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. 4 pontot ér a maximális haszon/minimális veszteség helyes meghatározása, és további 5 pontot ér a szigetek egy lehetséges, a fenti eredményt adó bejárása. Ha a haszon/veszteség értéke helytelen, akkor a hajóutakért nem jár pont.

Korlátok: \(\displaystyle 1\le N\le 200\,000\), \(\displaystyle 0\le K[i],H[i],S[i]\le 10^9\).

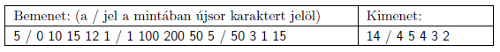
Magyarázat: Az ötödik szigetre hajózunk először (1 kincs – 5 költség), majd sorban jön a 4-es, 3-as, majd a 2-es (rendre \(\displaystyle 12+15+10\) kincs – \(\displaystyle 15+1+3\) költség) összesen \(\displaystyle 38-24=14\) haszon.

Beküldendő egy tömörített s114.zip állományban a program forráskódja és rövid dokumentációja, amely ismerteti a megoldás menetét és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2017. március 10-én LEJÁRT.

Statisztika:

14 dolgozat érkezett.
10 pontot kapott:	Busa 423 Máté, Csenger Géza, Gáspár Attila, Horváth Botond István, Janzer Orsolya Lili, Molnár Bálint, Németh 123 Balázs, Noszály Áron, Tóth 827 Balázs.
9 pontot kapott:	Nagy Nándor.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
3 pontot kapott:	2 versenyző.

A KöMaL 2017. februári informatika feladatai