 |
Az S. 123. feladat (2018. február) |
S. 123. Egy ország sík területen fekszik, minden városa egy képzeletbeli négyzetháló egész koordinátákkal rendelkező csúcsában helyezkedik el. A közlekedési miniszter javaslatára felújítják az úthálózatot úgy, hogy minden városból minden városba el lehessen jutni. A tervek szerint a városok közötti utak az elképzelt négyzetháló élei mentén haladnának, egymással párhuzamosan, vagy egymásra merőlegesen. Az utak egy-egy egész koordinátájú pontban találkozhatnak akár egy városban, akár a városon kívül. A miniszter szeretné a legkisebb költséggel elkészíteni az új úthálózatot, ezért az utak összhosszának a lehető legkevesebbnek kell lennie. Készítsünk programot, amely megadja ezt a legkisebb értéket.
A program standard bemenete az ország városainak N száma, majd a következő N sorban az i-edik város helyének xi és yi egész koordinátái. A program adja meg a standard kimeneten az összeköttetéshez szükséges legrövidebb úthálózat teljes hosszát.
Példa (az újsor karaktereket / jelöli):
| Bemenet | Kimenet |
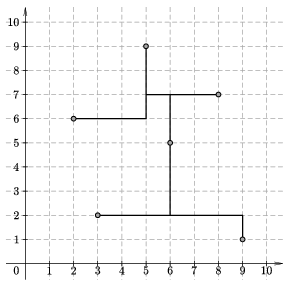
| 6 / 3 2 / 9 1 / 6 5 / 2 6 / 8 7 / 5 9 / | 21 / |
Korlátok: 2≤N≤1000, 1≤xi,yi≤105, egész számok.
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb N érték esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy s123.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
A beküldési határidő 2018. március 12-én LEJÁRT.
Köszönjük Horváth Botond István megjegyzését (chen2002.pdf), a feladatnak valóban nem ismert polinom lépésszámú megoldása. A megoldásokat csak N≤15 bementekre vizsgáltuk.
Mintaként Ürössy Dorottya, 9. évfolyamos budapesti versenyző C#-ban készül megoldását mutatjuk be: Program.cs.
Statisztika:
2 dolgozat érkezett. 10 pontot kapott: Ürmössy Dorottya. 3 pontot kapott: 1 versenyző.
A KöMaL 2018. februári informatika feladatai
|
|

