 |
Az S. 124. feladat (2018. március) |
S. 124. Kertész barátunk telke téglalap alakú, oldalainak hossza \(\displaystyle a\) és \(\displaystyle b\) egység. A kertre terítsünk gondolatban egy egység oldalú négyzethálót. Barátunk szeretné a kert bizonyos részeit egység nagyságú, négyzet alakú járólapokkal lefedni, hogy a kertben utakat hozzon létre. A járólapok a négyzetháló egy-egy négyzetében helyezkednének el. A kert egyik kiválasztott sarkában lenne az első járólap, és a szemközti sarkában az utolsó. A járólapokon szépen át lehetne sétálni az első járólapról indulva a szemközti sarokba. Szabály, hogy az egyik járólapról a másikra csak akkor léphetünk, ha oldalaik érintkeznek, illetve séta közben mindig távolodnunk kell az első járólaptól. A kertész szeretné úgy elhelyezni a járólapokat, hogy a lehetséges séták száma éppen egy előre kitalált \(\displaystyle k\) érték legyen. Ugyanakkor szeretné az utak létrehozásához a legkevesebb járólapot vásárolni, de sajnos nem tudja meghatározni, hogy ez mennyi legyen. Készítsünk programot, amely megadja ezt a legkisebb értéket.
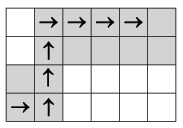
A program standard bemenete a telek \(\displaystyle a\) és \(\displaystyle b\) mérete, illetve a lehetséges séták \(\displaystyle k\) száma. A program adja meg a standard kimeneten a \(\displaystyle k\)-féleképp sétálható utak közül a legkevesebb járólappal rendelkező utakhoz szükséges járólapok számát, illetve \(\displaystyle -1\)-et, ha nem lehetséges \(\displaystyle k\)-féleképp bejárható úthálózatot készíteni. A mellékelt ábra a lenti példa egy lehetséges megoldását szemlélteti, illetve egy sétát mutat a nyilakkal.
| Bemenet | Kimenet |
| 4 6 10 | 13 |
Korlátok: \(\displaystyle 2 \le a, b \le 20\), \(\displaystyle 2 \le k \le 10^6\).
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb bemeneti értékek esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy s124.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
A beküldési határidő 2018. április 10-én LEJÁRT.
A beküldött megoldások helyeen, bár az időkorlátot meghaladó módon oldották meg a feladatot.
A megoldások a nagyobb bemeneteknél mért futásidő alapján kaptak több-kevesebb pontot.
Mintaként Ürmössy Dorottya, 9. osztályos budapesti diák munkáját adjuk közre: s124doku.txt, Program.cs.
Az alkalmazott tesztállományok és helyes kimenet: s124beki.zip.
Statisztika:
3 dolgozat érkezett. 10 pontot kapott: Ürmössy Dorottya. 8 pontot kapott: 1 versenyző. 6 pontot kapott: 1 versenyző.
A KöMaL 2018. márciusi informatika feladatai

