Az S. 127. feladat (2018. szeptember)

S. 127. Egy országban \(\displaystyle N\) darab város van, amiket kétirányú utak kötnek össze. Az úthálózatra teljesül, hogy bármelyik városból bármelyikbe el lehet jutni. Két város között legfeljebb egy közvetlen út van. Minden útra adott egy súlykorlátozás, hogy rakománnyal együtt legfeljebb mekkora tömegű teherautó mehet rajta. Egy áruszállító cég nyersanyagokat szállít városok között. A cégnek nem számít, hogy két város között a szállítás milyen hosszú úton történik, de a lehető legtöbb nyersanyagot szeretnék elvinni egy-egy teherautóval. Adott \(\displaystyle Q\) darab várospár, amik között nyersanyagot kell szállítani. Minden várospárra adjuk meg, hogy legfeljebb milyen nehéz lehet a teherautó szállítmánnyal.

Bemenet: az első sor tartalmazza a városok \(\displaystyle N\) számát, az utak \(\displaystyle M\) számát és a várospárok \(\displaystyle Q\) számát. A városokat 0-tól \(\displaystyle (N-1)\)-ig indexeljük. A következő \(\displaystyle M\) sor mindegyike három számot tartalmaz: egy adott út mely városokat köt össze, és mekkora rá a súlykorlátozás. A következő \(\displaystyle Q\) sor mindegyike két számot tartalmaz: egy adott várospár indexeit, amik között szállítani kell.

Kimenet: \(\displaystyle Q\) sor mindegyikébe egy számot írjunk: azt a maximális súlyt, amilyen nehéz teherautó indulhat az adott várospár között.

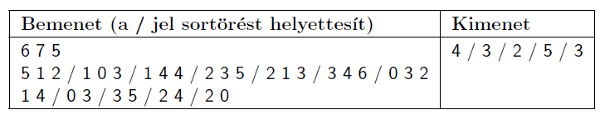
Korlátok: \(\displaystyle 2\le N, Q\le {10}^{5}\), \(\displaystyle N-1\le M\le 5\cdot {10}^{5}\), \(\displaystyle 1\le \text{súlykorlátok}\le {10}^{9}\), egész számok.

Értékelés: a pontok 20%-a kapható, ha egy útra a súlykorlát csak 1 vagy 2 lehet; további 20% kapható, ha \(\displaystyle N\le 100\); további 20% kapható, ha \(\displaystyle M\cdot Q\le {10}^{6}\); további 40% kapható az eredeti korlátokra.

Időlimit: 0,7 mp, memórialimit: 100 MiB.

Az I/S és S-jelű feladatok megoldását a http://mester.inf.elte.hu automatikus értékelő rendszer segítségével kipróbálhatod, tesztelheted (Téma: KöMaL - 2018/19).

(10 pont)

A beküldési határidő 2018. október 10-én LEJÁRT.

Statisztika:

13 dolgozat érkezett.
10 pontot kapott:	Csertán András, Molnár Bálint, Noszály Áron.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	2 versenyző.
6 pontot kapott:	2 versenyző.
5 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2018. szeptemberi informatika feladatai