Az S. 150. feladat (2021. február)

S. 150. Van egy \(\displaystyle N\times M\) mezőből álló játéktáblánk, melynek egyes mezői lyukasak. Van továbbá egy \(\displaystyle 1\times 1\times 2\) oldalú téglatestünk, melyet a következő szabályok szerint mozgathatunk a táblán: a téglatestnek minden lépés után teljes felületével szilárd mezőn kell állnia (különben leesik); a téglatestet minden lépésben egy hosszú vagy egy rövid, a talajon lévő élén átforgatva mozgathatjuk a szomszédos mezőkre.

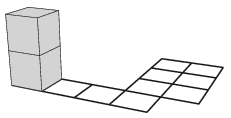
Arra vagyunk kíváncsiak, hogy el lehet-e juttatni a táblán elhelyezett téglatestet a kiinduló mezőjéről egy adott célmezőre. A téglatestnek a kiinduló és a célmezőjén is egy \(\displaystyle 1\times 1\)-es oldalán kell állnia.

Bemenet: az első sor tartalmazza a tábla sorainak és oszlopainak számát, azaz \(\displaystyle N\)-et és \(\displaystyle M\)-et. A következő \(\displaystyle N\) sor mindegyikében \(\displaystyle M\) karakter található. Az \(\displaystyle i\)-edik sor \(\displaystyle j\)-edik karaktere ,,#'', ha a mező nem lyukas, és ,,.'', ha a mező lyukas. A következő sorban a megválaszolandó kérdések \(\displaystyle Q\) száma szerepel. Az utána lévő \(\displaystyle Q\) sor mindegyikében egy téglatest kezdő mezőjének sor- és oszlopindexe, majd egy célmező sor- és oszlopindexe szerepel szóközzel elválasztva. A sorokat és oszlopokat nullától indexeljük.

Kimenet: az a szám, ahány kérdésre igen a válasz.

Példa:

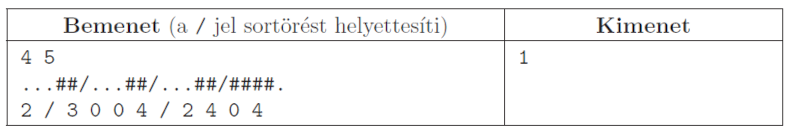
Magyarázat: az első téglatest az alábbi lépésekkel eljuthat a célba: elfektetés a \(\displaystyle (3,1)\) és \(\displaystyle (3,2)\) mezőkre, felállítás a \(\displaystyle (3,3)\)-ra, elfektetés az \(\displaystyle (1,3)\) és \(\displaystyle (2,3)\) mezőkre, átfordítás az \(\displaystyle (1,4)\)–\(\displaystyle (2,4)\)-re, felállítás a \(\displaystyle (0,4)\)-re. A második téglatest nem juttatható el a célba álló helyzetben.

Korlátok: \(\displaystyle 1\le N, M\le 200\), \(\displaystyle 1\le Q\le 10\,000\). Időkorlát: 0,5 mp.

Értékelés: A pontok 50%-a kapható, ha \(\displaystyle Q=1\).

Beküldendő egy s150.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2021. március 16-án LEJÁRT.

Azonosítsuk a játék állapotait (gráf csúcsait) a legkisebb koordinátájú mezővel , amit a téglatest lefed (bal felső), illetve a téglatest orientációjával. Ez felülről nézve lehet álló, vízszintesen fekvő vagy függőlegesen fekvő. Vegyük észre, hogy ha a egy \(\displaystyle A\) állapotból eljuthatunk egy \(\displaystyle B\) állapotba, akkor \(\displaystyle B\)-ből is eljuthatunk \(\displaystyle A\)-ba, azaz a gráf irányítatlan. Ennek az a következménye, hogy bármely két, egy komponensbe tartozó csúcs elérhető egymásból.

Így a kérdések megválaszolásához csak azt kell megmondanunk, egy komponensbe tartoznak-e. A komponenseket irányítatlan gráfnál mélységi bejárással meghatározhatjuk. A bejárás során minden csúcsot felcímkézünk a komponens sorszámával, majd a kérdések megválaszolásakor ezt \(\displaystyle O(1)\) alatt lekérdezzük.

Komplexitás: \(\displaystyle O(3*N*M)\) a bejárásokra és \(\displaystyle O(Q)\) a kérdésekre. Összesen: \(\displaystyle O(N*M+Q)\)

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Horcsin Bálint, Kovács Alex, Sándor Péter, Varga 256 Péter.
5 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. februári informatika feladatai