Az S. 158. feladat (2022. január)

S. 158. Egy négyzethálón adott egy sokszög, melynek oldalai a rácsvonalakra illeszkednek. Van \(\displaystyle D\) számú dobozunk. Egy-egy dobozban 1, 2 és 3 egység hosszú pálcikák vannak, melyek összhossza megegyezik a sokszög kerületével. Kérdés, hogy le lehet-e fedni a sokszög oldalait az egyes dobozokban található pálcikákkal azok eltörése nélkül? Több pálcika alkothat egy hosszabb oldalt. Készítsünk programot, amely a sokszög és minden egyes doboz esetén megválaszolja a kérdést!

Bemenet: az első sor tartalmazza a sokszög csúcsainak \(\displaystyle N\) számát. A következő \(\displaystyle N\) sor mindegyike egy-egy csúcs \(\displaystyle x\) és \(\displaystyle y\) koordinátáját tartalmazza a sokszög valamilyen irányú körüljárása szerint. A sokszög első és utolsó csúcsa is élet alkot. A következő sorban a dobozok \(\displaystyle D\) száma van. Ezután \(\displaystyle D\) sorban az egyes dobozok tartalmát írjuk le. Ezek mindegyike három szám, melyek rendre az 1, 2, illetve 3 hosszú pálcikák darabszáma a dobozban.

Kimenet: \(\displaystyle D\) sort kell kiírni. Ezek mindegyike ,,IGEN'', ha a sokszög oldalai a doboz tartalmával lefedhetők és ,,NEM'' különben.

Példa:

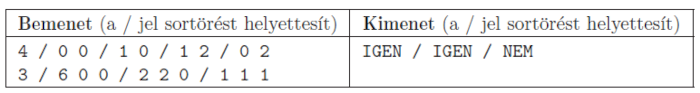
Korlátok: a koordináták abszolút értéke és a kerület is legfeljebb \(\displaystyle 10^5\). Időlimit: 1 mp.

Értékelés: a pontok 30%-a kapható, ha a program a legfeljebb 20 kerületű tesztesetekre helyes megoldást ad.

Beküldendő egy s158.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2022. február 18-án LEJÁRT.

Statisztika:

4 dolgozat érkezett.
10 pontot kapott:	Sándor Péter, Tóth 057 Bálint.
2 pontot kapott:	2 versenyző.

A KöMaL 2022. januári informatika feladatai