Az S. 165. feladat (2022. november)

S. 165. Egy gyorsétteremlánc két különböző étteremben dolgozó alkalmazottja rájött, hogy ha a jelenlegi munkahelyük helyett egymás munkahelyére járnának dolgozni, akkor mindkettőjüknek kevesebbet kellene utazni. Szeretnének javaslatot tenni a felettesüknek a munkahelyek újraosztására, de a probléma sajnos túl bonyolultnak bizonyult, hogy papíron kiszámolják.

Adott egy város úthálózata, mely csúcsokból és az őket összekötő súlyozott élekből áll. Van továbbá valahány éttermünk és \(\displaystyle D\) alkalmazottunk, akikről tudjuk, honnan és hova járnak dolgozni. A feladatunk úgy újraosztani a munkahelyeket, hogy az alkalmazottak munkahelytől vett távolságának összege a lehető legkisebb legyen. (Tegyük fel, hogy a dolgozóknak egyéb preferenciája nincs.)

A bemenet első sorában a csúcsok \(\displaystyle N\) és az élek \(\displaystyle M\) száma található. A következő \(\displaystyle M\) sor egy-egy utat ír le, a két végpontjának sorszámával és az él súlyával (az út hosszával). Ezután az alkalmazottak \(\displaystyle D\) száma, majd \(\displaystyle D\) sorban az alkalmazottak lakhelyének és munkahelyének csúcsszáma található. Mindent 0-tól indexelünk és egy csúcsban legfeljebb egy étterem van.

A kimenet egyetlen sorában az elérhető legkisebb távolságösszeg szerepeljen, ha az újraosztás után minden étteremben ugyanannyian dolgoznak, mint előtte.

Példa:

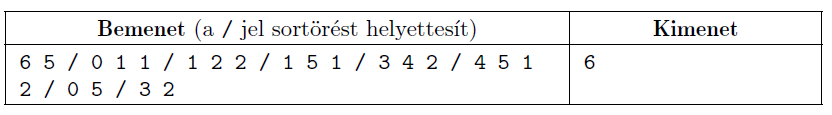
Megjegyzés: Mint ahogy a példa is mutatja, előfordulhat, hogy valaki így többet fog utazni.

Korlátok: \(\displaystyle N \le 500\), \(\displaystyle M \le 1000\), \(\displaystyle D \le 100\). Időlimit: 1 mp.

Értékelés: A pontok 50%-a kapható, ha a program helyes kimenetet ad a \(\displaystyle {D \le 10}\) esetekre.

Beküldendő egy s165.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

A beküldési határidő 2022. december 15-én LEJÁRT.

Statisztika:

2 dolgozat érkezett.
5 pontot kapott:	2 versenyző.

A KöMaL 2022. novemberi informatika feladatai