Az S. 167. feladat (2023. január)

S. 167. Egy hegy tetejére \(\displaystyle N\) lépcsőből álló lépcsősor vezet fel. Egy szerzetes \(\displaystyle T\) egymást követő napon felment a hegyre. Első nap az \(\displaystyle l_{1}\) lépcsőfokról indult és minden lépésnél kihagyott \(\displaystyle d_{1}\) lépcsőfokot. Rálépett tehát az \(\displaystyle l_{1}+(d_{1}+1)\), \(\displaystyle l_{1}+ {2(d_{1}+1)}\), \(\displaystyle \ldots\ \) lépcsőfokokra egészen addig, míg fel nem ért a hegycsúcsra. Ha az utolsó lépés magasabbra ért volna, mint \(\displaystyle N\), akkor rálépett az \(\displaystyle N\)-edik fokra és ezzel feljutott a hegycsúcsra.

Az első napot követő napokon az \(\displaystyle l_{i}\) és \(\displaystyle d_{i}\) értékeket a következő szabály szerint változtatta: \(\displaystyle l_{i+1} = (l_{i}+1) \mod L\) és \(\displaystyle d_{i+1} = (d_{i}+1) \mod D\), ahol \(\displaystyle 1\le i\le T-1\). Sajnos a szerzetes már nem emlékszik rá, hogy így hány lépcsőfokra lépett rá felfelé menet. Készítsünk programot, ami meghatározza ezt a számot.

A bemenet első sorában hat egész szám szerepel: a lépcsők \(\displaystyle N\) száma, a napok \(\displaystyle T\) száma, az \(\displaystyle L\) és \(\displaystyle D\) modulusok, illetve az első napon az \(\displaystyle l_{1}\) lépcsőfok, amiről indulunk, és a lépésenként kihagyott lépcsőfokok \(\displaystyle d_{1}\) száma.

A kimenet első és egyetlen sorába írjuk ki, hogy összesen hány lépcsőfokra lépett rá a szerzetes felfelé menet.

Példa:

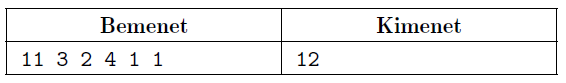
Magyarázat: az első napon az első fokról indul és minden másodikra lép rá (5 lépés). A második napon a nulladik fokról indul és minden harmadik lépcsőfokra lép rá (4 lépés). A harmadik napon az első fokról indul és minden negyedikre lép rá (3 lépés).

Korlátok: \(\displaystyle 1\le N,T \le 10^9\), \(\displaystyle 1\le L,D \le 400\), \(\displaystyle L,D\le N\), \(\displaystyle 0\le l_{1}< L\), \(\displaystyle 0\le d_1< D\). Időkorlát: 1 mp.

Értékelés: A pontok 40%-a kapható, ha a program helyes kimenetet ad a \(\displaystyle {T\le 10^5}\) bemenetekre.

Beküldendő egy s167.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

A beküldési határidő 2023. február 15-én LEJÁRT.

Statisztika:

2 dolgozat érkezett.
10 pontot kapott:	Szabó Imre Bence.
3 pontot kapott:	1 versenyző.

A KöMaL 2023. januári informatika feladatai