Az S. 34. feladat (2008. március)

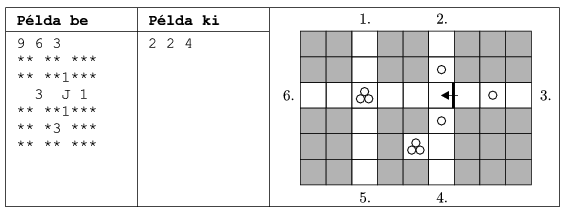
S. 34. Bergengócia királya elérkezettnek látja az időt, hogy férjhez adja leányát, ezért legjobb építészével egy sárkányokkal teli labirintust terveztet. A királylány kezét csak az a lovag nyerheti el, aki ennek egyik bejáratán belépve sikeresen kijut bármelyik másik bejáraton. A király parancsa szerint olyan labirintust kell tervezni, hogy a lovag bármelyik kijáratot is választja, útközben legalább bizonyos számú sárkányfejet le kell vágnia.

Ilyen fontos döntés esetén a király még leghűségesebb embereiben sem bízhat. Így minket kért meg, hogy írjunk programot, mely ellenőrzi, hogy az építész által elkészített labirintusterv teljesíti-e a kívánalmakat.

A program az alaprajzot fájlból olvassa, az eredményt fájlba írja. A bemeneti, illetve kimeneti fájlok nevei az első, illetve második parancssori argumentumok.

A bemenet első sorában szóközzel elválasztva W, H és F, a labirintus szélessége, magassága és a levágandó sárkányfejek minimális F száma szerepel (3 $\le$ W,H $\le$ 100). Az ezt követő H sor mindegyike W karaktert tartalmaz, mely:

szóköz, ha az adott mező folyosó, melyről tetszőleges szomszédos folyosóra lehet lépni

J, B, F és L, ha az adott mező folyosó, és egy olyan kapu van rajta, melynek hatására a mezőről jobbra, balra, fel vagy lefelé nem lehet lépni

*, ha a mező fal

N=1-9 számjegy, ha a mező folyosó és rajta egy N-fejű sárkány rejtőzik, melyet a mezőre lépve mindenképp le kell győzni.

Bejáratnak a labirintus szélén lévő folyosókat tekintjük, amelyekről feltehetjük, hogy mindig üresek lesznek, illetve legalább 1 fal határolja őket.

A kimenet egyetlen sora $K\ A\ B$ alakban három, szóközzel elválasztott számot tartalmazzon: ha a terv helyes, mindhárom érték legyen 0, egyébként egy olyan A bejárattól B kijáratig vezető útvonal leírása, mely során csak K (K<F) sárkányfejet kell levágnunk. A bejáratokat a bal felső saroktól kezdődően az óramutató járásával megegyezően, 1-től kezdve számozzuk, több megoldás esetén a legkisebb K, majd ezen belül a legkisebb A, majd B értékűt írjuk ki.

Beküldendő a program forráskódja (s34.pas, s34.cpp, ...), valamint a program rövid dokumentációja (s34.txt, s34.pdf, ...), amely tartalmazza a megoldás vázlatos leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2008. április 15-én LEJÁRT.

Első lépes

Egy programozási/algoritmizálási feladat megoldásának első lépése mindig az absztrakció: azért, hogy a megoldás során valóban a feladatra tudjunk koncentrálni, célszerű a feladat szövegében megjelenő érdektelen részletektől elvonatkoztatni, csak a lényeget kiemelni. Esetünkben a probléma érdemi részét remekül lefordíthatjuk a gráfok nyelvére. A labirintushoz rendeljünk hozzá egy $G=\left(V,E\right)$ súlyozott irányított gráfot a következő módon: a gráf V csúcsai az egyes mezőknek feleljenek meg, élek pedig a szomszédos mezőknek megfelelő csúcsok között fussanak. Az a $\in$ V-ból b $\in$ V csúcsba futó e $\in$ E él $c\left(e\right)$ súlya a-ból b-be jutáshoz levágandó sárkányfejek számát jelölje, azaz a következő legyen: ha b fal, vagy a-ról nem lehet rálépni (kapu miatt), akkor a súly legyen végtelen, egyébként pedig egyezzen meg a b mezőn lévő sárkányfejek számával (ez lehet zérus is). Ezen kívül jelölje d(v,w) a v és w csúcsok közti legrövidebb út hosszát, illetve i(w) egy w bejárati csúcs sorszámát.

Az így kapott gráfban egy A-adik bejárattól B-edikig vezető, K sárkányfej levágását igénylő útvonal a gráfban egy K költségű, a megfelelő csúcsok között futó útnak felel meg. A feladatot pedig a következőképpen fogalmazhatjuk meg: adjuk meg a gráfban a legrövidebb, bejárati csúcsok között vezető x $\rightarrow$ y irányított utat. A megadás az út végpontjainak $A=i\left(x\right)$ , $B=i\left(y\right)$ sorszámával, illetve az út $K=d\left(x,y\right)$ hosszával történjen. Több legrövidebb út esetén a legkisebb A, majd B értékűt adjuk meg, ezt a továbbiakban az optimális megoldásnak fogjuk nevezni.

A továbbiakban fontos lesz fejben tartani, hogy az optimális megoldás megadásához lényegében nem mást teszünk, mint az összes bejáratok között futó összes utakat leíró összes $\left(K',A',B'\right)$ számhármasok halmazából kiválasztjuk a legjobbat, azaz a legkisebb K', majd A', majd B' értékűt. A hangsúly azon van, hogy e exponenciális méretű halmaz elemeiből minél kevesebbet kelljen egyáltalán számba vennünk, az optimum kiválasztásához.

Első megközelítés

Kézenfekvő ötlet, hogy minden bejáratból indítunk egy legrövidebbút-keresést az összes többi pontba - például Dijkstra algoritmusával. Ugyanakkor ezzel rengeteg felesleges munkát végzünk: csupán azt szeretnénk tudni ugyanis, hogy F-nél rövidebb út létezik-e egyáltalán egy bejáratból egy másikba, az számunkra teljességgel érdektelen, hogy mindenféle bejáratokból mindenféle pontokba mekkora a legrövidebb utak hossza. Dijkstra algoritmusának futásideje $O\left(\left(n+e\right)logn\right)$ , ahol n a gráf csúcsainak, e pedig éleinek a száma, mely utóbbi esetünkben a négyzetháló-topológia miatt n-nel arányos. Mivel az algoritmust minden bejáratra lefuttatjuk, melyből (a oldalhosszú négyzetalakú labirintust feltételezve) $O\left(a\right)$ van, az így kapott algoritmus műveletigénye $O\left(a\left(a^{2}+a^{2}\right)loga^{2}\right)=O\left(a^{3}loga\right)$ .

Hasonló módon rengeteg felesleges munkát végeznénk, ha például Warshall algoritmusával meghatároznánk minden pontpárok között a legrövidebb utak hosszát.

Egy hatékony megoldás irányítatlan gráfokra

Az egyszerűség kedvéért oldjuk meg először az előbbi irányítottgráf-modellre felírt problémát egy irányítatlan gráfra, majd ezután terjesszük ki az algoritmust az irányított esetre! Fontos megjegyezni, hogy az irányítatlan gráf már nem modellezi az eredeti feladatot, hiszen például a kapukat sehogyan sem tudjuk reprezentálni. A tárgyalás érdekében azonban mindenképp érdemes bevezetni ezt a további - ha úgy tetszik - veszteséges absztrakciót.

Alkalmazzuk az első bekezdésben bevezett jelöléseket! Bejáratoknak továbbra is a gráf csúcsainak egy adott részhalmazát tekintsük, illetve ahogyan már tárgyaltuk, több megoldás esetén pedig az optimálisnak pedig azt az, melynél az A $\neq$ B értékek a lehető legkisebbek. A két végpont sorrendje most viszont az irányítatlanság miatt érdektelen. Vezessük még be a következőket: jelölje $b\left(v\right)$ a v csúcshoz legközeleb eső bejárati csúcsot (több, azonos távolságra lévő bejárat esetén a legkisebb sorszámút), $\dot{d}\left(v\right)=d\left(v,b\left(v\right)\right)$ pedig v ettől vett távolságát. A w bejárati csúcsokra legyen definíció szerint $b\left(w\right)=w$ .

Tegyük fel, hogy valamilyen módon a b és $\dot{d}$ értékeket már minden csúcsra kiszámoltuk (a d értékeket csak a bizonyításhoz használjuk, a megoldás kiszámításához nem szükségesek). Tegyük fel, hogy az optimális megoldás az $A=i\left(x\right)$ sorszámú x bejárati csúcsból a $B=i\left(y\right)$ sorszámú y-ba érkezik, és $K=d\left(x,y\right)$ költségű!

Lemma 1. Az optimális út minden v csúcsára $b\left(v\right)=x$ vagy $b\left(v\right)=y$ .

Biz. A végpontokra az állítás bejárati csúcs voltuk miatt áll. Egy közbülső v pontra tegyük fel, hogy $b\left(v\right)=z\neq x,y$ . Ez vagy akkor áll fenn, ha $d(v,z)<min\left\{ d(v,x),d(v,y)\right\}$ vagy pedig ha $d(v,z)=min\left\{ d(v,x),d(v,y)\right\}$ de az $i\left(z\right)$ sorszáma kisebb. Ekkor x,y közül bármelyik bejáratot lecserélve z-re az első esetben egy rövidebb, a második esetben pedig egy alacsonyabb bejárati sorszámú, tehát mindkét esetben egy jobb utat kapnánk, ami ellentmond annak a feltételnek, hogy az eredeti út optimális.

Lemma 2. Az optimális útnak van olyan $\left\{ v,w\right\}$ éle, hogy b(v)=x és b(w)=y. Ezekre az élekre $c\left(v,w\right)+d(v,x)+d(w,y)=d\left(x,y\right)$ .

Biz. Mivel az út csúcsainak b-értéke az 1. lemma miatt csak x vagy y lehet, és a végpontok b-értékei különböznek, biztosan van egy ilyen él. A második állítás pedig azért igaz, mivel a bal oldalon is az x-y út hossza szerepel, csak három szakaszra (x-v,v-w,w-y) egyenként összegezve.

A 2. lemma állítását felhasználva azonnal konstruálhatunk is egy algoritmust a feladat megoldására. Vegyük ugyanis sorra a gráf éleit, és minden $\left\{ v,w\right\}$ élre képezzük az adott élen áthaladó utat leíró $\left(K',A',B'\right)$ számhármast a következő módon:

$A'=i\left(b\left(v\right)\right)$

$B'=i\left(b\left(w\right)\right)$

$K'=c\left(v,w\right)+\dot{d}(v)+\dot{d}(w)$

Az így képzett legális (A' $\neq$ B') számhármasokat mint potenciális megoldásokat jegyezzük meg, majd közülük válasszuk ki a legjobbat, azaz a legkiseb K', majd A', majd B' értékűt. Az így kapott számhármas épp az optimális megoldást írja, hiszen a 2. lemma miatt a gráf tartalmazott legalább 1 olyan $\left\{ v,w\right\}$ élet, melyre:

b(v)=x, így $A'=i\left(b\left(v\right)\right)=i\left(x\right)$

b(w)=y, így $B'=i\left(b\left(w\right)\right)=i\left(y\right)$

$c\left(v,w\right)+d(v,x)+d(w,y)=d\left(x,y\right)$ , így $K'=c\left(v,w\right)+\dot{d}(v)+\dot{d}(w)=c\left(v,w\right)+d(v,x)+d(w,y)=d\left(x,y\right)$

Azaz az ebből az élből képzett $\left(K',A',B'\right)$ hármas épp az optimális megoldást leíró $\left(K=d\left(x,y\right),A=i\left(x\right),B=i\left(y\right)\right)$ hármassal egyezik meg, azaz a potenciális megoldások között az optimális megoldás is szerepelt, így amikor közülük a legjobbat kiválasztottuk, az épp az optimális megoldás volt.

Már csak a b-értékek, illetve az egyes pontok legközelebbi bejárattól vett $\dot{d}\left(v\right)=d\left(v,b\left(v\right)\right)$ távolságértékeinek a meghatározása maradt hátra. A bejárati csúcsokra $\dot{d}\left(w\right)=0$ és $b\left(w\right)=w$ . Ezután pedig Dijkstra algoritmusának egyszeri lefuttatásával megkaphatjuk a két értéket az összes többi pontra (a legrövidebbút-keresést az összes bejárati csúcsból egyszerre indítva, a b-értékeket a minimumot adó őstől másolva).

A megoldás kiterjesztése irányított gráfokra

Irányított élek esetén mindössze annyi változik, hogy mind a $\dot{d}$ , mind pedig a b értékekből két készletünk van: az egyik arra vonatkozik, amikor az élek irányításának megfelelően haladunk ( $b_{e},\dot{d}_{e}$ ), a másik pedig az irányítással ellentétes haladásra ( $b_{v},\dot{d}_{v}$ ). Kiszámításuk külön-külön, az előző bekezdésben leírt módon történik, tehát összesen 2 db legrövidebút-keresésre van szükségünk. Az éleket sorban megnézve a $\left(v,w\right)$ irányított él a következő potenciális megoldást adja:

$A'=i\left(b_{v}\left(v\right)\right)$

$B'=i\left(b_{e}\left(w\right)\right)$

$K'=c\left(v,w\right)+\dot{d}_{v}(v)+\dot{d}_{e}(w)=c\left(v,w\right)+d_{v}(v,x)+d_{e}(w,y)$

Az optimális megoldást itt is a potenciális megoldásokat leíró számhármasok közül a legjobbat választva kapjuk.

A algoritmus műveletigénye általános esetben $O\left(e+\left(n+e\right)logn\right)$ , mivel konstans számú (2 db) legrövidebbút-keresést hajtunk végre, illetve egyszer végiglépkedünk az összes élen. Esetünkben a gráf kötött felépítése miatt a műveletigény $O\left(a^{2}+\left(a^{2}+a^{2}\right)loga^{2}\right)=O\left(a^{2}loga\right)$ , ami felhasználva, hogy az élsúlyok egy kis elemszámú halmazból származnak (0...9, ha végtelen súly esetén az élet kitöröljük) Dijkstra algoritmusának mozgókupacos megvalósításával $O\left(a^{2}\right)$ -re csökkenthető, azaz a feladat meglepő módon a mezők számával egyenesen arányos időben megoldható.

Engedy Balázs

Statisztika:

5 dolgozat érkezett.

7 pontot kapott: 2 versenyző.

5 pontot kapott: 1 versenyző.

4 pontot kapott: 1 versenyző.

2 pontot kapott: 1 versenyző.

A KöMaL 2008. márciusi informatika feladatai

5 dolgozat érkezett.
7 pontot kapott:	2 versenyző.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?