 |
Az S. 42. feladat (2009. február) |
S. 42. Írjunk programot, mely képes a ,,Tetris'' játék következő változatával játszani.
A játéktér egy egységnyi oldalhosszúságú cellákból felépített négyzetrács, melyet oldalról és alulról falak határolnak, felülről azonban nyitott. A játékos a végtelen magasságból véletlenszerűen, egyesével érkező, különféle alakú, egységnégyzetekből összeállított alakzatok egymásra helyezésével egy tornyot épít. Célja, hogy az alakzatokat úgy helyezze el, hogy az idő múlásával - az elemek érkezésével - a torony magassága a lehető legkisebb legyen.
Egy alakzat akkor számít szabályosan elhelyezettnek, ha egyetlen másik alakzatba sem lóg bele, az őt alkotó egységnégyzetek közül viszont legalább egy alulról érintkezik egy korábban elhelyezett alakzattal vagy az alsó fallal, valamint az alakzat elhelyezése megvalósítható egy végtelen magasságban végzett elforgatás és vízszintes eltolás, majd egy függőleges leeresztés egymásutánjaként anélkül, hogy e művelet közben az alakzat bármely más alakzattal átfedésbe kerülne.
A lehetséges hatféle alakzatot az ábécé kisbetűivel azonosítjuk:

A program futása során a standard be- és kimenetén keresztül, újsorral elválasztott szöveges üzenetek formájában interaktívan kommunikál egy főalkalmazással, mely az alakzatok sorsolását és a lépések ellenőrzését végzi. A főalkalmazás különféle események bekövetkezéséről a játékos programját a standard bemenetre küldött egy-egy üzenet formájában értesíti. Ezek szintaxisa:
start <W>
o Egyetlen egyszer, a futtatás legelején érkezik, a játéktér 3 W
W 32 szélességét adja meg. Erre a játékosnak nem kell válaszolnia.
32 szélességét adja meg. Erre a játékosnak nem kell válaszolnia.
item [ojlszi]
o Egy új elem érkezését jelzi. Paramétere a felsoroltak közül egyetlen karakter. A várt válasz egy pos üzenet.
A játékos programja egyetlen típusú üzenetet írhat a standard kimenetre, ennek szintaxisa:
pos <bal oldal pozíciója az elforgatás után> <OJE elforgatás, fok>
o Az item üzenetre várt válasz az új elem kívánt elhelyezését írja le: az elforgatás után melyik oszlopban legyen a bal széle (1 és W-s+1 közötti egész, ahol s az alakzat szélessége az elforgatás után), és mennyivel forgassuk el az elemet (értéke 0, 90, 180 vagy 270, az óramutató járásával ellentétesen, fokban).
A program a következő elemet leíró üzenetet a standard bemenetére csak azután kapja, hogy az előző elem elhelyezését leíró választ a standard kimenetre kiírta. Figyeljünk arra, hogy valóban a standard be- és kimenetet használjuk, ne a billentyűzetet és/vagy a képernyőt. Az üzenetek végén ne feledjük az újsort, a kimeneti puffert mindig ürítsük az adott válasz kiírása után. Pascal esetén ne használjuk a "Crt" modult, C/C++ esetén a conio.h állományt.
Példaképp tekintsük a mellékelt párbeszédet (dőlttel szedtük a program válaszait).
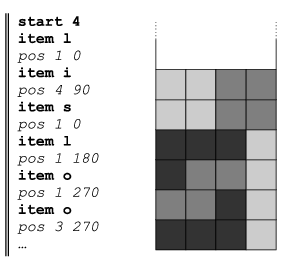
(10 pont)
A beküldési határidő 2009. március 16-án LEJÁRT.
A megoldás menete
Nyilvánvaló, hogy mivel az n-edik elemet az előtt kell elhelyeznünk, hogy bármiféle információval rendelkeznénk az n+1-edik és további elemekről, illetve a játék akármelyik pillanatban abbamaradhat, a problémára tökéletes megoldás nem adható. A feladat egy minél jobb közelítő (heurisztikus) megoldás elkészítése volt, két szempontból is: egyrészt egy olyan megoldást kellett adni, mely olyan tornyot épített, melynek magasságát bármikor mintavételezve átlagosan minél kisebb értéket kapunk (tehát nem feltétlen minden pillanatban optimális, de mindig közel van az optimumhoz), másrészt a gyorsaság érdekében az elemek elhelyezését célszerű volt valamilyen jóságfüggvény alapján végezni, ahelyett, hogy fabejárással a döntés lehetséges következményeit vizsgálnánk az összes lehetséges következő N elem esetén.
Egy új elem adott elhelyezésének értékelése során két szempontot volt célszerű figyelembe venni: egyrészt azt, hogy a torony magassága a lehető legkisebb mértékben növekedjen, másrészt pedig, hogy a lehető legkevesebb "lyuk" (azaz elem alatti üres hely) keletkezzen. Önmagában egyik módszer sem vezetett túl jó eredményre: amennyiben valaki csak a magasság rövid távú minimalizálására törekedett, úgy általában túl sok lyukat hozott létre, mely a magasságot hosszú távon jelentősen hátrányosan befolyásolta. Ha a lyukak minimalizálása volt az elsődleges (és azonos lyukszám esetén nyilvánvalóan jobbnak kell választani a kisebb magasságút), az - szerencsétlen elemsorozat esetén - általában ahhoz vezetett, hogy a torony tetején nyúlványok kezdtek el képződni: pl. ha nem jött olyan elem, amivel a torony közepét és széleit lehetett volna lyukmentesen lefedni, akkor gyakran a torony egyharmadánál és kétharmadánál kisebb tornyok kezdtek el épülni. Szerencsés esetben egy idő után a megfelelő elemek érkezésével ezek a völgyek feltöltődtek, de nem ritkán előfordult az is, hogy a megoldás kényszerhelyzetbe került, és nem tudott mást tenni, mint úgy elhelyezni egy elemet, hogy az rálógott egy ilyen völgy nyílására: katasztrofális következmény.
A legjobb heurisztika úgy adódik, hogy amennyiben nem okoz (a torony felszínén) túl nagy magasságkülönbséget a lyukmentes elhelyezés, azt választjuk, egyébként pedig feláldozunk néhány lyukat a nyúlványok elkerülése érdekében. További (megfelelő elemhalmaz esetén minimális) javulás érhető el, ha az elemek elhelyezésekor figyelünk arra, hogy a fenti megfontolásokon túl úgy helyezzük azokat el, hogy a későbbiekben minél jobban tudjunk rájuk építkezni.
Ezek után már csak ki kellett értékelni a lehetséges elhelyezéseket, és a legjobb elhelyezést kiválasztani. Ez legfeljebb W-vel arányos lépés, ha pályáról csak azt tároljuk, hogy az adott oszlopban milyen magasan helyezkedik el a legfelső elem -- vegyük észre, hogy ennyi elegendő is.
A beérkezett megoldások értékelése
A feladatra sok kiváló megoldás érkezett, melyeknek nagyon örültünk.
A pontozás a következőképpen alakult: a programra, attól függően, hogy a megoldás mennyire volt optimális, legfeljebb 8 pontot lehetett kapni, a megfelelő dokumentáció és az olvasható, jól kommentezett kód 2 pontot ért. A működőképes (és az azzá tett) megoldások között versenyt szerveztünk, mely során I., II. és III. díjat osztottunk ki. Az első díjért legfeljebb 8, másodikért 7, a harmadik díjért pedig legfeljebb 6 pontot lehetett kapni, a nem díjazott megoldások a "program" részre legfeljebb 5 pontot kaphattak. Amennyiben a program versenyképes állapotba juttatásához azon javítás(oka)t kellett végezni, az elért eredményre kapott pontszámot a hibá(k) súlyosságának megfelelően csökkentettük. Szeretnénk hangsúlyozni, hogy az igazságos pontozás érdekében a programokban kizárólag olyan hibákat javítottunk, melyek hatására a program belső pályareprezentációja sérült, vagy a javítókörnyezet számára küldött "pos" üzenetet nem azt az elemelhelyezést írta le, melyre a program gondolt: ezek a hibák ugyanis inkonzisztenciát eredményeztek a pálya tényleges állapota, illetve a között az állapot között, amelyben az adott program a pályát elképzelte, és hosszú távon teljesen rossz elemelhelyzésekhez vezettek (hiszen a program és a javítókörnyezet nem ugyanazon a pályán dolgozott). Ezek pedig értékelhetetlen eredményekhez vezettek, de legalább ugyanebből az okból kifolyólag ezen hibák jól detektálhatóak is voltak, így ezeket nagy biztonsággal javítani tudtuk. Az elemek szuboptimális elhelyezését eredményező implementációs hibák javítására viszont nem vállalkoztunk, ugyanis ezek egyrészt rendkívül nehezen azonosíthatóak, másrészt nehezen eldönthető, hogy egy adott programsor implementációs vagy elvi hibát tartalmaz, harmadrészt pedig egy sor javításával a megoldás teljesítménye (jósága) lényegesen megváltozhat, melynek következtében szinte lehetetlen lett volna ezen javításokat is figyelembe vevő, igazságos pontrendszert kidolgozni.
A versenyzők megoldásainak egy-egy 4, 8, 12, 16, 20, 24, 28, ill. 32 széles pályán kellett rendre 1000 elemet elhelyezni. A javítókörnyezet végezte az elemek sorsolását, elhelyezéseinek ellenőrzését, a lépések aktualizálását, majd rögzítését, illetve statisztikát is vezetett. A 17 beérkezett megoldás közül 13 vett részt az egymás elleni küzdelemben. Az egyes megoldások által épített tornyok magassága a különféle szélességű pályákon az 1000. elem elhelyezése után rendre a következő: (a -1 azt jelenti, hogy a program szabálytalan lépést tett)

A különböző méretű pályákon az egyes megoldásokat rangsoroltuk: a legjobb megoldások 1 pontot, a közepesen teljesítők 2-t, a gyengébben teljesítők 3-at, az illegális lépést végrehajtók 4 pontot kaptak. Az így kapott pontokat minden megoldásra összegeztük, és az így kapott pontszámokból alakítottuk ki a fenti rangsort. (A legkisebb 3 és a legnagyobb pálya csak félpontot ért.)
Részletes statisztikák
Az egyes pályákon a versenyzők által épített tornyok magasságának és az optimális torony magasságának a különbsége (aka.: extra magasság) a lépésszám függvényében:
A részletes teszteredmények, az építményekről készült képekkel innen letölthetőek (vigyázat, 10MB!).
Gyakori hibák
A legtöbb versenyzőnél előfordult, hogy a kimenetre írás után a kimeneti puffert nem ürítették (flush vagy annak megfelelő utasítással), melynek hatására a válasz "elakadt" a standard kimeneti csővezeték pufferében, így azt a javítókörnyezet nem tudta kiolvasni.
Néhány versenyzőnek a feladat pontos értelmezésével akadt problémája, ilyen esetekben bátran kérdezzetek a fórumon!
Mintamegoldás
Mintamegoldásként közöljük:
- Fábián András, 12. osztály, Szeged, Radnóti Miklós Kísérleti Gimnázium (Pascal, fabian.zip)
- Kovágó Zoltán, 9. osztály, Budapest, Szent István Gimnázium (C++, kovago.zip)
- Várnai Péter, 10. osztály, Budapest, ELTE Apáczai Csere János Gyakorló Gimnázium (FreeBASIC, varnai.zip)
versenyzők munkáját.
Statisztika:
17 dolgozat érkezett. 10 pontot kapott: Fábián András, Kővágó Zoltán, Várnai Péter. 9 pontot kapott: Englert Péter, Weisz Ágoston. 8 pontot kapott: 4 versenyző. 7 pontot kapott: 3 versenyző. 6 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2009. februári informatika feladatai
|
|








