 |
Az S. 46. feladat (2009. szeptember) |
S. 46. A legtöbb hiedelemvilággal ellentétben a bergengóc mitológiát mélyen áthatják a természettudományok világából származó elemek. Úgy tartják például, hogy balszerencsét hoz, ha egy hajó fővitorlája nem négyzet alakú, vagy oldalhossza -- méterben kifejezve -- nem kettőhatvány.
Ennek megfelelően a kikötőkben is kizárólag négyzet alakú, kettőhatvány oldalhosszú vitorlavásznakat kínálnak, illetve a varrodákban is csak négy egyforma méretű vászonból készítenek egy kétszer akkorát.
Készítsünk programot, mely a kikötőben kapható, különböző méretű vásznak árainak ismeretében meghatározza, hogy legolcsóbban mennyiért tehetünk szert egy kívánt méretű vitorlára.
A standard bemenet első sorában három, szóközzel ellátott egész szám: az eladásra kínált vitorladarabok száma, a készíteni kívánt vitorla 1
A=2a2048 oldalhossza, illetve a varratás folyóméterenkénti 0V1000 költsége szerepel. Azt ezt követő N darab sor mindegyike két egész számot, egy-egy portéka 1Bi=2biA oldalhosszát és árát tartalmazza. A sorok oldalhossz, majd ár szerint monoton növekvően rendezettek.
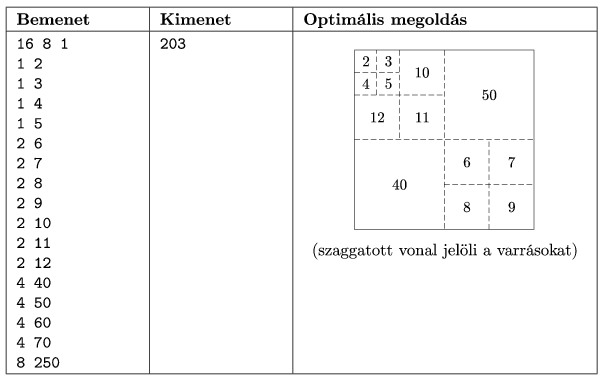
A standard kimenet egyetlen sorába egyetlen egész szám kerüljön: az a minimális összeg, amelyből elkészíthető a kívánt vitorla. (A teljes költség az alapanyag és az esetleges varratási díj összege.) Feltehetjük, hogy mindig van megoldás.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az s46.exe és más, a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét bemutató dokumentáció egy tömörített mappában (s46.zip).
A kiadott mintabemenetek: s46teszt.zip. Ezek közül legalább ötre kell rendben lefutnia és formailag helyes eredményt adnia a programnak. Részletesebb információ a Versenykiírásban, ill. a tömörített csomagban.
(10 pont)
A beküldési határidő 2009. október 12-én LEJÁRT.
Statisztika:
27 dolgozat érkezett. 10 pontot kapott: Berecz Dénes, Éles András, Mokcsay 026 Ádám, Várnai Péter. 9 pontot kapott: Adrián Patrik, Bodosi Eszter, Fejér 267 László, Kovács 125 András, Nagy 111 Miklós, Nagy Róbert. 8 pontot kapott: 8 versenyző. 7 pontot kapott: 4 versenyző. 6 pontot kapott: 2 versenyző. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző.
A KöMaL 2009. szeptemberi informatika feladatai