 |
Az S. 88. feladat (2014. március) |
S. 88. Adott egy irányítatlan gráf \(\displaystyle N\) (\(\displaystyle 1 \le N \le 100\;000\)) csúccsal és \(\displaystyle M\) (\(\displaystyle 1 \le M< N\)) éllel. Számítsuk ki, hogy hányféleképpen lehet az éleket úgy irányítani, hogy minden csúcsból legfeljebb egy él induljon ki. Adjuk meg ennek a számnak az 1000000007-tel vett osztási maradékát.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle M\)-et, majd a következő \(\displaystyle M\) sorból az \(\displaystyle a_i\), \(\displaystyle b_i\) (\(\displaystyle 1 \le a_i, b_i \le N\)) szóközzel elválasztott egészeket, melyek mindegyike egy-egy irányítatlan él két végpontját jelöli. Mivel a gráf nem feltétlenül egyszerű, ezért ugyanaz a számpár többször is szerepelhet a bemenetben. Írjuk a standard output első és egyetlen sorába a lehetőségek számát modulo 1000000007.
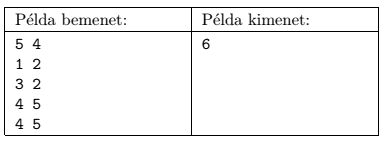
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Részpontszámok a következőkre kaphatóak:
\(\displaystyle \bullet\) a program \(\displaystyle N\le 200\)-ra megoldást ad;
\(\displaystyle \bullet\) a program \(\displaystyle N\le 5000\)-re megoldást ad.
Beküldendő egy tömörített s88.zip állományban a program forráskódja (s88.pas, s88.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s88.txt, s88.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2014. április 10-én LEJÁRT.
Mintamegoldásnak Makk László megoldását tesszük közzé. Oda kellett figyelni arra, hogy a gráfban lehetnek hurokélek is! s88.zip
Statisztika:
12 dolgozat érkezett. 10 pontot kapott: Makk László, Somogyvári Kristóf, Weisz Ambrus, Zalavári Márton. 9 pontot kapott: Alexy Marcell. 8 pontot kapott: 1 versenyző. 6 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2014. márciusi informatika feladatai