Az S. 94. feladat (2014. december)

S. 94. Egy állatkísérlet során a kutatók arra lettek figyelmesek, hogy ha túl sok állat léphet egymással kapcsolatba, akkor pontatlan lesz a kísérlet. Jelenleg egy \(\displaystyle N\times N\)-es négyzet alakú mezőn (\(\displaystyle 2\le N\le 17\)) túl sok állat tartózkodik. Szeretnénk \(\displaystyle K\) darab (\(\displaystyle 1\le K\le 2N-2\)) kerítést építeni nekik, hogy el legyenek különítve. Egy kerítés párhuzamos a mező valamelyik szélével, és attól egész távolságra halad. Továbbá a teljes négyzeten keresztül kell haladnia (azaz nem lehet vége egy kerítésnek a négyzet belsejében). Ilyen feltételek mellett szeretnénk minimalizálni az összefüggő részeken lévő állatok maximális számát.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle K\)-t (\(\displaystyle 2\le N\le 17\), \(\displaystyle 1\le K\le 2N-2\)), majd a következő \(\displaystyle N\) sorból soronként \(\displaystyle N\) egész számot, melyek jelentése: az adott sorban az adott egységnégyzetben ennyi állat tartózkodik. Írjuk a standard output első és egyetlen sorába a lehető legjobb kerítésépítés mellett a legtöbb állat számát, melyek egymástól nincsenek elkerítve.

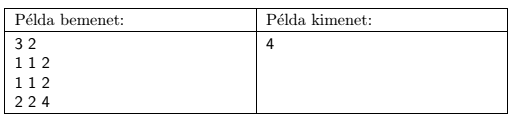
Magyarázat: Két kerítést kell építenünk, méghozzá a 2. és 3. oszlop, és a 2. és 3. sor között érdemes. Ekkor a bal felső részben \(\displaystyle 1+1+1+1=4\) állat lesz, a jobb felsőben \(\displaystyle 2+2=4\), a bal alsóban is \(\displaystyle 2+2=4\), és a jobb alsóban is 4 állat lesz, így 4-et írunk ki.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Beküldendő egy tömörített s94.zip állományban a program forráskódja (s94.pas, s94.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s94.txt, s94.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Gáspár Attila.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.

A KöMaL 2014. decemberi informatika feladatai