Az S. 96. feladat (2015. február)

S. 96. Egy \(\displaystyle D\) (\(\displaystyle 1\le D\le 10^{15}\)) hosszú rudat szeretnénk szétvágni \(\displaystyle N\) (\(\displaystyle 1\le N \le 500\;000\)) db kisebb rúdra. Tudjuk a kisebb rudak hosszát: az \(\displaystyle i\)-edik hossza \(\displaystyle r_i\) (\(\displaystyle 1\le r_i\le 10^{15}\)) és azt is tudjuk, hogy a kisebb rudak összhossza \(\displaystyle D\). Egy \(\displaystyle L\) hosszú rúd szétvágása tetszőleges hosszúságú két részre \(\displaystyle L\) forint. Egy vágással egyszerre csak egy rudat szabad kettévágni. Daraboljuk föl a lehető legolcsóbban a teljes \(\displaystyle D\) hosszú rudat a megadott \(\displaystyle r_i\) hosszú részekre.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle D\)-t, majd a következő \(\displaystyle N\) sorból az \(\displaystyle r_i\) egészeket, majd írja a standard output első sorába a minimális pénzt, amennyivel megoldható a szétdarabolás.

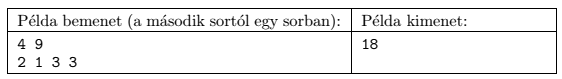
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Beküldendő egy tömörített s96.zip állományban a program forráskódja (s96.pas, s96.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s96.txt, s96.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2015. március 10-én LEJÁRT.

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Csenger Géza, Juhász 326 Dániel, Weisz Ambrus, Zalavári Márton, Zarándy Álmos.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2015. februári informatika feladatai