Az S. 99. feladat (2015. május)

S. 99. Egy \(\displaystyle M\) (\(\displaystyle 1\le M\le 100\;000\), \(\displaystyle M\) egész szám) hosszú falon \(\displaystyle N\) (\(\displaystyle 1\le N\le 5000\)) repedés keletkezett. Az egyszerűség kedvéért a repedéseket mint pontokat képzeljük el a falon, helyüket a fal egyik végétől valamilyen \(\displaystyle x\) (\(\displaystyle 1\le x\le M\), egész) koordináták adják meg. Célunk az, hogy lefessük a fal minden repedését. Úgy festünk, hogy kinyitunk egy \(\displaystyle w\) feliratú doboz festéket, amely pontosan \(\displaystyle w\) hosszú falrész festésére alkalmas, majd a tartalmával lefestünk egy \(\displaystyle x_0\) és \(\displaystyle x_1\) koordinátákkal határolt falrészt (\(\displaystyle w=x_1-x_0+1\)). A kiválasztott tartományon belül természetesen lefestjük az ép falrészeket is -- akár többször is. Addig nyitunk ki újabb festékesdobozt és festünk, amíg minden repedést el nem tüntettünk. A festéshez minden \(\displaystyle w\) (\(\displaystyle 1\le w\le M\)) egész számra egy \(\displaystyle w\) feliratú, és ismert \(\displaystyle b_j\) árú doboz festék áll rendelkezésre. Egy hosszabb festés nem feltétlenül drágább, mint egy rövidebb, sőt egy nagyobb doboz festék ára lehet egy kisebb doboz festék árával egyenlő, vagy annál kisebb is. Fessük le a lehető legolcsóbban az összes repedést a falon. Ehhez egy típusú festékből akár többet is felhasználhatunk.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle M\)-et, majd a következő \(\displaystyle N\) sorból az \(\displaystyle a_i\) egészeket, azaz a repedések helyét. A következő \(\displaystyle M\) sorban rendre az egyes hosszokhoz tartozó festékes dobozok \(\displaystyle b_j\) ára szerepel. Írjuk a standard output első sorába a minimális pénzt, amennyiből a festés megoldható. Helytakarékosság miatt a bemenetben az \(\displaystyle N\), illetve az \(\displaystyle M\) sorban lévő számokat / jellel elválasztva egy sorba írtuk.

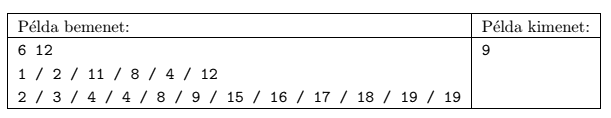
Magyarázat: ha veszünk egy 4, egy 1 és egy 2 feliratú vödröt, akkor azokkal pont le tudjuk festeni az összes repedést. Az ár: \(\displaystyle 4+2+3=9\).

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Beküldendő egy tömörített s99.zip állományban a program forráskódja (s99.pas, s99.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s99.txt, s99.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2015. június 17-én LEJÁRT.

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:	Gáspár Attila.
9 pontot kapott:	Németh 123 Balázs.
8 pontot kapott:	1 versenyző.
7 pontot kapott:	1 versenyző.
6 pontot kapott:	2 versenyző.
5 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2015. májusi informatika feladatai