KöMaL Problems in Physics, November 2021
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 15, 2021. |
M. 408. Let us make jam jar lids of different sizes collide with each other, such that one of them is at rest and the collision is a head on one. Determine the coefficient of restitution, which characterises the elasticity of the collision.
(6 pont)
 |
Problems with sign 'G'Deadline expired on December 15, 2021. |
G. 757. Suppose you have a pair of reversible gloves, both pieces black on the outside and white on the inside. Can you wear them as mismatched gloves?
(3 pont)
solution (in Hungarian), statistics
G. 758. An object is behind a car not very far from it, and its images can be seen in both side-view mirrors as well as in the rear-view mirror of the car. All the three mirrors are plane mirrors. In which mirror does the driver observe the greatest and the smallest image? In other words compare visual angles of the images.
(3 pont)
solution (in Hungarian), statistics
G. 759. Four balls of mass \(\displaystyle m\), then another four balls of \(\displaystyle M\) and then one more ball of mass \(\displaystyle m\) are strung on a horizontal, frictionless, fixed rod, as shown in the figure. The balls are close to each other, they are made of some perfectly elastic material and \(\displaystyle m <M\). From the left another ball of mass \(\displaystyle m\) is coming at a speed of \(\displaystyle v\) and collides with the first one of the ball string.
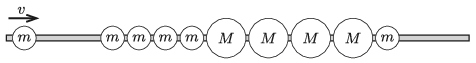
After the following collisions which balls remain at rest and what will the direction of the motion of the other balls be?
(4 pont)
solution (in Hungarian), statistics
G. 760. A 10 cm high aluminium cone is raised slowly out of an aquarium, by means of a thread attached to the apex of the cone. The shape of the aquarium is a rectangular box, and the diameter of the cone is also 10 cm. Initially the base of the cone lies on the bottom of the aquarium, and the cone is totally submerged into the water. The volume of the aquarium is much greater than that of the cone.
Plot the graph of the tension in the thread as a function of the displacement of the cone.
(4 pont)
 |
Problems with sign 'P'Deadline expired on December 15, 2021. |
P. 5355. Newspaper news (February 24, 2021): China's Mars probe, Tianwen-1, has been already orbiting Mars and has collected data from the red planet. The furthest point of its parking orbit measured from the surface of Mars is 59 thousand kilometres, while the nearest is 280 kilometres away. The probe makes one revolution around the planet in two Mars days.
By calculation check the accuracy of the value given for the period if the other data are accepted as correct.
(4 pont)
solution (in Hungarian), statistics
P. 5356. A beam of rectangular cross section lies on the horizontal ground. The horizontal side of the rectangle is \(\displaystyle L\), whilst its vertical side is \(\displaystyle H\). Neglecting air resistance, from which point and how should a grasshopper jump in order to jump over this beam with the least energy? In this case where is the focus of the parabolic path of the leap?
(5 pont)
solution (in Hungarian), statistics
P. 5357. A uniform-density rod is lying on a horizontal tabletop. The rod is slowly raised into the vertical position by a force which is exerted at one end of the rod always perpendicularly to the rod. What is the least value of the coefficient of static friction between the rod and the tabletop if the rod does not slip during the process?
(5 pont)
solution (in Hungarian), statistics
P. 5358. There are two beads on an insulated thin vertical thread, one of them is fixed and the other is held at a height of \(\displaystyle h = 0.5\) m above it.
The mass of the upper bead is \(\displaystyle m = 0.5\) grams and the charge of both beads is \(\displaystyle Q = 2.58\cdot 10^{-7}\) C. At a certain moment the upper bead is released without initial speed.
\(\displaystyle a\)) How much distance does the bead cover until it reaches its greatest speed?
\(\displaystyle b)\) What is this speed?
\(\displaystyle c)\) What will the least distance between the beads be?
\(\displaystyle d)\) What is the acceleration of the bead at the bottommost point of its path?
(4 pont)
solution (in Hungarian), statistics
P. 5359. The edges of a cube are built from resistors which has two different resistance values. The resistance of the resistors on 8 edges which are the edges of two opposite faces of the cube is \(\displaystyle r\), and the resistance of the other 8 resistors on the 4 edges perpendicular to the previously described edges is \(\displaystyle R\). Determine the equivalent resistance of the circuit between two adjacent vertices of the cube between which the resistance is \(\displaystyle R\).
(4 pont)
solution (in Hungarian), statistics
P. 5360. A simple Keplerian telescope is built for demonstration purposes. We have two converging lenses, one having a diameter of \(\displaystyle D\) and focal length \(\displaystyle f_1\), the other having a diameter of \(\displaystyle d\) and focal length \(\displaystyle f_2\) (\(\displaystyle f_1\gg f_2\), \(\displaystyle D>d\)), and we also have a shutter (a device that allows light to pass for a determined period) which can be fixed in the tube of the telescope at the common focal plane of the lenses. With the shutter we would like to control the direction of light rays forming the image.
\(\displaystyle a)\) What is the viewing angle of the telescope without the shutter? (That is: what is the maximum of the angular distance between two stars which can be seen in the telescope at the same time?)
\(\displaystyle b)\) At most what can the diameter of the shutter, which restricts the field of view of the telescope, be in order that the image should not get distorted (that is: the light rays determined by the directions of the rim of the image and pass the objective lens, also pass the eyepiece)?
\(\displaystyle c)\) Thus what can the field of view of the telescope be?
Hint: investigate how the parallel rays coming from different directions travel through the telescope.
(5 pont)
solution (in Hungarian), statistics
P. 5361. The following two photos were taken of the same car, at the same time. In the first photo the car was photographed through a curtain and in the second without the curtain. The car was at a distance of 20 metres from the curtain.

How densely woven could the curtain be?
(5 pont)
solution (in Hungarian), statistics
P. 5362. In a synchrocyclotron, the velocity dependence of the mass of elementary particles is compensated by decreasing the frequency of the electric field, which accelerates the particles. For example, if protons are accelerated, frequency of the applied voltage between the dees (D-shaped, metal, hollow half-discs) are varied from 25 MHz to 18.9 MHz in each cycle. Determine in this case
\(\displaystyle a)\) the magnitude of the magnetic induction;
\(\displaystyle b)\) the kinetic energy of the exiting protons.
(5 pont)
solution (in Hungarian), statistics
P. 5363. An hourglass was made from a thin, tall glass tube. The mass \(\displaystyle m_0\) of the sand in it is equal to the total mass of the glass tube and the supporting stands. Initially, the sand is at the bottom filling it up to a height of \(\displaystyle h=5\) cm. After turning the hourglass upside down the sand flows down at a steady rate in \(\displaystyle t_0=1\) minute. (Approximate the shape of the sand in the upper and lower bulbs with cylinders.)

\(\displaystyle a)\) Determine where the centre of gravity of the hourglass is time \(\displaystyle t\) after the clock was started. (Don't deal with the very short periods following the start of the hourglass or immediately before its stop, when the flow of sand does not or no longer fill the entire distance between the outlet and the lower impact point.)
\(\displaystyle b)\) Calculate the linear momentum of the hourglass time \(\displaystyle t\) after starting the hourglass.
\(\displaystyle c)\) We measured the weight of the hourglass with a very sensitive scale while the sand is flowing from the top cylinder to the bottom. We found that the weight measured is slightly greater than the weight of the hourglass that has already been stopped. Using your answers given to the previous two subtasks, determine how many thousandths of the weight of a working hourglass is greater than that of the already ``expired'' hourglass!
(6 pont)
Upload your solutions above.
