KöMaL Problems in Physics, December 2021
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 17, 2022. |
M. 409. Let us make a sponge cake. Measure the density of the dough before baking and after baking. Investigate how the density of the finished sponge cake varies depending on whether it was baked on the edge of the cake pan or in the middle. (Enter the sponge cake recipe as well.)
(6 pont)
 |
Problems with sign 'G'Deadline expired on January 17, 2022. |
G. 761. How was the word ``HÁTULJA'' (meaning BACK) written on the back of KöMaL: as usual or in mirror writing?

(3 pont)
solution (in Hungarian), statistics
G. 762. The photo on the left shows a garden solar shower. The incident sunlight heats up the water in the vertical black container. From the lower tap (the so-called leg wash) only cold water flows, while from the upper shower rose we can enjoy the water jet, whose temperature can be set with a single-lever shower mixer positioned in the middle. For the operation of the shower cold water flows in at the bottom. The structure of a shower without a foot wash is shown in the figure on the right. Complete the diagram with a foot wash, then explain how the garden shower works.
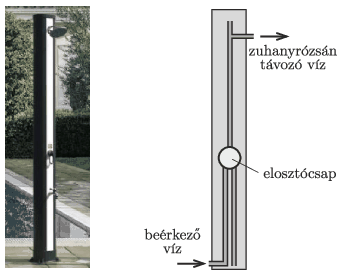
(4 pont)
solution (in Hungarian), statistics
G. 763. We have two solid cubes, one made of aluminium and the other made of copper. Placed on a particularly accurate scale they are both measured to be 1 ton to the nearest gram in vacuum. What will the difference between the results of the measurements be if the masses of the cubes are measured in air at standard temperature and pressure (STP)?
(4 pont)
solution (in Hungarian), statistics
G. 764. An object was released from rest and falls freely. It covered the same distance in the last second of its motion as it did in the first three seconds. From what height did it fall? (Neglect air resistance.)
(4 pont)
 |
Problems with sign 'P'Deadline expired on January 17, 2022. |
P. 5364. A solid half cylinder of radius \(\displaystyle R\), and of mass \(\displaystyle m\) is lying at rest on a flat, horizontal, frictionless surface with its curved surface facing upwards. From the top of the half cylinder a small object of mass also \(\displaystyle m\), starts from rest and slides down frictionlessly. How much distance does this small object cover sliding on the surface of the cylinder until it leaves it?
(5 pont)
solution (in Hungarian), statistics
P. 5365. A homogeneous, thin rod of length \(\displaystyle \ell\), mass \(\displaystyle m\) is suspended by one of its ends. The rod displaced slightly from its equilibrium position is swung with period \(\displaystyle T_0=2\) s. Such a rod is called a seconds pendulum.
\(\displaystyle a)\) What is the length of the rods? A rigid frame jointed from such rods shown in the figure is then suspended at one of its corners. This five-pointed star can move freely in its plane about the point \(\displaystyle O\).
\(\displaystyle b)\) What is the oscillation period \(\displaystyle T\) of the five-pointed star displaced slightly from its equilibrium position?
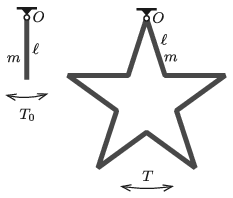
(5 pont)
solution (in Hungarian), statistics
P. 5366. The ratio of the specific heat capacity of an ideal gas at constant pressure to that of at constant volume is \(\displaystyle \kappa\).
\(\displaystyle a)\) The gas expands adiabatically. What is the ratio of the work done by the gas to the change in its internal energy?
\(\displaystyle b)\) The gas is compressed isothermally. What is the ratio of the work done by the gas to the absorbed heat by the gas?
\(\displaystyle c)\) The gas is heated and it undergoes isobaric expansion. What is the ratio of the work done by the gas to the heat absorbed by the gas?
(4 pont)
solution (in Hungarian), statistics
P. 5367. Two small metal balls are fixed at a distance of \(\displaystyle d\) on isolated rods, and both are given a charge of \(\displaystyle Q\).
\(\displaystyle a)\) Draw the sketch of the equipotential surfaces.
\(\displaystyle b)\) What is the potential of that surface which ``surrounds'' both charged balls?
(4 pont)
solution (in Hungarian), statistics
P. 5368. A ring made of a piece of metal wire with a radius of \(\displaystyle R=30\) cm is given a charge of \(\displaystyle Q=6\cdot10^{-6}\) C and then the ring is rotated in a vacuum at an angular velocity of \(\displaystyle \omega=520\) 1/s about an axis which is perpendicular to its plane and goes through the centre of the ring. At a certain moment an electron flies through the centre of the ring in the plane of the ring at a speed of \(\displaystyle v=120\) m/s. What is the radius of curvature of the orbit of the electron at the centre of the ring if there the magnetic field of the Earth points in the direction of the velocity of the electron?
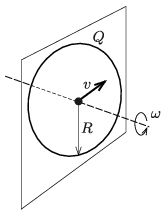
(5 pont)
solution (in Hungarian), statistics
P. 5369. There are two parallel metal rails in a horizontal plane, at a distance of \(\displaystyle \ell\). The left ends of the rails are connected with a resistor of resistance \(\displaystyle R\) and a switch as shown in the figure. The arrangement is in vertical uniform magnetic field which varies with time according to the following relation: \(\displaystyle B(t)=B_0+kt\), where \(\displaystyle B_0\) and \(\displaystyle k\) are known constants.
Perpendicular to the rails, a metal rod is placed at a distance of \(\displaystyle d\) from the switch, to the right side of the switch. The resistance of the rails and the metal rod is negligible. At time \(\displaystyle t=0\) the switch is closed and we begin to move the rod in the horizontal plane perpendicularly to the rod, at a constant speed of \(\displaystyle v_0\). Determine the current flowing in the rod at time \(\displaystyle t\).
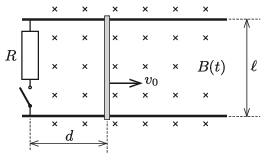
(5 pont)
solution (in Hungarian), statistics
P. 5370. The near point of the eye of a short-sighted person is at a distance of 8 cm from his eye, without wearing glasses. What will the distance of the near point of his eye be when he wears his \(\displaystyle -5\) dioptre glasses?
(4 pont)
solution (in Hungarian), statistics
P. 5371. The electric charge of a tau particle is the same as the electric charge of an electron. Its mass is 3470 times more than that of the electron, and 1.89 times more that of the proton. Its lifetime is very short (\(\displaystyle 3\cdot 10^{-13}\) s), but it may occur that it forms a bound system with a proton. In this case the two particles revolve in circular orbit around their common centre of mass, and the total angular momentum of the system is \(\displaystyle n\hbar\) \(\displaystyle (n=1,2,\ldots)\).
\(\displaystyle a)\) Determine the ratio of the wavelengths of the corresponding spectral lines of the \(\displaystyle \tau\)-proton atom and the hydrogen atom.
\(\displaystyle b)\) What is the binding energy of the \(\displaystyle \tau\)-proton atom?
(5 pont)
solution (in Hungarian), statistics
P. 5372. The natural angular frequency of a physical pendulum made of a rod (a rigid uniform-density rod pivoted at one end) is \(\displaystyle \omega\). In the steady state of the oscillation, what is the amplitude of the oscillation of the bottom end of the rod if the pivoted end of the pendulum is moved horizontally with a displacement, which varies with time according to the following formula: \(\displaystyle x(t) = A\cos {(2\omega t)}\)? Air resistance is small but not negligible and \(\displaystyle A\omega ^2\ll g\).
(6 pont)
Upload your solutions above.
