A KöMaL 2024. februári matematika feladatai

K-jelű feladatok A beküldési határidő 2024. március 11-én LEJÁRT.

---

K. 799. Misi egy olyan utcában lakik, amelyben csupa családi ház van. Ha az utca elejétől elindulunk, és megszámoljuk, hogy Misiék azon az oldalon hányadik házban laknak, akkor pontosan kétszer akkora eredményt kapunk, mint ha azt számoljuk meg, hogy az utca végétől számítva hányadik házban laknak. Az utcában a házakat az utca elejétől kezdve folyamatosan számozzák 1-től úgy, hogy a páratlan számú házak a bal oldalon, a páros számú házak a jobb oldalon vannak. Misiék az utca elejétől indulva a bal oldalon laknak. Ha az utca végétől kezdve számoznák a házakat, akkor Misiék házszáma 25-tel lenne kisebb, mint amennyi jelenleg. Hány ház van Misiék oldalán az utcában összesen?

(5 pont)

megoldás, statisztika

---

K. 800. Négy különböző pozitív prímszám összege \(\displaystyle 50\). Melyik négy prímszám lehet ez?

(5 pont)

megoldás, statisztika

---

K. 801. Az alábbi két edénynek oldalról nézve olyan alakja van, mint egy-egy betűnek. Az edények oldalnézeti képe látható a másik ábrán, egy 10 cm oldalhosszúságú négyzetekből álló rács elé állítva. Az edények felül nyitottak, vastagságuk \(\displaystyle 10\) cm. Mindkettőbe belehelyezünk egy-egy vékony kis gumicsövet, amelyek leérnek az aljukig, és ezeken keresztül vízzel töltjük meg mindkét edényt. Percenként \(\displaystyle 1\) liter víz folyik be a csövön keresztül mindegyik edénybe. Hány perc alatt telik meg az egyik, illetve a másik edény? Ábrázoljuk az egyes edényekben lévő víz magasságának időbeli alakulását grafikonon. (Az edények falának vastagságát hagyjuk figyelmen kívül.)

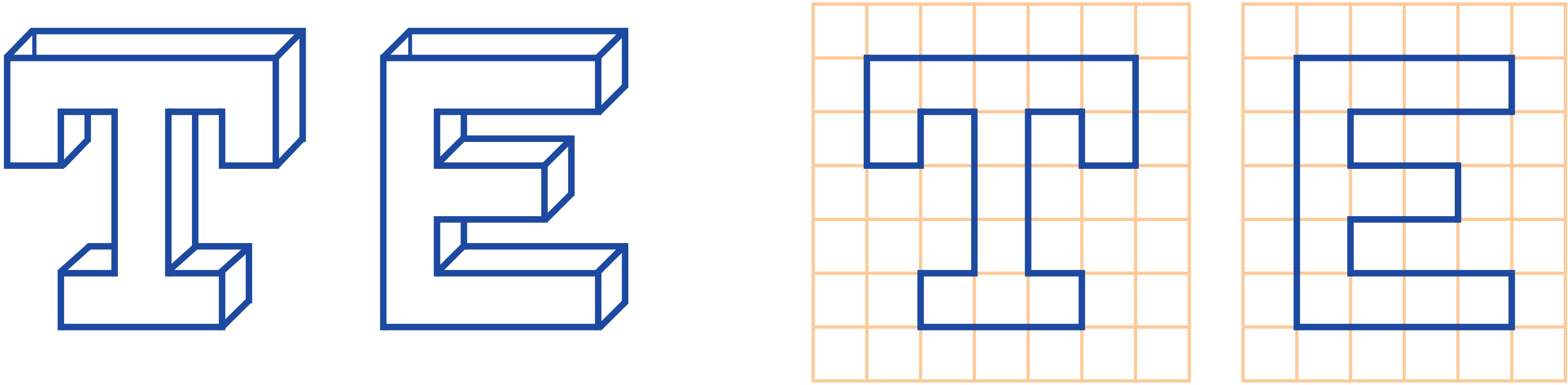
(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2024. március 11-én LEJÁRT.

---

K/C. 802. Legyen az \(\displaystyle ABCD\) négyzet \(\displaystyle CD\) oldalának tetszőleges belső pontja \(\displaystyle Q\). Az \(\displaystyle AQ\) egyenesre állítsunk merőlegest a \(\displaystyle B\) csúcsból, legyen ennek \(\displaystyle AQ\)-val vett metszéspontja \(\displaystyle P\). Legyen továbbá a négyzet átlóinak metszéspontja \(\displaystyle K\). Mutassuk meg, hogy a \(\displaystyle PK\) egyenes felezi a \(\displaystyle QPB\) szöget.

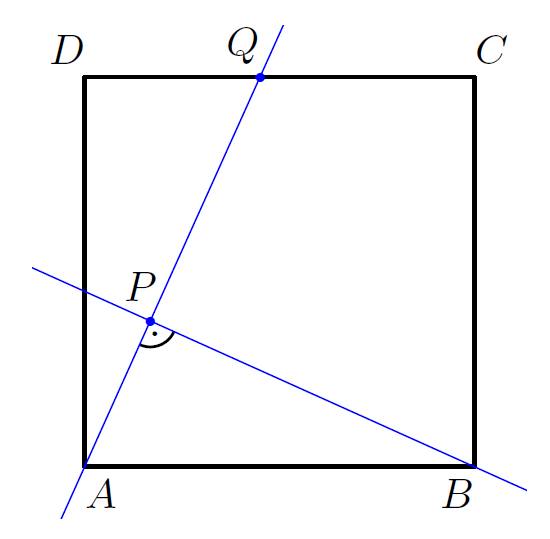
(5 pont)

megoldás, statisztika

---

K/C. 803. Egy táborban \(\displaystyle 24\) gyerek kivételével mindenki egyke (nincs testvére), \(\displaystyle 18\) gyerek kivételével mindenkinek egy testvére van, \(\displaystyle 14\) gyerek kivételével pedig mindenkinek két testvére van. Hányan lehetnek azok ebben a táborban, akiknek \(\displaystyle 2\)-nél több testvérük van, ha tudjuk, hogy van legalább egy egyke, és mindenkinek az összes testvére is ott nyaral a táborban?

Javasolta: Kozma Katalin Abigél (Győr), Korándi József (Budapest)

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2024. március 11-én LEJÁRT.

---

C. 1798. Határozzuk meg a

\(\displaystyle \left(p+\frac{1}{p}\right)\cdot\left(x-\frac{1}{x}\right)+\left(p-\frac{1}{p}\right)\cdot\left(x+\frac{1}{x}\right)=4px+5+\frac{1}{p} \)

egyenlet összes egész megoldását, ha a \(\displaystyle p\) paraméter egész szám.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1799. Az egységnyi oldalú \(\displaystyle ABCD\) négyzetben megrajzoltuk a \(\displaystyle DEFG\), \(\displaystyle AHKE\), \(\displaystyle BMFL\) és \(\displaystyle CGNP\) négyzeteket az ábra szerint.

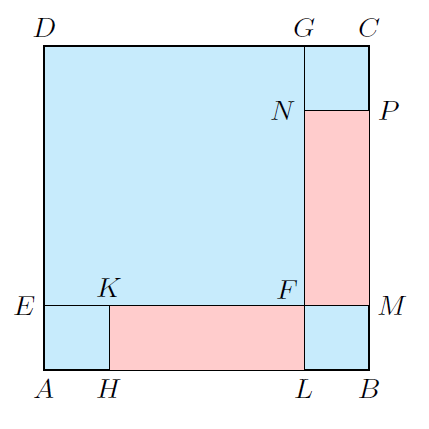
Az \(\displaystyle LFKH\) és \(\displaystyle MPNF\) téglalapok területének összege legfeljebb hányadrésze lehet az \(\displaystyle ABCD\) négyzet területének?

Adjuk meg ebben az esetben az \(\displaystyle \dfrac{ED}{AD}\) arány pontos értékét.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1800. Mutassuk meg, hogy ha \(\displaystyle n\) természetes szám, akkor a

\(\displaystyle \Bigl[\sqrt{16n+21}; \sqrt{16n+24}\Bigr] \)

intervallumban nincs egész szám.

Javasolta: Holló Gábor (Budapest)

(5 pont)

megoldás, statisztika

---

C. 1801. Legyen az \(\displaystyle a_n\) sorozat a következő: \(\displaystyle a_1=2\) és \(\displaystyle a_n=a_{n-1}+2n\). Mennyi a sorozat első \(\displaystyle 2024\) tagjának reciprokösszege? (Vagyis mennyi az \(\displaystyle \frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+ \dots +\frac{1}{a_{2024}}\) kifejezés értéke?)

Javasolta: Szmerka Gergely (Budapest)

(5 pont)

megoldás, statisztika

---

C. 1802. Az \(\displaystyle ABCDEF\) szabályos hatszögben \(\displaystyle M\) az \(\displaystyle AC\), \(\displaystyle N\) pedig a \(\displaystyle CE\) átló belső pontja úgy, hogy

\(\displaystyle \frac{AM}{AC}=\frac{CN}{CE}=k. \)

A \(\displaystyle k\) szám milyen értékeire lesznek a \(\displaystyle B\), \(\displaystyle M\) és \(\displaystyle N\) pontok kollineárisak?

Matlap, Kolozsvár (2017)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2024. március 11-én LEJÁRT.

---

B. 5366. Van-e olyan \(\displaystyle n>1\) összetett egész szám, amely rendelkezik a következő tulajdonsággal: ha \(\displaystyle 1=d_1<d_2<\ldots<d_k=n\) jelölik \(\displaystyle n\) pozitív osztóit, akkor \(\displaystyle d_i\) osztható \(\displaystyle (d_{i-1}+d_{i-2})\)-vel minden \(\displaystyle 3\leq i\leq k\) esetén?

(IMO 2023/1 módosítása)

(3 pont)

megoldás, statisztika

---

B. 5367. \(\displaystyle a)\) Az egységnyi sugarú nyílt körlapban elhelyeztünk egymásra merőlegesen két \(\displaystyle \ell\) hosszúságú nyílt szakaszt úgy, hogy a szakaszoknak nincs közös pontjuk. Mennyi lehet \(\displaystyle \ell\)?

\(\displaystyle b)\) Az egységnyi sugarú nyílt gömbben elhelyeztünk három \(\displaystyle \ell\) hosszúságú nyílt szakaszt úgy, hogy páronként merőlegesek, és semelyik kettőnek nincs közös pontja. Mennyi lehet \(\displaystyle \ell\)?

Javasolta: Vígh Viktor (Sándorfalva)

(4 pont)

megoldás, statisztika

---

B. 5368. Egy pingpongbajnokságon teljes körmérkőzést játszottak, azaz mindenki mindenkivel pontosan egyszer játszott. A győzelemért \(\displaystyle 1\), a vereségért \(\displaystyle 0\) pont járt (döntetlen nincs a pingpongban). Érdekes módon volt egy olyan játékos, aki pontosan azokat az ellenfeleit győzte le, akik nála több pontot szereztek a bajnokság végére, és pontosan azoktól kapott ki, akik nála kevesebb pontot szereztek.

Legalább hány résztvevője lehetett a bajnokságnak?

(Lehetséges, hogy több versenyzőnek is ugyanannyi pontja lett a verseny végén. A bajnokságon legalább ketten vettek részt.)

Javasolta: Nagy Kartal (Budapest) és Hujter Bálint (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5369. Az \(\displaystyle ABC\) szabályos háromszög \(\displaystyle P\) belső pontjára \(\displaystyle APB\sphericalangle=150^\circ\). Mutassuk meg, hogy \(\displaystyle PA^2+PB^2=PC^2\).

Javasolta: Vígh Viktor (Sándorfalva)

(4 pont)

megoldás, statisztika

---

B. 5370. Legyen \(\displaystyle k\) pozitív egész, és tegyük fel, hogy az \(\displaystyle a_1,\ldots, a_k\) valós számokra \(\displaystyle \sum_{i=1}^k (k-i+1) a_i=0\). Mutassuk meg, hogy van olyan \(\displaystyle m\le k\) pozitív egész szám, amelyre

\(\displaystyle 2m\sum_{i=1}^{m} a_i\le \sum_{i=1}^m i a_i. \)

Javasolta: Vígh Viktor (Sándorfalva)

(5 pont)

megoldás, statisztika

---

B. 5371. Legyen \(\displaystyle P\) pont az \(\displaystyle ABC\) háromszög belső pontja. Jelölje a \(\displaystyle P\) pont merőleges vetületét a \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalakra rendre \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\). Bizonyítsuk be, hogy

\(\displaystyle \frac{PE+PF}{PA}+\frac{PF+PD}{PB}+\frac{PD+PE}{PC}\le 3. \)

Javasolta: Bencze Mihály (Brassó)

(5 pont)

megoldás, statisztika

---

B. 5372. Egy gömb felszínét néhány főkörrel gömbi háromszögekre és négyszögekre daraboltuk úgy, hogy semelyik három főkör nem megy át egy ponton, továbbá keletkezett legalább egy négyszög. Mutassuk meg, hogy pontosan nyolc gömbháromszöget és hat gömbi négyszöget kaptunk.

Javasolta: Vígh Viktor (Sándorfalva)

(6 pont)

megoldás, statisztika

---

B. 5373. Legyen \(\displaystyle n\) pozitív egész szám. Igazoljuk, hogy az \(\displaystyle a_{7n}x^{7n}+\dots+a_1x+a_0=(x^7+x^6+x^5+x^4+x^3+x^2+x+1)^n\) polinom páratlan együtthatóinak száma legalább 8.

Javasolta: Pach Péter Pál (Budapest)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2024. március 11-én LEJÁRT.

---

A. 872. Minden \(\displaystyle k\) pozitív szám esetén legyen \(\displaystyle a_{k,1}\), \(\displaystyle a_{k,2}\), \(\displaystyle \ldots\) egy pozitív egész számokból álló sorozat. Minden \(\displaystyle k\) pozitív egész szám esetén legyen az \(\displaystyle \{a_{k+1,i}\}\) sorozat az \(\displaystyle \{a_{k,i}\}\) sorozat különbségsorozata, azaz minden \(\displaystyle k\) és \(\displaystyle i\) pozitív egészre teljesül, hogy \(\displaystyle a_{k,i+1}-a_{k,i}=a_{k+1,i}\).

Lehetséges-e, hogy minden pozitív egész pontosan egyszer szerepel az \(\displaystyle a_{k,i}\) számok között?

Javasolta Matolcsi Dávid (Berkeley)

(7 pont)

megoldás, statisztika

---

A. 873. Az \(\displaystyle ABCD\) egy konvex húrnégyszög, melyben \(\displaystyle AB\cdot CD=AD\cdot BC\) teljesül. Az \(\displaystyle ABC\) háromszög \(\displaystyle I\) középpontú \(\displaystyle \omega\) beírt köre a \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalakat rendre az \(\displaystyle A'\), \(\displaystyle B'\) és \(\displaystyle C'\) pontokban érinti. Legyen \(\displaystyle K\) az \(\displaystyle ID\) egyenes és az \(\displaystyle A'B'C'\) háromszög Feuerbach-körének azon metszéspontja, amely az \(\displaystyle ID\) szakasz belsejében van.

Mutassuk meg, hogy ha \(\displaystyle S\) az \(\displaystyle A'B'C'\) háromszög súlypontja, akkor az \(\displaystyle SK\) egyenes és a \(\displaystyle BB'\) egyenes \(\displaystyle \omega\)-n metszi egymást.

Javasolta Bán-Szabó Áron (Budapest)

(7 pont)

megoldás, statisztika

---

A. 874. Nyihaha és Bruhaha két egymás melletti sziget, mindkettőn \(\displaystyle n\) ember él.

Nyihaha lakói mind Lovagok, akik mindig igazat mondanak, vagy Lókötők, akik mindig hazudnak. Bruhaha lakói normális emberek, akik azt modnanak amit akarnak. Mindkét szigeten hagyomány egy rituálé: amikor egy hajós érkezik a szigetre, akkor minden lakó véletlenszerűen (egyenletes eloszlással és egymástól függetlenül) rámutat egy másik szigetlakóra, és azt mondja ,,Ő Lovag'' vagy ,,Ő Lókötő''. Nyihaha szigetén a Lovagok az igazat, a Lókötők hazugságot mondanak arról, akire mutatnak. Bruhaha szigetén pedig mindenki, egymástól függetlenül \(\displaystyle 1/2\) valószínűséggel mondja ezt vagy azt.

Szindbád megérkezik Bruhaha szigetére, de eredetileg nem tudja, melyik szigeten van. Megfigyelve a rituálét, \(\displaystyle p_n\) valószínűséggel lát olyat, amiből egyértelműen meg tudja állapítani, hogy nem Nyihahán van. Igaz-e, hogy \(\displaystyle p_n \to 1\), ha \(\displaystyle n\to \infty\)?

Javasolta Matolcsi Dávid (Berkeley)

(7 pont)

megoldás, statisztika