KöMaL Problems in Mathematics, May 2024
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on June 10, 2024. |
K. 814. EOn a field, a flock of sheep is grazing. Some of the sheep have been marked, and the ratio of marked to unmarked sheep is \(\displaystyle {\frac{3}{5}}\). Only 17 of the unmarked sheep have been sheared, and all the marked sheep have been sheared, however, the number of sheared and unsheared sheep is equal. Find the number of sheep grazing on the field.
Proposed by: Bíró Bálint (Eger)
(5 pont)
solution (in Hungarian), statistics
K. 815. Point \(\displaystyle D\) is chosen on leg \(\displaystyle BC\) of right triangle \(\displaystyle ABC\) satisfying \(\displaystyle BC=4BD\), and point \(\displaystyle E\) is chosen on leg \(\displaystyle AC\) satisfying \(\displaystyle AC=8CE\). Find the length of hypotenuse \(\displaystyle AB\) given that \(\displaystyle AD=164\) and \(\displaystyle BE=52\).
Vietnamese problem
(5 pont)
solution (in Hungarian), statistics
K. 816. Expression \(\displaystyle {E(x)=\frac{8x-12}{4x^2-12x+9}-\frac{5x}{2x^2+3x}-\frac{20x}{9-4x^2}}\) is given. Find integers \(\displaystyle x\) for which \(\displaystyle E(x)\) is a natural number.
Matlap (Kolozsvár)
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on June 10, 2024. |
K/C. 817. There are four pieces of paper in a box, and a positive number is written on each of them. We choose some of them from the box in all possible ways, and take the sum of the numbers on the papers. (If we choose a single piece of paper, we take the number that is written on the paper.) Find the numbers written on the papers, if the sums are always consecutive integer numbers.
(5 pont)
solution (in Hungarian), statistics
K/C. 818. In the right triangle \(\displaystyle ABC\) the lengths of the legs are \(\displaystyle BC=6\) and \(\displaystyle CA=8\). Let \(\displaystyle P\) and \(\displaystyle Q\) denote the trisection point closer to \(\displaystyle B\) and the midpoint of leg \(\displaystyle BC\), respectively, let \(\displaystyle R\) and \(\displaystyle S\) denote the trisection point closer to \(\displaystyle C\) and the midpoint of leg \(\displaystyle CA\), respectively, and finally let \(\displaystyle T\) and \(\displaystyle U\) denote the trisection point closer to \(\displaystyle A\) and the midpoint of hypotenuse \(\displaystyle AB\), respectively. Reflect trisection points \(\displaystyle P\), \(\displaystyle R\) and \(\displaystyle T\) across the other endpoints of the respective sides according to the diagram.
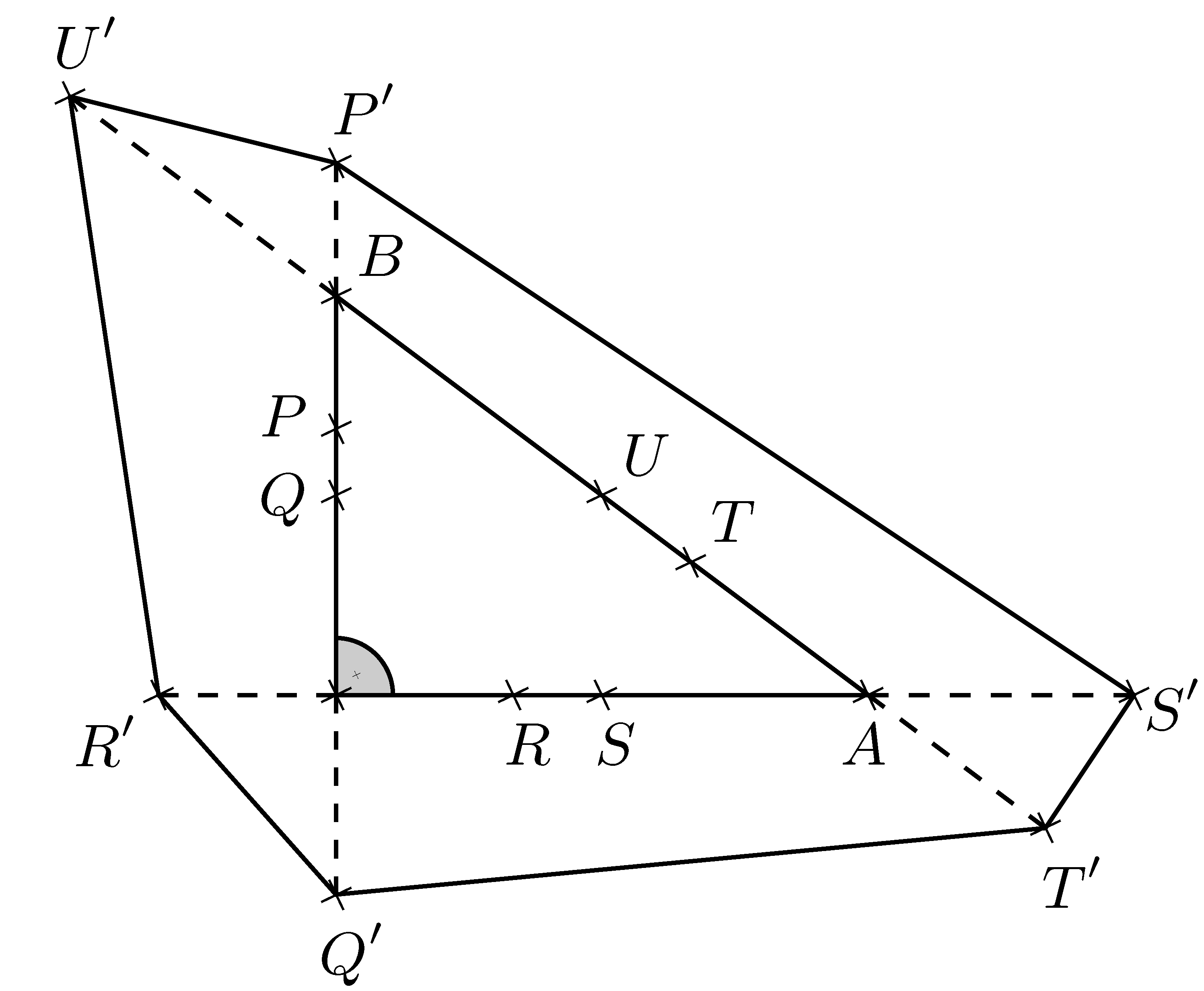
Find the area of polygon \(\displaystyle P'U'R'Q'T'S'\).
Proposed by: Bíró Bálint, (Eger)
(5 pont)
 |
Problems with sign 'C'Deadline expired on June 10, 2024. |
C. 1813. Prove that there exist no positive integers \(\displaystyle m\) and \(\displaystyle n\), for which \(\displaystyle 3^{m}+3^{n}+1\) is a perfect square.
USA competition problem
(5 pont)
solution (in Hungarian), statistics
C. 1814. A circle with radius \(\displaystyle r\) is divided into two parts with a line that has a distance of \(\displaystyle \displaystyle{\frac{r}{\sqrt{2}}}\) from the center of the circle. Find the ratio of the areas of the two parts.
Proposed by András Ringler (Budapest)
(5 pont)
solution (in Hungarian), statistics
C. 1815. Solve the following system of equations for natural numbers \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) and \(\displaystyle u\): \(\displaystyle x^2y-zu^2=6\), \(\displaystyle x^2z+yu^2=11\).
Based on an idea of Sándor Katz, Bonyhád
(5 pont)
solution (in Hungarian), statistics
C. 1816. Let the sides of a triangle with side lengths \(\displaystyle a=14\), \(\displaystyle b=13\), \(\displaystyle c=15\) be tangent to a sphere with radius \(\displaystyle R=5\). Find the distance between the center of the sphere and the plane of the triangle.
(Croatian competition problem)
(5 pont)
solution (in Hungarian), statistics
C. 1817. We have tossed a coin several times. The sequence of results turned out to be one head, one tail, one head, two tails, one head, three tails, and so on (each time the lengths of the contiguous segments of tails increase by one separated by a single head). Assuming this regularity, after how many tosses will the relative frequency of the heads be exactly \(\displaystyle \frac{1}{2023}\)?
(Proposed by Mátyás Barczy, Gábor Nyul, Debrecen)
(5 pont)
 |
Problems with sign 'B'Deadline expired on June 10, 2024. |
B. 5390. Is it possible to find even integers \(\displaystyle a_0\), \(\displaystyle a_1\), \(\displaystyle \ldots\), \(\displaystyle a_{n-1}\) for which polynomial \(\displaystyle x^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0\) is divisible by \(\displaystyle x^2+x+1\)?
(Proposed by Géza Kós, Budapest)
(3 pont)
solution (in Hungarian), statistics
B. 5391. Let \(\displaystyle C\) be a point on a circle with unit diameter \(\displaystyle AB\). Let points \(\displaystyle D\) and \(\displaystyle E\) be chosen on line segment \(\displaystyle AB\) such that \(\displaystyle BD = BC\) and \(\displaystyle AE = AC\). Find the smallest possible value of \(\displaystyle AD^2 + DE^2 + EB^2\).
(Proposed by József Szoldatics, Budapest)
(4 pont)
solution (in Hungarian), statistics
B. 5392. Let us consider a trapezoid whose area is equal to the product of the lengths of its bases. Prove that this trapezoid is tangential if and only if it is right.
(Proposed by László Németh, Fonyód)
(5 pont)
solution (in Hungarian), statistics
B. 5393. Let \(\displaystyle f\) be a real function (that is, a real-valued function of a real variable) satisfying \(\displaystyle \left|f(x+y+z)+\sin x+\sin y+\sin z \right|\le 3\), for all \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\in \mathbb{R}\). Prove that \(\displaystyle |f(x)-\sin x|\le 1\) for all \(\displaystyle x\in \mathbb{R}\).
(Proposed by Mihály Bencze, Brasov)
(4 pont)
solution (in Hungarian), statistics
B. 5394. Let \(\displaystyle O\) be the center of square \(\displaystyle ABCD\), and let \(\displaystyle X\) be an arbitrary point on its circumcircle. Let \(\displaystyle T\) denote the orthogonal projection of \(\displaystyle X\) onto \(\displaystyle BC\). Let \(\displaystyle E\) denote the intersection of lines \(\displaystyle XB\) and \(\displaystyle AC\), and let \(\displaystyle F\) denote the intersection of lines \(\displaystyle XC\) and \(\displaystyle BD\). Prove the \(\displaystyle EF\) is perpendicular to \(\displaystyle TO\).
(Proposed by Viktor Vígh, Sándorfalva)
(4 pont)
solution (in Hungarian), statistics
B. 5395. Let \(\displaystyle d(k)\) denote the number of positive divisors of a positive integer \(\displaystyle k\), and let \(\displaystyle 1<n\) be an integer. Which sum is larger: \(\displaystyle d(2)+d(4)+\dots+d(2n)\) or \(\displaystyle (d(1)+d(3)+\dots+d(2n-1))+(d(1)+d(2)+\dots+d(n))\)?
(Proposed by Péter Pál Pach, Budapest)
(5 pont)
solution (in Hungarian), statistics
B. 5396. An equilateral pentagon in the three-dimensional space has four right angles. What can be its fifth angle?
(Proposed by Péter Dombi, Pécs)
(6 pont)
solution (in Hungarian), statistics
B. 5397. Let \(\displaystyle G\) be a graph (possibly with multiple edges) with the following property: whenever the vertices of \(\displaystyle G\) are partitioned into \(\displaystyle t\) disjoint sets, there are at least \(\displaystyle 2t-2\) edges connecting different sets. Show that the edges of \(\displaystyle G\) can be colored red or blue such that the red edges and the blue edges each form a connected graph (and reaching all the vertices).
(Proposed by Kada Williams, Cambridge)
(6 pont)
 |
Problems with sign 'A'Deadline expired on June 10, 2024. |
A. 881. We visit all squares exactly once on a \(\displaystyle n\times n\) chessboard (colored in the usual way) with a king. Find the smallest number of times we had to switch colors during our walk.
(Proposed by Dömötör Pálvölgyi, Budapest)
(7 pont)
A. 882. Let \(\displaystyle H_1\), \(\displaystyle H_2\), \(\displaystyle \ldots\), \(\displaystyle H_m\) be non-empty subsets of the positive integers, and let \(\displaystyle S\) denote their union. Prove that \(\displaystyle \sum_{i=1}^m \sum_{a, b\in H_i} \gcd(a,b) \ge \frac{1}{m} \sum_{a, b\in S} \gcd(a, b)\).
(The \(\displaystyle \sum_{(a,b)\in X}\) notation means that the summation is over ordered pairs \(\displaystyle (a,b)\) where \(\displaystyle a\in X\) and \(\displaystyle b\in X\).)
(Proposed by Dávid Matolcsi, Berkeley)
(7 pont)
A. 883. Let \(\displaystyle J \subsetneq I \subseteq \mathbb{R}\) be non-empty open intervals, and let \(\displaystyle f_1\), \(\displaystyle f_2\), \(\displaystyle \ldots\) be real polynomials satisfying the following conditions:
- \(\displaystyle f_i(x) \geq 0\) for all \(\displaystyle i \geq 1\) and \(\displaystyle x \in I\),
- \(\displaystyle \sum_{i=1}^\infty f_i(x)\) is finite for all \(\displaystyle x \in I\),
- \(\displaystyle \sum_{i=1}^\infty f_i(x)=1\) for all \(\displaystyle x \in J\).
Do these conditions imply that \(\displaystyle \sum_{i=1}^\infty f_i(x)=1\) also for all \(\displaystyle x \in I\)?
(Proposed by András Imolay, Budapest)
(7 pont)
Upload your solutions above.
