Fórum: Háromszög szerkesztés

Az előző hozzászólás második ábrája:

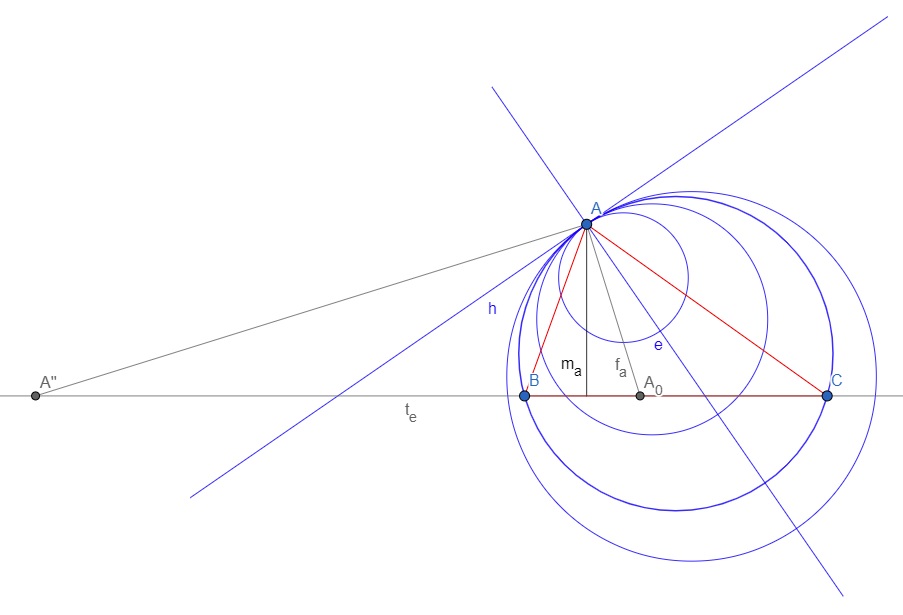
Egy másik, szintén körsoron alapuló megoldás kínálkozik hihetetlen[7] észrevétele alapján: Az $\displaystyle m_a$ magasság egyenesét $\displaystyle f_a$ -ra tükrözve a kapott $\displaystyle e$ egyenes átmegy a körülírt $\displaystyle k$ kör középpontján. $\displaystyle k$ tehát eleme annak a parabolikus körsornak, melynek $\displaystyle A$ a pontköre és $\displaystyle e$ a centrálisa, $\displaystyle h$ hatványvonala az $\displaystyle e$ -re $\displaystyle A$ -ban emelt merőleges. A körsornak azt a körét kell megszerkeszteni, amelyik $\displaystyle h$ -nak $\displaystyle f_a$ -t tartalmazó oldalán van és az adott BC hosszúságú húrja esik $\displaystyle t_e$ -re.

Legyen $\displaystyle t_e$ és $\displaystyle h$ metszéspontja $\displaystyle P$ . Vegyük fel $\displaystyle e$ -n az adott $\displaystyle B_0 C_0 = BC$ hosszúságú $\displaystyle AR$ szakaszt. Az $\displaystyle AR$ átmérőjű $\displaystyle k'$ kör középpontja $\displaystyle S$ . $\displaystyle k'$ a körsor eleme. A $\displaystyle PS$ egyenes és $\displaystyle k'$ metszéspontjai $\displaystyle T$ és $\displaystyle U$. $\displaystyle PT \cdotp PU = PA^2$. Forgassuk le $\displaystyle T$ -t és $\displaystyle U$ -t $\displaystyle P$ körül $\displaystyle t_e$ -re. A kapott pontokat véve $\displaystyle B$ -nek és $\displaystyle C$ -nek az $\displaystyle ABC$ háromszög és annak körülírt $\displaystyle k$ köre megfelel: $\displaystyle BC = TU = AR = B_0 C_0$ az adott oldalhossz, $\displaystyle PB \cdotp PC = PT \cdotp PU = PA^2$, $\displaystyle k$ a körsor eleme, középpontja $\displaystyle e$-n van, $\displaystyle m_a$ és $\displaystyle e$ szögfelezője, $\displaystyle f_a$ a $\displaystyle BAC$ szöget is felezi.

A második ábra a következő hozzászólásban.

Ujjgyakorlat: Hogyan értelmezhető a körsor $\displaystyle h$ -nak $\displaystyle f_a$ - val ellentétes oldalán lévő $\displaystyle k_2$ köre, melyből $\displaystyle t_e$ szintén $\displaystyle BC$ hosszúságú húrt metsz ki?

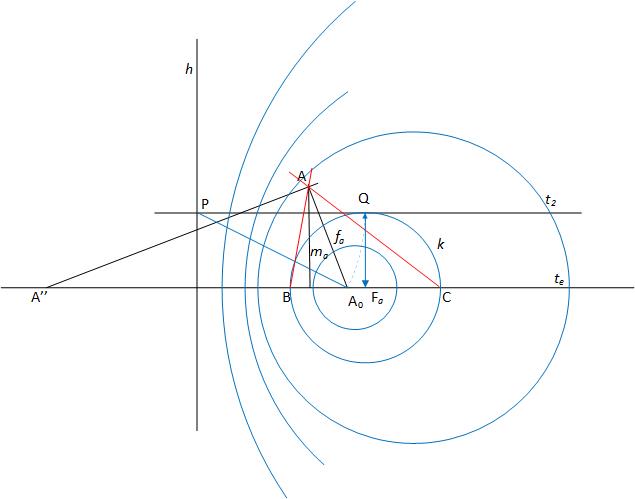
Hát igen. Inverzióra sincs is szükség. Az $\displaystyle A_0$ $\displaystyle A''$ pontpárhoz tartozó Apollóniusz körök elliptikus körsort alkotnak, melynek $\displaystyle A_0$ és $\displaystyle A''$ a pontkörei, $\displaystyle h$ hatványvonala $\displaystyle A_0$ $\displaystyle A''$ felező merőlegese. A keresett $\displaystyle BC$ átmérőjű $\displaystyle k$ körnek a $\displaystyle t_e$ egyenessel párhuzamos, attól BC/2 távolságra levő $\displaystyle t_2$ egyenes érintője. Jelöljük $\displaystyle t_2$ és $\displaystyle h$ metszéspontját $\displaystyle P$ -vel, a $\displaystyle k$ és $\displaystyle t_2$ érintési pontját $\displaystyle Q$ -val. $\displaystyle P$ a hatványvonalon van, a körsor köreire vonatkozó hatványa egyenlő, így az $\displaystyle A_0$ pontkörre vonatkozó hatványa egyenlő a $\displaystyle k$ -ra vonatkozó hatvánnyal, $\displaystyle {PA_0}^2 = {PQ}^2$ .

Innen a szerkesztés: A $\displaystyle P$ középpontú $\displaystyle PA_0$ sugarú körívvel kimetsszük $\displaystyle Q$ -t $\displaystyle t_2$ -ből. A $\displaystyle Q$ -ból $\displaystyle t_e$ -re bocsátott merőleges talppontja lesz a $\displaystyle BC$ oldal $\displaystyle F_a$ felezőpontja, $\displaystyle B$ -t és $\displaystyle C$ -t az $\displaystyle F_a$ középpontú $\displaystyle F_aQ = BC/2$ sugarú $\displaystyle k$ kör metszi ki $\displaystyle t_e$ -ből.

Na jó. Azon a részen, hogy egy Apollóniuszi körsornak egy adott méretű / egy adott egyenest érintő tagját keressük, lehet jó sokat egyszerűsíteni.

Egy megoldás inverzióval: ugyanúgy kezdődik, mint a Kömalban szereplő II megoldás: az $\displaystyle f_a$ szakasz $\displaystyle A_0$ végpontjából érintőegyenest húzunk az $\displaystyle f_a$ szakasz $\displaystyle A$ csúcsa körüli $\displaystyle m_a$ sugarú körhöz, a kapott $\displaystyle t_e$ egyenesen lesz a B és a C csúcsa a háromszögnek.

Legyen $\displaystyle A''$ az A csúcsbeli másik szögfelező metszése az előbbi $\displaystyle t_e$ egyenessel. A keresett B és C pontok inverz pontpárok $\displaystyle A_0$-ra és $\displaystyle A''$-re, a távolságuk meg van adva, már csak meg kell szerkeszteni őket.

Ez pedig történhet inverzióval: a BC pontpárokra Thalész köröket képzelünk, olyat keresünk, amelyik érinti a $\displaystyle t_e$ egyenessel párhuzamos, attól BC/2 távolságra levő egyeneseket, és merőleges $\displaystyle A_0A''$ Thalész-körére. Ennek a körnek a két metszéspontja a $\displaystyle t_a$ egyenessel lesz a keresett B és a C pont. Az egyik ilyen egyenest invertáljuk $\displaystyle A_0 A''$ Thalész-körére, kapjuk $\displaystyle q$ kört. Az inverzió a keresett BC talpppontú kört helybenhagyja, és érintkezést érintkezésbe visz, így már csak azt a kört kell megkeresni, amelyik érinti az előbbi két, $\displaystyle t_a$-val párhuzamos egyenest, és az egyiknek a q inverz képét; ami az Apollóniuszi probléma két egyenessel és egy darab körrel, a szerkesztés ismert.

Egyrészt csodálom, hogy ilyen gondosan tanulmányozod a régi feladatokat, másrészt remélem, hogy nem feltételezed rólam, hogy régi feladatok előbányászásával szeretnék hozzászólásokat provokálni, elmesélem a feladat történetét (én hogyan találkoztam vele):

A 90-es évek elején egyik fiam hozta haza a József Attila gimnáziumból. Úgy ítéltem, hogy nehezebb feladat, mint amit házi feladatnak szoktak adni, de felkeltette az érdeklődésemet, ezért aztán megpróbálkoztam a megoldásával. Több megoldást is kitaláltam, de mindegyik számolásos. Egy ilyet mindjárt le is írok. A megoldások nem túl elegánsak és nehezen szerkeszthetőek (terület átalakításokkal mindegyik szerkesztés elvégezhető volt), ezért időről-időre eszembe jutott, hogy kell lennie egyszerűbb megoldásnak is. Több matematikus ismerősömnek is elmeséltem, de nekik nem keltette fel az érdeklődésüket, vagy csak nem akartak elegendő időt fordítani a megoldásra. Egy éjszaka nyaralás közben jutott eszembe az a megoldás, amelyet már leírtam.

Most lássuk az egyik nem túl elegáns megoldást, amelyhez könnyen el lehet jutni (kiszámítjuk a háromszög köré írható kör sugarának hosszát)! A szerkesztést nem részletezem.

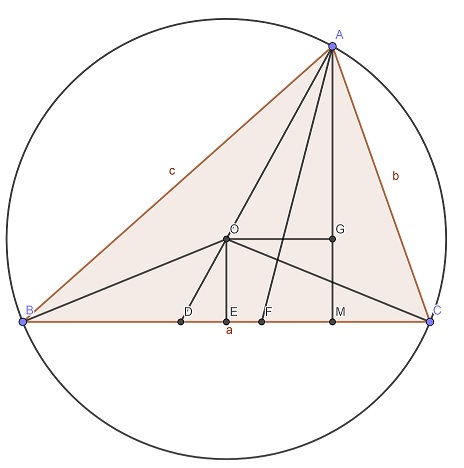
Legyen adva az $\displaystyle ABC$ háromszög $\displaystyle BC=a$ oldala, $\displaystyle AM=m$ a háromszög magassága és $\displaystyle AF=f$ a háromszög szögfelezője!

Tükrözzük át a magasságot a szögfelezőre! Ez az egyenes át fog menni a körülírható kör $\displaystyle O$ középpontján. A körülírható kör sugara legyen $\displaystyle r$ hosszúságú! Az egyenesnek a háromszögbe eső darabja $\displaystyle AD=l$. Bocsássunk merőlegest $\displaystyle O$-ból a $\displaystyle BC$ oldalra, ennek talppontja $\displaystyle E$ és $\displaystyle OE=x$! Bocsássunk merőlegest $\displaystyle O$-ból az $\displaystyle AM$ magasságra, ennek talppontja $\displaystyle G$!

Mivel $\displaystyle AOG\triangle\thicksim ADM\triangle$ ezért

$\displaystyle \frac{m-x}{r}=\frac{m}{l}$

A Pythagoras-tétel szerint

$\displaystyle x^2+\Big(\frac{a}{2}\Big)^2=r^2$

Az egyenletrendszerből $\displaystyle r$ meghatározható (a negatív gyök nem érdekel):

$\displaystyle r=\frac{-\frac{m^2}{l} + \sqrt{m^2 + \Big(\frac{a}{2}\Big)^2\Big(1-\frac{m^2}{l^2}\Big) }}{1-\frac{m^2}{l^2}}$

A régi KöMaL számokat nézegetve rátaláltam feladatodnak a Te megszövegezésed szerinti kitűzésére is. Gy. 914.:

http://db.komal.hu/scan/1964/04/96404173.g4

A megoldás pedig itt:

http://db.komal.hu/scan/1965/04/96504153.g4

Tetszik a válaszod. Részben hasonló cipőben járok: 73 éves vagyok, így az 1965-ös számokat én is olvastam régen, de az élet úgy hozta, hogy inkább számítástechnikából élek, semmint matematikából. Szabadidőmben újra örömömet lelem matematikai feladatok megoldásában (ezeket részben magamnak találom ki, részben innen-onnan gyűjtöm).

RE: Áruld el, hogyan találtál rá erre a megoldásra?

A Ludas Matyi vicclapnak volt egy mottója: "Nincsenek régi viccek, csak öreg emberek. Egy újszülöttnek minden vicc új."

Ha az ember elég öreg ahhoz, hogy már az 1965-ös KöMaL-okat is olvasta, de még elég fiatal ahhoz, hogy ne felejtsen el mindet, egy-egy feladat kapcsán beugrik, hol látott valami hasonlót.

Áruld el, hogyan találtál rá erre a megoldásra?

Elmondom az én megoldásomat, amely ugyan számoláson alapul, de talán a szerkesztés egyszerűbb.

Induljunk ki a kész ábrából:

Legyen $\displaystyle BC$ az adott oldal, $\displaystyle AM$ az adott magasság és $\displaystyle AF_1$ az adott szögfelező.

Megrajzoltuk még az $\displaystyle AF_1$-re merőleges $\displaystyle AF_2$ külső szögfelezőt is.

Az $\displaystyle AMF_1\triangle$ nyilván könnyen szerkeszthető és az $\displaystyle F_2$ pont is könnyen kitűzhető.

Ha ismernénk a $\displaystyle BF_1$ szakasz $\displaystyle x$ hosszát, akkor készen lennénk.

Legyen a $\displaystyle BC$ oldal hossza $\displaystyle a$, az $\displaystyle F_2F_1$ távolság pedig $\displaystyle d$!

Írjuk fel a szögfelező tétel alapján a következő összefüggést:

$\displaystyle \frac{x}{a-x}= \frac{d-x}{d+a-x}$

A kapott másodfokú egyenlet megoldása (csak az érdekel, amelyik kisebb $\displaystyle a$-nál):

$\displaystyle x= \frac{a+d-\sqrt{a^2 + d^2}}{2}$

$\displaystyle \sqrt{a^2 + d^2}$ egy olyan derékszögű háromszög átfogójának a hossza, amelynek befogói $\displaystyle a$ és $\displaystyle d$ hosszúságúak.

Nézzük ezek után a szerkesztést! Szerkesszük meg az $\displaystyle AMF_1$ háromszöget és tűzzük ki az $\displaystyle F_2$ pontot! Az $\displaystyle F_1F_2$ egyenesre mérjük fel az $\displaystyle a$ szakaszt $\displaystyle F_1$-ből az $\displaystyle F_2$-vel ellentétes oldalon. A kitűzött pont $\displaystyle P_1$ és az $\displaystyle F_2P_1$ szakasz hossza $\displaystyle a+d$.

Állítsunk merőlegest az $\displaystyle F_1F_2$ egyenesre az $\displaystyle F_1$ pontban és mérjük fel rá az $\displaystyle a$ szakaszt! A kitűzött pont $\displaystyle P_2$. Az $\displaystyle F_2P_2$ távolság nyilván $\displaystyle \sqrt{a^2 + d^2}$.

Mérjük rá az $\displaystyle F_2P_2$ távolságot az $\displaystyle F_2P_1$ szakaszra $\displaystyle F_2$-ből indulva. Az így kapott pont $\displaystyle P_3$. Nyilván a $\displaystyle P_1P_3$ szakasz hossza $\displaystyle a+d-\sqrt{a^2 + d^2}$. A szakasz felezőpontja legyen $\displaystyle K$!

A $\displaystyle KP_1$ szakasz hossza $\displaystyle x$, tehát $\displaystyle K=C$, azaz megkaptuk a háromszög másik csúcsát. A harmadik csúcs kitűzése most már nem jelent problémát és a szerkesztést befejezettnek tekinthetjük.

Röviden a diszkusszió: ha az adott magasság és az adott szögfelező egyenlő hosszú, akkor egyenlőszárú háromszögről van szó, amelynek szerkesztése nem okozhat problémát, ha pedig a szögfelező hosszabb a magasságnál, akkor a szerkesztés mindig elvégezhető.

Az $\displaystyle f_c$ és $\displaystyle m_c$ által bezárt szög $\displaystyle \frac{\alpha - \beta}2$ Így a feladatot visszavezettük erre:

Szerkesszünk háromszöget ha adott egy oldala, az oldalhoz tartozó magasság és az oldalon fekvő két szög különbsége.

Ez volt az 1964. évi Arany Dániel verseny egyik feladata, megoldása a KöMaL 1965. évi 1. számának 2. oldalán olvasható.

Szerkesszünk háromszöget, ha adott egy oldala, az oldalhoz tartozó magasság és a szemközti csúcsból induló szögfelezőnek a háromszögbe eső darabja!