Fórum: Versenyfeladatok

Szeretnél hozzászólni? Jelentkezz be.

[123] Loiscenter	2014-01-16 12:15:16
Téhát nem elemi a bizonyitás. Esetleg ha valtoztatva az alakzatot haromszöggé (pédaul) akkor sem remélkedhetünk egy (vonalzos körzös) elemi megoldás? ( a két meröleges egyenes esetrol van némi remény - szerintem!!!)

[122] sakkmath	2014-01-16 11:31:46
Az 1889. feladatban megfogalmazott tétel bizonyítása REIMAN ISTVÁN: A GEOMETRIA ÉS HATÁRTERÜLETEI című könyve 15.5. fejezetében, a 297. oldalon olvasható (Gondolat Kiadó, 1986).
Előzmény: [120] Loiscenter, 2014-01-15 20:23:37

[121] Sirpi

2014-01-16 11:23:30

Az első (1888.) megoldásvázlata:

minden $\alpha$ szöghöz rendeljuk hozzá azt az (egyértelműen meghatározható) egyenest, ami felezi a területet és az x tengellyel $\alpha$ szöget zár be. Ha a szög végigmegy 0-tól 180 fokig, a definiált egyenesek folytonosan változnak. Legyen az f( $\alpha$ ) függvényünk az egyenes feletti kerületszakasz éz egyenes alatti kerületszakasz hosszának különbsége. f is folytonos és f(0)=-f( $\pi$ ). Tehát f valahol előjelet vált a [0, $\pi$ ] intervallumon (vagy tartósan 0, pl. középpontosan szimmetrikus alakzatoknál).

A nullhelyhez tartozó szöghöz rendelt egyenes pont a kívánt tulajdonságokkal fog rendelkezni.

Előzmény: [120] Loiscenter, 2014-01-15 20:23:37

[120] Loiscenter

2014-01-15 20:23:37

HELP: A RÓKA SÁNDOR : 2000 feladat az elemi matematika köébol:

1888. Mutassuk meg, hogy egy korlátos, konvex alakzathoz mindig található egyenes, mely felezi annak kerületét és területét is

1889. Mutassuk meg, hogy egy korlátos sikidomot szét lehet vágni két egymásra meröleges vágással négy egyenlö területü részre.

mind két feladatnak nem találhatók megoldásai

[119] Loiscenter	2014-01-07 12:10:09
köszönöm Erben Péter !
Előzmény: [118] Erben Péter, 2014-01-07 10:42:55

[118] Erben Péter

2014-01-07 10:42:55

Itt van néhány megoldás: Egyptian fraction representations of 1 with odd denominators

Nem nehéz mohó algoritmust használó programot írni a felbontásra. Az viszont máig eldöntetlen (ha jól tudom), hogy a "páratlan mohó felbontás algoritmus" minden tört esetén befejeződik-e véges sok lépésben: Odd greedy expansion

Előzmény: [117] Loiscenter, 2014-01-07 10:11:18

[117] Loiscenter	2014-01-07 10:11:18
Help - Szeretném tudni megoldást arra : különbözö páratlan pozitiv számok reciprokával elöállitani 1 -et!
Előzmény: [96] Sirpi, 2009-04-21 15:03:32

[116] nadorp	2013-04-18 08:24:52
A 7. feladat tetszett, mármint a "meglepő" végeredmény.
Előzmény: [115] jonas, 2013-04-16 18:49:04

[115] jonas

2013-04-16 18:49:04

A 2013. évi BME Matematika versenyt 2013. április 15-n rendezték meg.

1. Adott a síkon 4 pont úgy, hogy egy láthatatlan négyzet minden oldalán pontosan egy fekszik belőle. Szerkesszünk egy ilyen tulajdonságú négyzetet. Mikor egyértelmű a megoldás?

2. Adott 12 szám az (1, 12) intervallumon. Lássuk be, hogy kiválasztható közülük 3 úgy, hogy az a háromszög, melynek oldalhosszai ezen értékek, hegyesszögű. Igaz marad-e az állítás, ha a számokat az [1, 12] zárt szakaszból választjuk?

3. Egy gráf „majdnem síkbarajzolható”, ha lerajzolható úgy a síkra, hogy minden élét legföljebb egyetlen másik él metszi. Legyen e_m(n) az a maximális érték, amely élszámmal még létezik n csúcsú majdnem síkbarajzolható egyszerű gráf. Adjunk meg minél jobb c,c^* értékeket, amelyre $\exists$ K úgy, hogy cn-K $\le$ e_m(n) $\le$ c^*n+K minden „elég nagy” n-re.

4. Legyenek v₀,...v_n $\in$ Rⁿ egy $\Delta$ $\subset$ Rⁿ szimplex csúcsai. $\Delta$ duálisa az a $\Delta$ ^d szimplex, amelynek csúcsai a $w_j = \frac{1}{n} \sum_{k\ne j} v_k$ (j=0..n) pontok. Bizonyítsuk be, hogy ha K $\subset$ Rⁿ kompakt, konvex és nem üres belsejű, akkor létezik olyan $\Delta$ szimplex, hogy $\Delta$ $\supset$ K $\supset$ $\Delta$ ^d.

5. Legyen X egy olyan mátrix, amelynek minden elemének abszolút értéke legföljebb 1. Adjunk minél jobb – ha lehet, optimális – fölső becslést |det(X)|-re a következő két esetben: a) X 3×3-as valós, b) X n×n-es komplex.

6. Legyen S $\subset$ R egy pozitív Lebesgue-mértékű halmaz. Bizonyítsuk be a kontinuum-hipotézis feltételezése nélkül, hogy S kontinuum számosságú.

7. Milyen a₀ $\in$ C esetén lesz konvergens az a_k=2ka_k-1-1 (k=1,2,...) rekurziós relációval megadott sorozat, és mi ilyenkor a határérték?

8. Az f:T $\to$ C folytonos, korlátos függvény a T={z $\in$ C:0 $\le$ Im(z) $\le$ 1} tartomány belsejében holomorf. Legyen $N(x) = {\rm sup}_{y \in {\bf R}} |f(x + iy)|$ . Bizonyítsuk be, hogy a) N(x) $\le$ max{N(0),N(1)} és b) N(x) $\le$ N(0)^1-xN(1)^x minden x $\in$ [0,1]-re.

9. Mutassuk meg, hogy egy pozitív szemidefinit mátrix pozitív szemidefinit gyöke egyértelmű (azaz ha X,Y $\ge$ 0, akkor X²=Y² és X=Y ekvivalens), és ezt kihasználva (vagy bárhogy máshogy) bizonyítsuk be, hogy az A, B pozitív definit mátrixok geometriai közepe

$A \# B = A^{\frac{1}{2}} (A^{-\frac{1}{2}} B A^{-\frac{1}{2}})^{\frac{1}{2}} A^{\frac{1}{2}}$

független a sorrendtől: A#B=B#A.

10. Legyen X egy binomiális eloszlású valószínűségi változó n és p=1/2 paraméterkkel, Z egy standard normális eloszlású változó és $Y = \frac{1}{\sqrt{n}}(2X - n)$ . Mutassuk meg, hogy ${\bf E}(e^{tZ}) = e^{\frac{1}{2}t^2}$ és ezt kihasználva (vagy bárhogy máshogy) bizonyítsuk be, hogy ${\bf E}(e^{tY^2}) = {\bf E}(({\rm cosh}(\sqrt{\frac{2t}{n}}Z))^n)$ minden t>0 és n=1,2,.. értékekre.

Előzmény: [104] jonas, 2011-05-04 13:24:56

[114] w

2013-01-13 21:50:02

2012-es versenyfeladat nyomán:

Egy dobozban 2012 fehér golyónk van és még feleslegben piros és zöld golyó a dobozon kívül. Cserélgetjük a golyókat, ezt a következő módon tehetjük:

(1.) két zöldet két fehérre és fordítva,

(2.) három pirosat és egy fehéret egy zöldre,

(3.) egy zöldet és két fehéret két pirosra,

(4.) öt zöldet két pirosra és két fehérre, vagy végül

(5.) egy pirosat és egy zöldet egy fehérre cserélünk.

a) Elérhető-e, hogy három golyó maradjon?

b) Mutassuk meg, hogy ez a három golyó háromféle színű!

[113] w	2013-01-13 20:52:39
A nyolcadik feladat nyolcadikos példa. Megoldás: Vonjuk össze a törteket, ekkor a nevező páros (ha n>1), a számlálóban pedig pontosan egy páratlan tag van (2^[log₂n] bővítettje), a számláló páratlan, és ez maga után vonja, hogy nem lehet a tört egész.
Előzmény: [108] jonas, 2012-04-27 01:00:54

[112] Lóczi Lajos	2012-11-28 21:17:35
A lineáris feltételekből kifejezed pl. a-t és b-t c-vel, és ezeket behelyettesíted a négyzetes kifejezésbe. A végeredmény plusz kettő egyenlő azzal a számmal, ahányféle szabályos konvex politóp létezik öt- és magasabb dimenzióban.
Előzmény: [111] w, 2012-11-28 19:19:11

[111] w	2012-11-28 19:19:11
Érdekelne ennek a 9. osztályos versenyfeladatnak a megoldása: "Számítsuk ki az aa-bb+c*c kifejezés értékét, ha tudjuk, hogy a-7b+8c=4 és 8a+4b-c=7."

[110] Szabó Máté	2012-05-07 13:31:15
Az első két feladat szándékosan könnyebb, azokra csak az elsőévesek adhattak be megoldást.
Előzmény: [107] Róbert Gida, 2012-04-26 23:38:58

[108] jonas	2012-04-27 01:00:54
A nyolcadik ki van mondva a Konkrét Matematikában is.
Előzmény: [107] Róbert Gida, 2012-04-26 23:38:58

[107] Róbert Gida

2012-04-26 23:38:58

Vannak benne halálismert példák. Mondjuk ilyen az első: http://mathworld.wolfram.com/FrobeniusNumber.html.

A nyolcadiknak általánosítását még Kürschák látta be: http://mathworld.wolfram.com/HarmonicNumber.html.

Előzmény: [106] jonas, 2012-04-26 23:14:57

[106] jonas

2012-04-26 23:14:57

Az idei BME Matematika verseny feladatai már elérhetők ugyanonnan. Ez a verseny a BME mindenféle szakos hallgatóinak szól, elsősorban elsőtől negyedévig, és idén valóban a nyolcból öt karról jöttek versenyzők. A verseny 2012. április 17-n volt.

Bemásolom ide is a feladatokat.

1. Legyenek a és b relatív prím természetes számok. Melyik az a legnagyobb természetes szám, amely nem áll elő ak₁+bk₂ alakban, ahol k₁,k₂ nemnegatív egészek?

2. Legyen f:R $\to$ R folytonos függvény, melyre $\lim_{x\to\infty} \int_0^x f = A$ véges határérték. Mutassuk meg, hogy bármely $\delta$ >0 mellet az $\int_0^\infty e^{-\delta t} f(t) dt$ improprius integrál konvergens és

$\lim_{\delta \to 0+} \int_0^\infty e^{-\delta t} f(t) dt = A.$

3. Legyen T₁(x) az e^x függvény a pontbeli érintőegyenese. Melyik a értékre lesz max_[0,1]|e^x-T₁(x)| a legkisebb?

4. Egy tetraéder AB és CD élei merőlegesek egymásra, mindegyik 2a hosszú. A felezőpontjaikat összekötő EF szakasz mindkét élre merőleges, az AC, AD, BC, BD éleknél lévő lapszögek 60°-osak. Meghatározandó a tetraéder beírt és körülírt gömbjeinek sugara.

5. Keressük meg az összes olyan f,g:R $\to$ R folytonosan differenciálható függvénypárt, melyre f²+g²=1 és f'²+g'²=1.

6. Adott egy n szögpontú egyszerű gráf. Bizonyítsuk be, hogy

a. Ha minden pont foka legalább 3, akkor van a gráfban páros hosszú kör.

b. Abból, hogy minden pont foka legalább (n-1)/2, nem következik, hogy van a gráfban páratlan kör. Adjunk ellenpéldát minden n-re.

c. Ha minden pont foka legalább (n+1)/2, akkor van a gráfban páratlan kör.

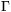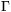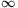7. Az x $\ge$ 0 félsíkban tekintsünk K_n köröket, melyek az origóban érintik az y tengelyt, és K_n sugara kétszerese K_n+1 sugarának, n=1,2,.... Adott jelre a K_n+1 körök azonos konstans szögsebességgel gördülni kezdenek a K_n körvonalon, azt belülről érintve, negatív forgásirányban. A K_n kör középpontja által leírt görbe legyen $\Gamma$ _n. Mi lesz $\Gamma$ _n határgörbéje, ha n $\to$ $\infty$ ? Adjuk meg a határgörbe paraméterezését.

8. A $\sum_{k=1}^n \frac{1}{k}$ összeg milyen n esetén egész szám?

9. Legyen f:R $\to$ R akárhányszor differenciálható és tegyük fel, hogy az $S(x) = \sum_{n=0}^{\infty} f^{(n)}(x)$ függvénysor lokálisan egyenletesen konvergens. Adjuk meg az S(x) összegfüggvényt zárt alakban.

10. Legyenek f,g:R³ $\to$ R⁵ lineáris leképzések. Bizonyítsuk be, hogy vannak olyan R³=V₁(+)V₂, R⁵=W₁(+)W₂ direkt összeg-felbontások, hogy i=1,2-re f(V_i) $\subset$ W_i, g(V_i) $\subset$ W_i és V_i(+)W_i $\ne$ 0.

11. Sorban állok a postán. n ablaknál szolgálják ki az ügyfeleket. Egyetlen sor van, ahonnan az éppen felszabaduló ablakhoz megy, aki következik. Egy ügyfél kiszolgálási ideje bármelyik ablaknál független, $\lambda$ >0 paraméterű exponenciális eloszlást követ. Mi a valószínűsége annak, hogy a k-ik ugánam következő előbb végez, mint én? Mi a válasz akkor, ha az i-ik ablaknál a kiszolgálási idő eloszlása $\lambda$ _i>0 paraméterű exponenciális eloszlás?

[105] jonas	2011-05-04 13:54:27
Azt elfelejtettem hozzátenni, hogy itt vannak a BME Matematika Verseny korábbi feladatsorai.

[104] jonas

2011-05-04 13:24:56

Alább következnek a 2011. évi BME Matematika Verseny feladatai.

A verseny beülős, 2011. április 14-én zajlott, a munkaidő 4 óra. Bármely BME hallgató részt vehet, bármilyen szakról és évfolyamról. Az első feladat csak az elsőéves hallgatóké, a többi feladat mindenkinek szól.

1. Adott a,b,c,d oldalhosszúságú síkbeli négyszögek közül melyik lesz maximális területű? Az oldalak ebben a sorrendben csatlakoznak.

2. Melyek azok a tízes számrendszerben felírt természetes számok, melyek utolsó számjegyét az elejére áthelyezve az eredeti szám 2/3-át kapjuk?

3. Legyen A invertálható n×n-es mátrix. Tegyük fel, hogy az A és A^-1 mátrixok minden eleme nemnegatív. Bizonyítsuk be, hogy van olyan k>0 egész, hogy A^k diagonális mátrix.

$\int_{0}^{\infty} e^{-(y^2+y^{-2})}dy = ?$

5. a. Legyenek v₁,...,v_n egységvektorok egy euklideszi térben, |<v_i,v_j>|<1/(n-1), ha i $\ne$ j. Mutassuk meg, hogy v₁,...,v_n lineárisan függetlenek.

b. Lengyen m=(n-1)n/2+1, v₁,...,v_m egységvektorok, |<v_i,v_j>|²<1/(m-1), ha i $\ne$ j. Mutassuk meg, hogy v₁,...,v_m közül kiválasztható n lineárisan független vektor.

6. Az irányított G egyszerű gráf irányított kromatikus száma, $\chi$ _i(G) az a legkisebb k, amelyre k színnel színezhetők a csúcsok úgy, hogy egy él két vége különböző színű és bármely adott színpárban csak az egyik irányba vezethet él. Mutassuk meg, hogy nincs olyan f:N $\to$ N függvény, melyre $\chi$ _i(G) $\le$ f( $\chi$ (G)) teljesül minden G-re, ahol $\chi$ (G) a megfelelő irányítatlan gráf kromatikus száma. Azaz az irányított kromatikus szám nem becsülhető a kromatikus szám ismeretében.

7. Mutassuk meg, hogy ha f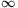 $\in$ C(0, $\infty$ ) és minden x>0-ra $\lim_{n\to\infty} f(x/n) = 0$ , akkor $\lim_{x \to 0+} f(x) = 0$ .

8. Legyen 1 $\le$ k $\le$ n. Mutassuk meg, hogy az 1,2,...,n számok egy véletlen permutációjánál

a. 1/k valószínűséggel lesznek az 1,2,...,k számok ugyanabban a ciklusban,

b. 1/k! valószínűséggel lesznek az 1,2,...,k számok csupa különböző ciklusban.

9. Legyenek P,Q ortogonális projekciók egy véges dimenziós térben. Mutassuk meg, hogy

Tre^P+Q $\le$ Tr(e^Pe^Q).

10. Legyen f(z) reguláris a Rez>0 félsíkon. Tegyük fel, hogy

$\lim_{z\to0, {\rm Re} z>0} \frac{f(z) - a_0}{z} = a_1.$

Bizonyítsuk be, hogy tetszőleges $\delta$ >0 esetén

$\lim_{z\to0, {\rm Re} z>\delta|{\rm Im} z|} f'(z) = a_1.$

Feladatsor vége.

A továbbiak az én megjegyzéseim.

A 6. feladatot értsük úgy, hogy csak olyan G gráfokat tekintünk, amelyekben semelyik két csúcs között nincs oda-vissza él (így az irányított kromatikus szám mindig véges).

A 8. feladatra keressetek olyan megoldást, ami az a. és b. részt is megoldja, de olyan megoldást is, ami csak az a. részt oldja meg.

[103] lorantfy	2009-06-20 21:19:21
Köszönöm!
Előzmény: [101] Tassy Gergely, 2009-05-03 16:33:01

[102] sakkmath	2009-05-04 10:01:47
Köszönöm, egyetértek :-)
Előzmény: [100] jenei.attila, 2009-05-02 22:45:46

[101] Tassy Gergely	2009-05-03 16:33:01
Az idei Kalmár első fordulóján tűzték ki, 6. osztályban...
Előzmény: [99] lorantfy, 2009-04-24 12:49:58

[100] jenei.attila	2009-05-02 22:45:46
a válasz: 9
Előzmény: [86] sakkmath, 2009-04-17 17:25:21

[99] lorantfy	2009-04-24 12:49:58
Köszönöm a megoldásokat! Valóban kitűzték általános iskolai versenyen. Egy szegedi kolléga mesélte nekem, hogy a tanítványa próbálgatással megoldotta. (Sajnos nem emlékszem, melyik versenyen). Talán Káli gúla (89) megoldására gondoltak a rendezők? Olyan számnál, amelyik előállítható osztópárjai összegeként, talán könnyebb lett volna, pl. 30 esetén. Szerintem ilyesmire gondolt rizsesz (93)-ban.

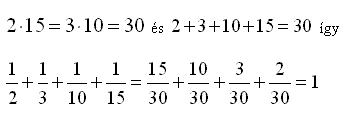Előzmény: [89] Káli gúla, 2009-04-20 12:07:43

[98] Káli gúla

2009-04-21 16:34:16

Az a bizonyos 13 szám: A028229: 2, 3, 5, 6, 7, 8, 12, 13, 14, 15, 19, 21, 23. Egy vázlatos bizonyítás olvasható itt: http://perplexus.info/show.php?pid=2798&op=sol .

Az egyiptomi törtekről nagyon sok mindent lehet megtudni ezen az oldalon: "www.ics.uci.edu/~eppstein/numth/egypt". Egészen különleges olvasmány J. Baez előadása http://math.ucr.edu/home/baez/week182.html.

Előzmény: [96] Sirpi, 2009-04-21 15:03:32

[1] [2] [3] [4] [5]

Már regisztráltál?
Új vendég vagy?