Fórum: Héttusa feladatok

Mivel az önleltározó hétjegyű szám számjegyei kicsikék kell hogy legyenek, MI nélkül is lesz feltételeknek megfelelő számunk. Arra jó, hogy ha embernek már van kettő száma, akkor nem nagyon keresgél tovább, hanem nézi a Héttusa következő feladatát.

Héttusa, 52. feladat

A héttusában nem egészen sportszerű módon a mesterséges intelligenciát hívtam segítségül. A feladat megadása után azt kértem, hogy írjon egy olyan programot, amely megvizsgálja az összes hétjegyű számot, és megadja, hogy melyek az önleltározók.
A ChatGPT rögtön megértette a feladatot, és közölte a két számot (3022003, 3103003).
A kínai DeepSeek-nek és Elon Musk Grok-3-jának ez nem sikerült.

56. feladat módosítása. Ezen is lehet elmélkedni. Nem kiválasztjuk a 7x7-es táblázat 15 celláját, hanem kilyukasztjuk ugyanazzal a feltétellel. Semelyik két cellának nincs közös csúcsa vagy nincs közös oldala. A táblázat szimmetriáival egymásba vihető tizenötösök ugyanazt a táblázatot jelentik. (Lyukas négyzetek.)

55. feladat Megjegyzés:  Egy hosszabb, de talán átláthatóbb módszer, ha az első (17 főnek a fizetését megduplázza, és a többiek nem kapnak fizetést) javaslat után a kancellár 15-ször azt javasolja, hogy az egyik 2 talléros nem kap fizetést és ezt átadja(szétosztja) (1+1) a két "kedvenc" emberének... Így további 15 lépésben két kézben (17+17) összpontosul a vagyon. Ezt (illetve hárommal kevesebbet) meg három (0-s) ember lefizetésével megszerezheti..

Megjelent a Héttusa új fordulója: $\displaystyle \rightarrow$ 8. forduló

A beküldési határidő: április 7.

Az előző, a 7. forduló megoldásai itt olvashatók.

Héttusa 7. forduló (2024. december), 49. feladat→

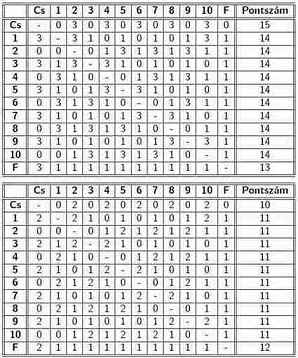
Ez a feladat olyan nehéz volt, hogy csak keveseknek sikerült megoldaniuk. Én sem boldogultam vele. A megoldás leírása alapján elkészítettem az eredménytáblázatokat.

A Csodacsapat (Cs) és a Falábúak (F) mellett még 10 csapat játszik, őket jelöljük az 1, 2, . . . , 10 számokkal.

Az új (3-1-0-ás) és a régi (2-1-0-ás) pontszámítás szerinti eredménytáblázatok:

Megjelent a Héttusa új fordulója: $\displaystyle \rightarrow$ 7. forduló

A beküldési határidő: január 12.

Hogyan lehetne játékossá, népszerűvé tenni a feladatmegoldást?

Írtam erről, egy lehetőségről, egy matekos párbajról: $\displaystyle \rightarrow$ Párbajozzunk a matematikaórán?

20. kerdes a 37. feladat alapján -

a mutassuk meg, hogy tetszoleges $\displaystyle \varepsilon>0$-ra es minden eleg nagy $\displaystyle n$-re letezik tablazat, amiben a legnagyobb elem legfeljebb $\displaystyle (1+\varepsilon) n^2 \ln n$ (ez persze explicit egyenlotlensegge teheto valamifele $\displaystyle n^2 \ln n+f(n)$ formaban ahol $\displaystyle f(n)=o(n^2\ln n)$). Van-e erosebb felso becslesunk?

Héttusa 39. feladata. A nyomozó 6 nap alatt biztosan megtalálja a bűnöst. Az ilyen típusú feladatoknál szoktam olyanra is gondolni, attól függetlenül, hogy kiolvasható-e a szövegből vagy nem, az, hogy kell-e ilyenre gondolnunk, hogy mondjuk 5 nap adataiból egy nálam sokkal többet látó valaki, már tudja a bűnöst. Mindketten ugyanazt nézzük, de van, aki nálam sokkal többet lát. /Talán kicsi a valószínűsége./

Nagyon tanulságos a 31. feladat (labdarúgó-bajnokság). Milyen könnyen lehet elsőből utolsó!

Ha jól számolom a 19. kérdés következik és nekem ez pont a 19. feladat általánosított átfogalmazása: A kör kerületén felvett n db pont legfeljebb hány hegyesszögű háromszöget határoz meg?

Jav.: Tehát az új  győztesnek legalább 4 győzelme volt.

Addig akkor megvan, hogy a régi győztes mérlege pozitív (több győzelem, mint vereség), az új győztesé negatív.

Legyen a két csapatnak $\displaystyle \omega, \omega'$ győzelme és $\displaystyle \delta, \delta'$ döntetlene. Ha a vessző nélküli számok tartoznak az új bajnokhoz, akkor a helycsere feltétele:

$\displaystyle 2(\omega-\omega')+\delta-\delta' < 0 < 3(\omega-\omega')+\delta-\delta' ,$

amiből átrendezéssel azonnal adódik, hogy $\displaystyle \omega>\omega'$, sőt a

$\displaystyle 2(\omega-\omega')<\delta'-\delta< 3(\omega-\omega')$

szigorú egyenlőtlenség miatt $\displaystyle \omega-\omega'\ge2$ és így $\displaystyle \delta'-\delta\ge5$, méghozzá $\displaystyle \omega-\omega'=2$ esetén $\displaystyle \delta'-\delta=5$.

Ha $\displaystyle \omega=3$, akkor $\displaystyle \omega'\ge1$ miatt csak $\displaystyle \omega'=1$ lehet, így a régi győztes mérkőzéseinek száma pontosan $\displaystyle 1+(\delta+5)+0$, az új győztesé viszont legalább $\displaystyle 3+\delta+4$ lenne, ami lehetetlen. Tehát a régi győztesnek legalább 4 győzelme volt.

A feladatban az volt, hogy legalább 7 csapat indul. Meg lehet valósítani 10 csapattal. A 1 gy, 8 d, 0 v B-I 1 gy, 7 d, 1 v J 4 gy, 0 d, 5 v Én csak azt használtam, amit a feladatban leírtak. Más dolgok felhasználása csak kiegészítheti az alapfeladatot, szerintem. Különböző országokban különbözőféleképpen döntik el pontegyenlőség esetén, hogy a bajnokságokon ki a győztes.

31. feladat alternatív megoldása, csak azért nem tetszik nekem, mert gólarányokról a feladatban nem volt szó, bár lehet hogy ez mindenkinek egyértelmű (nekem nem, de igaz én eddig azt se tudtam hogy 3 pontot kap a győztes, nem követem a sportot) Én az alábbi megoldást adtam:

Lehetséges (Régi pontozás szerint minden meccsen két pontot osztanak ki ezért az átlagos végső pontszám csapatonként = résztvevőkszáma-1. A vesztesnek ennél kevesebbet kell kapnia (és ekkor értelemszerűen lesz legalább egy csapat aki ennél többet kapott) Így a győztesnek legalább két ponttal volt több. Ha régi pontozásról áttérünk újra akkor mindenki a meglevő pontszámához kap még annyi pontot ahány győzelme volt. Hogy a "régi vesztes" új győztes legyen akkor legalább 3 ponttal kell többet kapnia (mert 2 pont különbség biztos volt köztük) mint a régi győztes (és a győztesnek kell lennie legalább egy nyert meccsnek), tehát ha a régi vesztesnek 4 győzelme és 5 veresége volt, a nyertesnek 1 győzelme és 8 döntetlen, mindenki másnak 1 győzelem, 7 döntetlen és 1 vereség akkor az megfelelő. Ez előállhat úgy hogy A (ő a régi nyertes) megveri B-t mindenki mással döntetlent játszik. A többi meccsek 4 db hármas körbeverése (x legyőzi y-t, y legyőzi z-t,z legyőzi x-t) úgyhogy B szerepel mindegyik hármasban. Minden más meccs döntetlen. A fentiekből következik, hogy ha a régi vesztesnek legalább 4 győzelemmel kell rendelkeznie (és így van az átlag alatt), akkor az átlag pontszám régen legalább 9, a résztvevők száma legalább 10.

A mostani pontozás szerint viszont az A az első (a pontszáma révén):

Az A csapat a régi pontozás szerint az utolsó (a gólaránya miatt):

A Héttusa 31. feladatának egy alternatív megoldása:

31. Egy labdarúgó-bajnokságon legalább 7 csapat indul, és bármely két csapat pontosan egy mérkőzést játszik egymással. Lehetséges-e, hogy a bajnokság győztese a régi pontozási rendszer szerint az utolsó helyen végezne?
A mostani pontozás szerint a mérkőzés győztese 3 pontot, a vesztes 0 pontot kap, döntetlen esetén pedig 1-1 pontot kap a két csapat. A régi rendszer abban különbözik a jelenlegitől, hogy a győzelemért 3 pont helyett 2 pont jár.

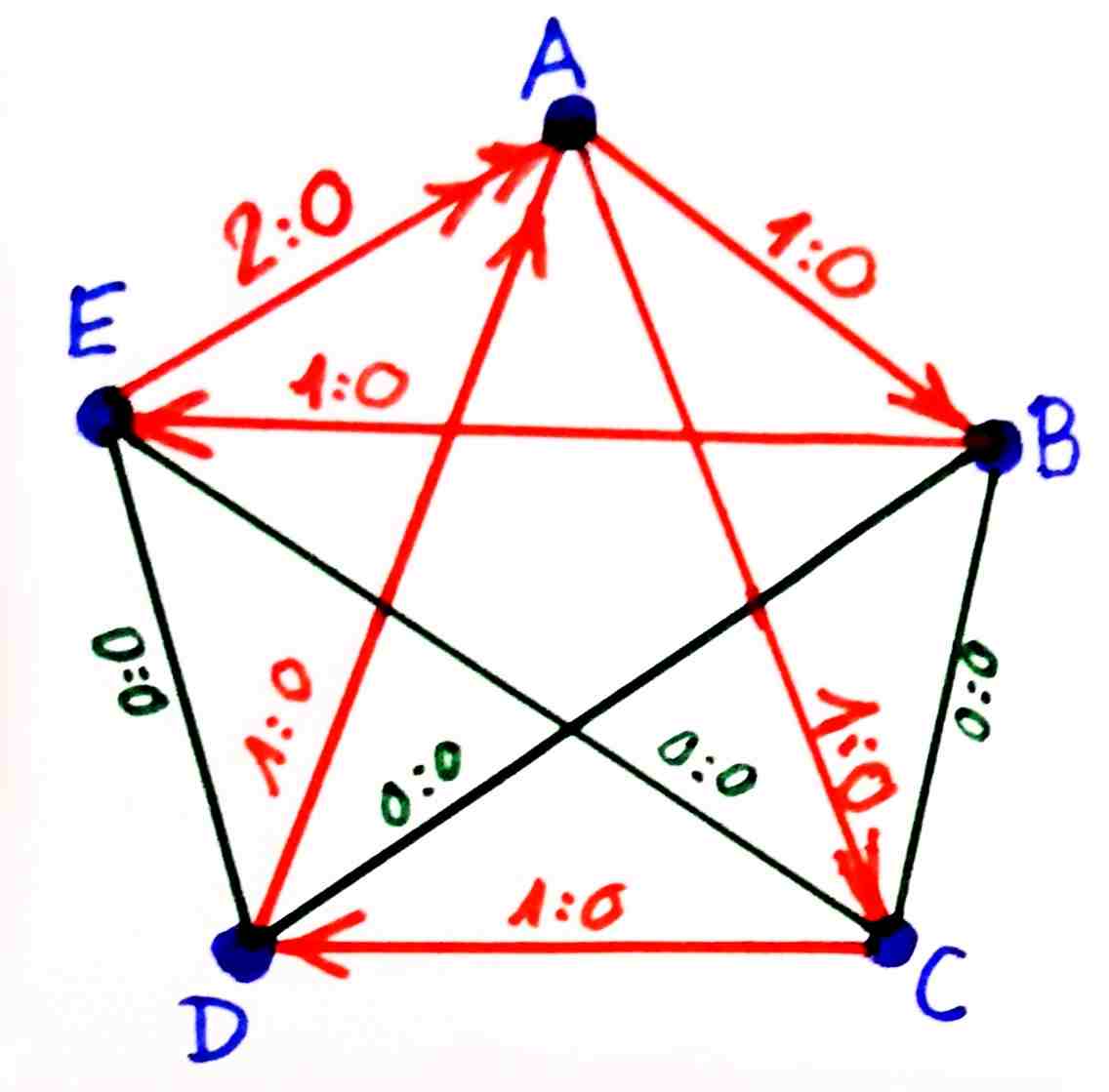
Ez lehetséges minden olyan bajnokságban, ahol az induló csapatok száma legalább 5.
Például 5 csapat indulása és a lehető legkevesebb gól esetén (ha további 6., 7., 8. . . csapat indul, és azoknak az összes mérkőzésük döntetlen, akkor is az A csapat az utolsó vagy az első, a régi vagy a mostani pontozás szerint):

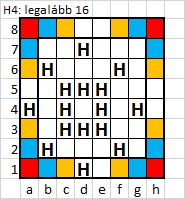
A 100-adik hozzászólás táblázatában a Huszárok 4 ütéssel rovatba egy "16 ?" bejegyzést eszközölhetünk a mellékelt ábra alapján. A színezések indoklása a K4-éhez hasonló. A tökéletes szimmetriához a 7×7-es sakktábla volna az igazi.

Megjelent a Héttusa új fordulója $\displaystyle \to$ 6. forduló

A beküldési határidő október 1.

Ezt követően itt is beszélgethetünk a feladatokról.

A 18. kérdéshez:

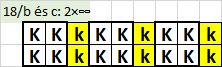
A 2×végtelen esetre példa az alábbi ábra. A sárgított királypárokban mindig csak 1-et meghagyva máris végtelen sok a lehetőség. Az így kapott 2-soros sávot szintén lehet fölfelé másolni, miáltal a fölső félsík vagy pl. a 8×végtelen sáv kitöltését is megkaphatjuk. (1 üres sort legalább hagyni kell a másolatok között.)

Máris van tehát végtelen sok példánk, az "összes" alapváltozatot talán Harold Scott MacDonald Coxeter tudta volna meghatározni...

A 18. kérdéshez:

A teljes síkot megcélozva a, z egyszínű mezőket fel is lehet fújni 2×2-es négyzetekké (változat 1), de ki is ritkíthatjuk (változat 2). Van egy 3. változat is, kétféle szemlélettel. Ez egy srégen vonuló minta, amelyet eltologatva újabb kitöltéseket kapunk. Bár e kitöltés szó talán nem pontos, hiszen véges sok sáv esetén elég ritkás a mintázat.

A 18. kérdéshez:

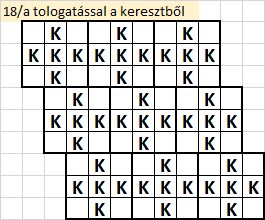
A keresztnek elnevezett király-csoportokat 3 soronként lehet jobbra vagy balra eltologatni - ami máris végtelen sok variációt jelent. Példa:

"A végtelen sakktábla viszont kitölthető például ..."

Mivel a minden irányban végtelen sakktáblán a csak sötét (csak világos) mezőkre rakott a királyok ugyanígy négy másikat ütnének, felmerül a következő

18. kérdés. Hány különböző elrendezés van a) a végtelen táblán, b) a felső félsíkon, c) egy $\displaystyle 8\times\infty$ sávban, amelyben mindegyik király pontosan négy másikat támad?

Királyok 4 ütéssel nem helyezhetők a sakktáblára!

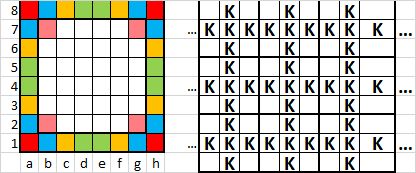
A sarkokba nem kerülhet király, hiszen csak 3 szomszédjuk van. b1-en álló királynak éppen 4 szomszédja marad, ezért a2-re is kerül király. Annak egyértelműen a3 és b3 szomszédjait kell elfoglalni újabb királyokkal. Csakhogy akkor b2K-t 6 kolléga fogná közre. Vagyis b1 és a2, meg elforgatottjaik szabadok! c1K-nak így pont 4 szomszédja van, ekkor c2K lefogja b3,c3,d3-at, ezáltal b2K-nak már nem lehet 4 király-ütője. Vagyis c1 kizárva, a tükörképeivel együtt. b2-nek ezért csak 3 szomszédja marad, vagyis nem lehet rajta király. d1-nek éppen 4 király-szomszédja volna, ekkor a d2K c3,d3,e3 kizárásával c2K-nak már nem lehet 4 szomszédja. Vagyis d1, e1 és tükörképeik is szabadok kell, legyenek. Ekkor tehát ott tartunk, hogy a tábla szélén nem lehet király. Vagyis a maradék 6×6-os táblára kellene tenni a királyokat. De ott sem lehet a sarkokba tenni - vagyis az elejétől ismételhetjük a gondolatmenetet. Így jutva a 4×4-es, majd 2×2-es tábláig, ahol már minden mező sarokmező. A végtelen sakktábla viszont kitölthető például az alábbi 5-királyos "kereszt"-ekkel:

A huszárok 3 ütéses elrendezésének inkább ezt őrizzük meg: