| [13] leni536 | 2010-07-01 04:32:38 |
 Fel kell osztani az áramkört kétkapukra és az átviteli mátrixot hatványozgatni komplexben. A hatványozásból az egyik sajátértékes tag el fog hanyagolódni a másikhoz képest, így fog kialakulni a végtelen létrára vonatkozó impedancia. Az érdekes, hogy megjelenik egy valós impedancia, ami valóban az, hogy terjed jobbra az energia, és mivel a létra végtelen, ez egy állandósult megoldást jelent.
Időbeli vizsgálatnál az áramkört leíró diffegyenletek stabilitását vizsgálnám a megoldások körül.
|
| Előzmény: [10] lgdt, 2010-02-06 00:04:25 |
|
| [12] HoA | 2010-06-17 12:26:34 |
 Fogalmazzunk inkább úgy, hogy milyen állapotban vannak a kapuk be- és kimenetei. A tároló stabil állapotában a tároló bemenetein 0 van, ami azt jelenti, hogy a kapuk egyik bemenete 0, a másik bemenete pedig a másik kapu kimeneti állapotától függ. Tehát mindkét kapu mindkét bemeneti állapota adott, megvan a "kapunként 2 jel" . Ha a tároló egyik bemenetének állapotát 1-re váltom, akkor továbbra is megvan a "kapunként 2 jel" . Lehet, hogy az egyik kapu kimeneti állapota megváltozik és ennek hatására a másik kapu bemenetéé is. De ekkor is megvan a "kapunként 2 jel" . És így tovább, amíg a tároló stabil állapota be nem áll. Tehát mindig megvan mindkét kapu mindkét bemeneti állapota.
|
| Előzmény: [11] Higgs, 2010-06-16 14:05:56 |
|
| [11] Higgs | 2010-06-16 14:05:56 |
 Sziasztok!
Először nem a kérdésemmel kezdem, hanem azzal amit értek. A NOR logikai kapunak ha 2 bemenete van, akkor 1-1 jel bemegy ezeken, majd 1 jel kijön a Boole-algebrának megfelelően. Az R-S tárolónál viszont az egyik kapun bemegy 1 jel majd a kijött jel bemegy a mésik kapu egyik bemenetén a másik bejövő jel melett, majd kijön 1 jel ami bemegy az előző kapu bemenetén. Remélem érthetően írtam. Ami nem világos, hogy ha bemegy 1-1 jel, akkor hogy jöhet ki bármelyiken is jel, ha ehhez kapuként 2 jel kell?
Előre is köszönök bármilyen segítséget!
|
|
| [10] lgdt | 2010-02-06 00:04:25 |
 Ha elfelejtem a komplex impedanciákat, és az időbeli viselkedést vizsgálom, akkor meg egy ilyen hullámegyenlet jön ki, és biztos tud olyat, hogy belemegy a hullám, és soha nem pattan vissza, így elvész az energia.
És ha tényleg ki is számolnám, és nem csak dumálnék róla, akkor lehet, hogy kijönne az impedancia is, és akkor lenne neki valós része.
|
| Előzmény: [8] lgdt, 2010-02-05 23:16:00 |
|
| [9] lgdt | 2010-02-05 23:27:28 |
 Úgy érted, egymenetes. Igen, először én is a háromszögszámokra találtam ki ezt a módszert, aztán a teljes megoldást csak hallottam, de annak semmi köze ehhez.
|
| Előzmény: [6] HoA, 2010-01-20 17:48:15 |
|
| [8] lgdt | 2010-02-05 23:16:00 |
 A végtelen hosszú kondenzátorlánc kapacitását én úgy értelmeztem, hogy az n hosszúságú kondenzátorláncok kapacitásaiból képzett sorozat határértéke. Ugyanez az új esetben nem működik, mert nemhogy nem konvergens a sorozat, de inkább kaotikus jelleget mutat.
Ha egy feszültséggenerátort kapcsolunk a végtelen lánc elejére, akkor a Kirchoff-törvényekből a felső csomópontok potenciáljaira egy differenciaegyenlet jön ki, de az első két potenciált tetszőlegesen megválasztva mindig van megoldása. Szóval nem értem ezt a végtelen LC-lánc dolgot. Hogy van ez?
Véges esetben egyébként természetesen mindig képzetes az impedancia.
|
| Előzmény: [5] leni536, 2010-01-13 22:49:14 |
|
| [7] jonas | 2010-01-20 17:55:47 |
 Szerintem igen, ha nem akarsz éles korlátot adni a menetek számára. Ugyanis először összeköthetsz alul n vezetéket, és fölül megtalálhatod, melyik n az (kivéve, ha n=1, amikor is inkább alul egy kivételével az összes többi vezetéket kötöd össze), utána erre az n vezetékre, aminek a halmazát már alul és fölül is ismered, alkalmazod a megoldásodat. Utána ugyanezt megcsinálod n másik vezetékkel úgy, hogy minden vezeték legalább egyszer sorra kerüljön.
|
| Előzmény: [6] HoA, 2010-01-20 17:48:15 |
|
|
| [5] leni536 | 2010-01-13 22:49:14 |
 Legyen hasonló a feladat, csak függőleges szakaszoknál kondik helyett legyenek L induktivitású tekercsek, a körfrekvencia pedig legyen  . Mekkora a komplex impedancia? Lehetséges-e, hogy az impedanciának lesz valós része? Ha igen, milyen következménnyel jár ez? . Mekkora a komplex impedancia? Lehetséges-e, hogy az impedanciának lesz valós része? Ha igen, milyen következménnyel jár ez?
|
| Előzmény: [3] lgdt, 2010-01-11 21:47:52 |
|
| [4] HoA | 2010-01-13 12:17:18 |
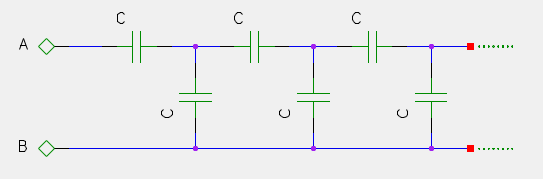
 Mivel a lánc végtelen, a kapacitása nem változik, ha az első két - az A-hoz ill. B-hez csatlakozó - kondenzátort leveszed róla. Tehát azt kell felírni, hogy az X kapacitású lánccal C -t párhuzamosan kapcsolva, majd ezzel C -t sorba kapcsolva az eredő kapacitás X lesz.
|
| Előzmény: [3] lgdt, 2010-01-11 21:47:52 |
|
| [3] lgdt | 2010-01-11 21:47:52 |
 3. feladat: Kapcsoljunk össze végtelen darab C kapacitású kondenzátort az ábrán látható módon. Mekkora az A és B pontok között mérhető kapacitás?
|
 |
|
| [2] lgdt | 2010-01-11 21:36:41 |
 Egyszer egy villanyszerelőt egy nagyon magas házba küldtek az elektromosságot bekötni. A földszinttől a 42. emeletig n db. egymástól elszigetelt drót vezetett. Mivel nem volt a drótokon jelölés, a bekötéshez meg kellett állapítani, melyik lenti vég melyik fenti véghez tartozik.
A megállapítás menete: a villanyszerelő lent összeköt drótokat tetszőlegesen (akár többet is egymással), majd felsétál a 42.-re (mert a lift áram nélkül nem működik), ott megméri, melyek vannak összekötve, ennek tudatában megint összeköt pár drótot fent, aztán lemegy a földszintre, szétbontja a vezetékeket és újból mér.
Érthető, hogy ezt nem szerette volna sokszor megismételni, ezért megkért minket, hogy segítsünk.
1. feladat: Írjunk olyan programot, amely megmondja, hogy n függvényében minimum hány fel- és lelépcsőzés szükséges az összes drót felcímkézéséhez (egy fel- és lemászás az 1-nek számít). Ha nem megoldható a probléma (pl. n=2 esetén), akkor jelezze.
2. feladat: Adjunk módszert az összekötéshez és a méréshez.
|
|
| [1] ati88 | 2007-03-13 20:19:05 |
 Üdv!
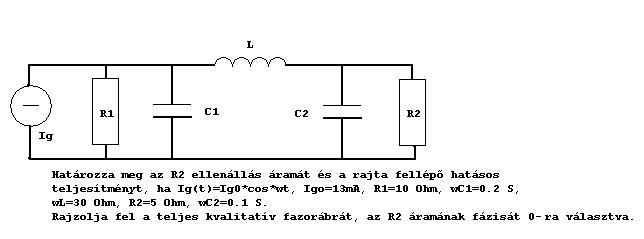
Adott az alábbi címen elérhető feladat:
Jövőhéten ZH-zok és jó lenne ha tudnám értelmezni a feladatot illetve ismerném annak megoldás-menetét. Sajnos, a helyzet eléggé kilátástalan, nem csak részemről :)
Köszönöm a segítséget!
|
 |
|
