Fórum: Lejárt határidejű Kömal fizika feladatok

Szeretnél hozzászólni? Jelentkezz be.

[15] csillagász	2012-06-06 17:52:11
Te hogyan mérnéd meg?
Előzmény: [14] Róbert Gida, 2012-06-05 23:07:04

[14] Róbert Gida

2012-06-05 23:07:04

M.324. Mérjük meg a Föld-Nap távolságot június 6-án a Vénusz Nap előtti átvonulásakor.

Mennyivel érdekesebb feladat lett volna, mint a mostani. Persze a feladatkitűzők nem ennyire kreatívak.

[13] vbalint	2011-06-11 18:28:22
Kinek sikerült megoldania a mostani hatpontos feladatot? Én azt hittem, csak két egyszerű integrálás, de azzal az jött ki, hogy független d-től, ami meglepne. :)

[12] patba

2011-01-02 17:33:28

Elsőt én is így csináltam, csak egy idővel az ionok újra szétválasztódnak, aztán megint lehet meríteni, ezt a pluszenergiát nem tudtam sehogy sem belevenni, bár ez már lehet, hogy elhanyagolható az első lemerítéskori energiához képest.

Másodikat viszont én nem így csináltam, az miért jogos feltevés, hogy azonos a nyomás? Először én is így próbáltam, de ez így nagyon nem négy pontos feladat. Ugye a szauna ajtaja nem záródik tökéletesen. Az egyensúly beálltakor a kis réseken a be-, és kilépő részecskék száma azonos. $\Delta$ t idő alatt egy bizonyos térrészben levő molekulák haladnak át a résen, és a két így meghatározott térfogatrészben azonos számú molekula kell, hogy legyen, ami áthalad.(Lehet, hogy itt ez hiba, mert az adott térfogatrészben a molekuláknak nem biztos, hogy ugyanolyan százaléka éri el a rést épp a sebességkülönbség miatt, de lehet, hogy mégis...). Így viszont az adódik, hogy $\frac{p_1}{p_2}=\sqrt{\frac{T_1}{T_2}}$ . De ehhez szükséges, hogy a szauna egy, a koncertteremmel megegyező hőmérsékletű teremben legyen, amit viszont nem biztosít egyértelműen a feladat szövege.

Előzmény: [11] Szabó Attila, 2011-01-02 17:12:40

[11] Szabó Attila

2011-01-02 17:12:40

1. pl. így: az elemet ismert ellenálláson lemerítjük, eközben rendszeresen mérjük az áramot, majd ezután a teljesítményt (I²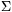 $\Sigma$ R) az idő szerint numerikusan integráljuk, ez adja az energiát. Nem a legjobb (az elemet menthetetlenül elhasználjuk), de mérni lehet vele.

2. a belső energia $\frac{f}2pV$ képletét használva (és feltéve, hogy a nyomás a két helyen egyforma; ez viszont jogos) a hőmérsékletadatoktól függetlenül kijön a megoldás.

Előzmény: [10] patba, 2010-12-18 19:56:33

[10] patba

2010-12-18 19:56:33

A novemberi fizikás feladatokhoz lenne két kérdésem.

1.) Egy gombelem által tárolt elektromos energiát hogyan határoznátok meg?

2.)P. 4293.-hoz ugyan van megoldásom, de érdekelne, hogy hogyan lehet még kiszámolni.(Illetve, hogy megoldható-e anélkül a feltevés nélkül, hogy a szauna kb 20°C-os teremben van)

Köszönöm

[9] Geg

2010-12-11 20:09:38

Egyebkent rendesen utanagondolva a sugariranyu sebesseg kiszamitasa sem olyan veszes.

Mivel az erot

$\vec{F}=\frac{1}{r}\frac{dA}{dt}\vec{e}_{\phi}$

alakba lehet irni ( $\vec{e}_{\phi}$ az erintoiranyu egysegvektor), a Newton egyenlet szerint

$\frac{1}{r}\frac{dA}{dt}\vec{e}_{\phi}=m \frac{d \vec{v}}{dt}=\Big(m\frac{d v_r}{dt}-m v_{\phi} \frac{d \phi}{dt}\Big)\vec{e}_{r}+\Big(m v_r \frac{d \phi}{dt}+m\frac{d v_{\phi}}{dt}\Big) \vec{e}_{\phi},$

ahol $\vec{e}_r$ ertelemszeruen a sugariranyu egysegvektor, a sebesseg $\vec{v}=v_r \vec{e}_r+v_{\phi} \vec{e}_{\phi}$ es ki van hasznalva, hogy

$\frac{d \vec{e}_r}{dt}=\vec{e}_{\phi} \frac{d\phi}{dt},\qquad \frac{d \vec{e}_{\phi}}{dt}=-\vec{e}_r \frac{d\phi}{dt}.$

A Newton egyenlet erinto iranyu resze

$\frac{1}{r}\frac{dA}{dt}=m v_r \frac{d\phi}{dt}+m \frac{d v_{\phi}}{dt},$

ami ekvivalens a perdulettetellel, ami alabb mar szerepelt es amibol kovetkezik, hogy

$A=mr^2\frac{d\phi}{dt}.$

A sugar iranyu komponensekre vonatkozo egyenloseg pedig

$0 = \frac{d v_r}{dt}-r \Big(\frac{d\phi}{dt}\Big)^2.$

Az utobbi ket osszefuggest osszekombinalva

$\frac{d v_r}{dt}=\frac{d^2 r}{dt^2}=\frac{A^2}{m^2r^3}.$

Ebbol azonnal latszik, hogy v_r>0, a test nem fordulhat vissza, es valamilyen adott A(t) fuggvenyhez megkaphato az r(t), belole pedig a v_r(t) fuggveny (valoszinuleg csak geppel).

Persze lehet esszel is csinalni, nem ilyen favago modon, mert minden idopillanatban be lehet ulni egy, az erinto iranyu sebesseg altal kijelolt egyenletesen forgo vonatkoztatasi rendszerbe, ahol a konstrukcio szerint nincs Coriolis-, csak centrifugalis ero, vagyis a sugariranyu mozgasegyenlet

$m \frac{dv_r}{dt}=m r \Big(\frac{d \phi}{dt}\Big)^2,$

ami megegyezik a korabbiakkal.

[8] Geg	2010-12-11 17:34:55
Persze, bocs! Tok jo a megoldas!
Előzmény: [7] jonas, 2010-12-11 17:17:07

[7] jonas	2010-12-11 17:17:07
Pörgess meg egy követ parittyával, aztán ereszd el, majd kérdezd meg, miért távolodik tőled sugárirányban.
Előzmény: [6] Geg, 2010-12-11 13:51:27

[6] Geg	2010-12-11 13:51:27
Ha a test mindig erintoiranyba gyorsul, hogyan kaphat sugariranyu sebesseget?
Előzmény: [5] Szabó Attila, 2010-12-11 12:38:44

[5] Szabó Attila

2010-12-11 12:38:44

A hatpontos megoldása:

Ismert, hogy 2r átmérőjéhez képest nagyon nagy $\ell$ hosszúságú és sűrűn tekercselt N menetes szolenoid mágneses indukciója a tekercsen kívül 0, azon belül a tekercs tengelyével párhuzamos, értéke $B=\mu_0\frac{IN}\ell$ .

Az elektromos mező a tekercs szimmetriája miatt nyilvánvalóan hengerszimmetrikus, s mivel a rendszerben nyugvó töltés nincs, így forrásmentes, azaz az elektromos térerősség érintőirányú és a síkban marad.

A P pont körüli R sugarú körre felírva Maxwell II. törvényét:

$E(R)2R\pi=-\frac{d\Phi}{dt}=-r^2\pi\frac{dB}{dt}=-r^2\pi\mu_0\frac{N}\ell\frac{dI}{dt}$

$E(R)=-\frac{r^2\mu_0N}{2\ell}\frac1R\frac{dI}{dt}$

A ponttöltésre ható erő nagysága:

$F=EQ=-\frac{r^2\mu_0NQ}{2\ell}\frac1R\frac{dI}{dt}$

A P pontra vonatkozó forgatónyomaték:

$M=FR=-\frac{r^2\mu_0NQ}{2\ell}\frac{dI}{dt}$

Felhasználva a perdülettételt:

$\frac{dN}{dt}=-\frac{r^2\mu_0NQ}{2\ell}\frac{dI}{dt}$

$dN=-\frac{r^2\mu_0NQ}{2\ell}dI$

Integrálva és figyelembe véve, hogy t=0-kor N és I is 0:

$N=-\frac{r^2\mu_0NQ}{2\ell}I$

A ponttöltés a P pontból nézve mindig érintőirányba gyorsul, azonban ehhez nem tartozik a középpont felé mutató gyorsulás, így a test gyorsulva távolodik a P ponttól, azaz a P ponttól mért távolság a folyamat végén nagyobb lesz mint kezdetben, valamint a testnek lesz a P ponttól elfelé mutató sebessége.

A perdület a folyamat végén 0 lesz, ami megkapható mv_mR alakban, ahol v_m a test érintőirányú sebessége. Mivel R nagyobb a kezdeti távolságnál, így N=0 csak akkor teljesülhet, ha v_m=0, azaz a testnek nincs érintőirányú sebessége.

A testnek tehát nincs érintőirányú, azonban van a P ponttól elmutató sebességkomponense, így P irányával a sebességvektor 180°-os szöget zár be. Ezt kerestük.

Megjegyzés. A feladat megoldása során sehol nem használtuk ki, hogy az áramerősség változása egyenletes, illetve pontosan a leírtak szerint zajlik. Tetszőleges áramerősség-idő függvény esetén 0 áramerősségnél a test sebessége a P pont irányával 180°-os szöget zár be.

[4] vbalint	2010-12-11 10:00:12
Kinek sikerült megoldania a hatpontos feladatot?

[3] Jedy	2010-10-12 20:28:49
Persze igazad van,de akinek esetleg a levezetése is megvan a feladatnak nem csak a megoldása,(vagy egysoros megoldása kérem ha lehetséges írja meg nekem).Köszönöm
Előzmény: [2] Nánási József, 2010-10-12 17:59:56

[2] Nánási József	2010-10-12 17:59:56
Szervusz! ha vársz egy kis időt, akkor felkerülnek a hivatalos megoldások.

[1] Jedy

2010-10-12 16:57:52

Kedves Fórumozók!

Abban szeretném a segítségeteket kérni,amennyiben lehetséges lejárt határidejű fizika feladatok megoldását töltsétek fel erre a fórumra(elméleti és mérési feladat egyaránt érdekel).Kiváltképpen fordulok azokhoz akik online küldik be megoldásukat,kérem őket másolják be(természetesen beadási határidő után).Előre is köszönöm minden kedves megoldásfeltöltőnek.

Már regisztráltál?
Új vendég vagy?