|
| [17] marcius8 | 2019-10-23 11:07:01 |
 Az A0B0C0 szabályos háromszög q0 oldala a következő képlettel számolható ki, ahol R az ABC háromszög köré írt kör sugara:
q0=8Rsin(α3)sin(β3)sin(γ3)
Az AA0BB0CC0 szabályos háromszög q oldala a következő képlettel számolható ki, ahol R az ABC háromszög köré írt kör sugara:
q=8Rsin(60°−α3)sin(60°−β3)sin(60°−γ3)
Az AA0BA0CA0 szabályos háromszög qA oldala a következő képlettel számolható ki, ahol R az ABC háromszög köré írt kör sugara:
qA=8Rsin(α3)sin(60°−β3)sin(60°−γ3)
Az AB0BB0CB0 szabályos háromszög qB oldala a következő képlettel számolható ki, ahol R az ABC háromszög köré írt kör sugara:
qB=8Rsin(60°−α3)sin(β3)sin(60°−γ3)
Az AC0BC0CC0 szabályos háromszög q0 oldala a következő képlettel számolható ki, ahol R az ABC háromszög köré írt kör sugara:
q0=8Rsin(60°−α3)sin(60°−β3)sin(γ3)
|
 |
|
| [16] marcius8 | 2019-10-23 11:05:29 |
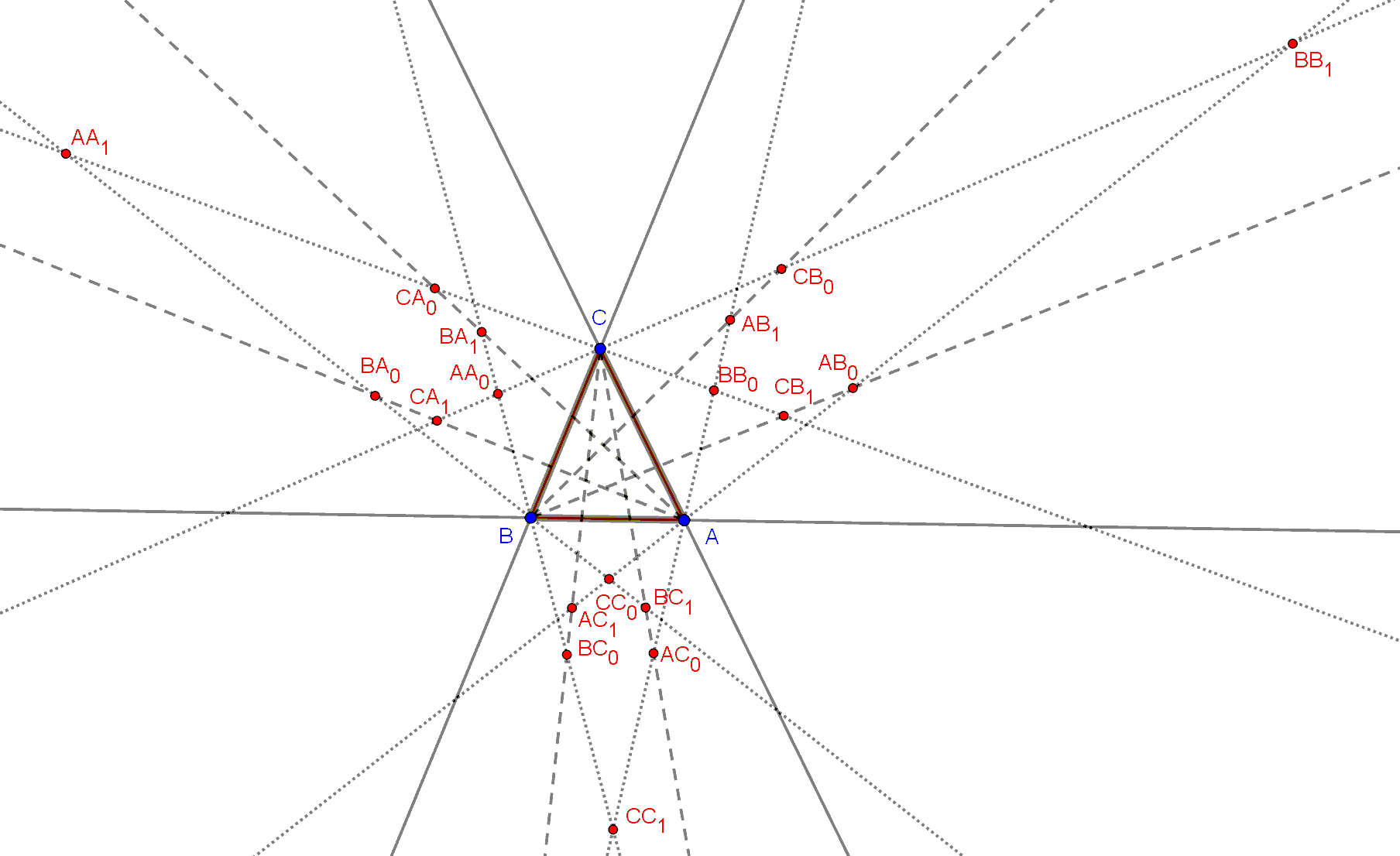
 Morley-tétel kibővítése:
Ezt a tételt nem csak az ABC belső szögharmadolóira lehet kimondani, hasonló állítások érvényesek az ABC külső szögharmadolóira is.
A továbbiakban a következő jelöléseket alkalmazom:
| Legyen AA0 a háromszög B csúcsából kiinduló, a oldala felőli, a oldalához közelebbi külső szögharmadoló félegyenesnek, és a háromszög C csúcsából kiinduló, a oldala felőli, a oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen AB0 a háromszög B csúcsából kiinduló, c oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög A csúcsából kiinduló, b oldala felőli, b oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen AC0 a háromszög C csúcsából kiinduló, b oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög A csúcsából kiinduló, c oldala felőli, c oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. |
| Legyen BA0 a háromszög A csúcsából kiinduló, c oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög B csúcsából kiinduló, a oldala felőli, a oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen BB0 a háromszög C csúcsából kiinduló, b oldala felőli, b oldalához közelebbi külső szögharmadoló félegyenesnek, és a háromszög A csúcsából kiinduló, b oldala felőli, b oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen BC0 a háromszög C csúcsából kiinduló, a oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög B csúcsából kiinduló, c oldala felőli, c oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. |
| Legyen CA0 a háromszög A csúcsából kiinduló, b oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög C csúcsából kiinduló, a oldala felőli, a oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen CB0 a háromszög B csúcsából kiinduló, a oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög C csúcsából kiinduló, b oldala felőli, b oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen CC0 a háromszög A csúcsából kiinduló, c oldala felőli, c oldalához közelebbi külső szögharmadoló félegyenesnek, és a háromszög B csúcsából kiinduló, c oldala felőli, c oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. |
Továbbá:
| Legyen AA1 a háromszög B csúcsából kiinduló, a oldala felőli, a oldalától távolabbi külső szögharmadoló félegyenesnek, és a háromszög C csúcsából kiinduló, a oldala felőli, a oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen AB1 a háromszög B csúcsából kiinduló, a oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög A csúcsából kiinduló, b oldala felőli, b oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen AC1 a háromszög C csúcsából kiinduló, a oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög A csúcsából kiinduló, c oldala felőli, c oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. |
| Legyen BA1 a háromszög A csúcsából kiinduló, b oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög B csúcsából kiinduló, a oldala felőli, a oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen BB1 a háromszög C csúcsából kiinduló, b oldala felőli, b oldalától távolabbi külső szögharmadoló félegyenesnek, és a háromszög A csúcsából kiinduló, b oldala felőli, b oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen BC1 a háromszög C csúcsából kiinduló, b oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög B csúcsából kiinduló, c oldala felőli, c oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. |
| Legyen CA1 a háromszög A csúcsából kiinduló, c oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög C csúcsából kiinduló, a oldala felőli, a oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen CB1 a háromszög B csúcsából kiinduló, c oldalához közelebbi belső szögharmadoló félegyenesnek, és a háromszög C csúcsából kiinduló, b oldala felőli, b oldalához közelebbi külső szögharmadoló félegyenesnek a metszéspontja. | Legyen CC1 a háromszög A csúcsából kiinduló, c oldala felőli, c oldalától távolabbi külső szögharmadoló félegyenesnek, és a háromszög B csúcsából kiinduló, c oldala felőli, c oldalától távolabbi külső szögharmadoló félegyenesnek a metszéspontja. |
|
 |
|
| [15] marcius8 | 2019-10-23 11:03:15 |
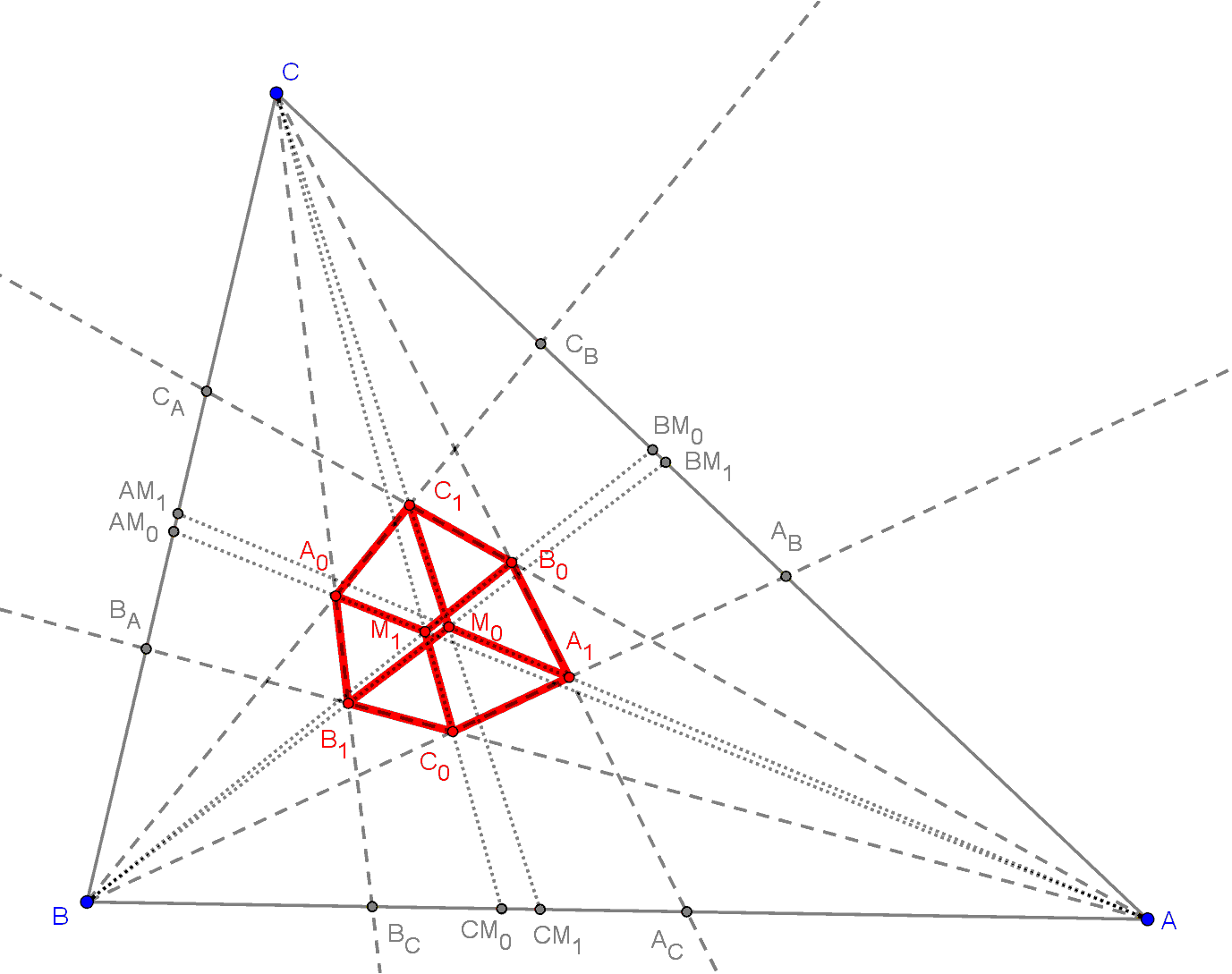
 Tekintsük az A0, B0, C0, M0, A1, B1, C1 M1 pontokat.
Az előbbi tételek alapján a következő állítások teljesülnek:
| Az M0A1 szakasz rajta van az AM1A egyenesen, amely átmegy az A ponton. | Az A0M1 szakasz rajta van az AM0A egyenesen, amely átmegy az A ponton. | Az B0C1 szakasz rajta van az CAA egyenesen, amely átmegy az A ponton. | Az C0B1 szakasz rajta van az BAA egyenesen, amely átmegy az A ponton. |
| Az M0B1 szakasz rajta van az BM1B egyenesen, amely átmegy az B ponton. | Az B0M1 szakasz rajta van az BM0B egyenesen, amely átmegy az B ponton. | Az C0A1 szakasz rajta van az ABB egyenesen, amely átmegy az B ponton. | Az A0C1 szakasz rajta van az CBB egyenesen, amely átmegy az B ponton. |
| Az M0C1 szakasz rajta van az CM1C egyenesen, amely átmegy az C ponton. | Az C0M1 szakasz rajta van az CM0C egyenesen, amely átmegy az C ponton. | Az A0B1 szakasz rajta van az BCC egyenesen, amely átmegy az C ponton. | Az B0A1 szakasz rajta van az ACC egyenesen, amely átmegy az C ponton. |
Ekkor a Morley-tétel a következőképpen értelmezhető: Hegyesszögű ABC háromszög esetén van olyan O pont, melyre teljesül, hogy OA, OB, OC szakaszok páronként merőlegesek legyenek egymásra. Ekkor van olyan A∗0B∗0C∗0M∗0A∗1B∗1C∗1M∗1 téglatest, amelynek A∗0, B∗0, C∗0, M∗0, A∗1, B∗1, C∗1, M∗1 csúcsainak az O pontra vonatkozó, és az ABC háromszög síkjára eső három iránypontos perspektív képe éppen az A0, B0, C0, M0, A1, B1, C1, M1 pontok lesznek. Ekkor ez a három iránypont éppen az ABC háromszög A, B, C csúcspontja. Ekkor a következő állítások teljesülnek az említett téglatest éleire:
Az M∗0A∗1, A∗0M∗1, B∗0C∗1, C∗0B∗1 szakaszok párhuzamosak az OA szakasszal.
Az M∗0B∗1, B∗0M∗1, C∗0A∗1, A∗0C∗1 szakaszok párhuzamosak az OB szakasszal.
Az M∗0C∗1, C∗0M∗1, A∗0B∗1, B∗0A∗1 szakaszok párhuzamosak az OC szakasszal.
Legyen a=→OA.
Legyen b=→OB.
Legyen c=→OC.
Ekkor baricentrikus koordinátákat használva, a következő összefüggések írhatóak fel:
A0=+a∗a+2bcos(γ3)∗b+2ccos(β3)∗c+a+2bcos(γ3)+2ccos(β3)
B0=+2acos(γ3)∗a+b∗b+2ccos(α3)∗c+2acos(γ3)+b+2ccos(α3)
C0=+2acos(β3)∗a+2bcos(α3)∗b+c∗c+2acos(β3)+2bcos(α3)+c
M0=+acos(α3)∗a+bcos(β3)∗b+ccos(γ3)∗c+acos(α3)+bcos(β3)+ccos(γ3)
A1=+2a∗a+bcos(γ3)∗b+ccos(β3)∗c+2a+bcos(γ3)+ccos(β3)
B1=+acos(γ3)∗a+2b∗b+ccos(α3)∗c+acos(γ3)+2b+ccos(α3)
C1=+acos(β3)∗a+bcos(α3)∗b+2c∗c+acos(β3)+bcos(α3)+2c
M1=+acos(α3)∗a+bcos(β3)∗b+ccos(γ3)∗c+acos(α3)+bcos(β3)+ccos(γ3)
|
 |
|
| [14] marcius8 | 2019-10-23 10:58:03 |
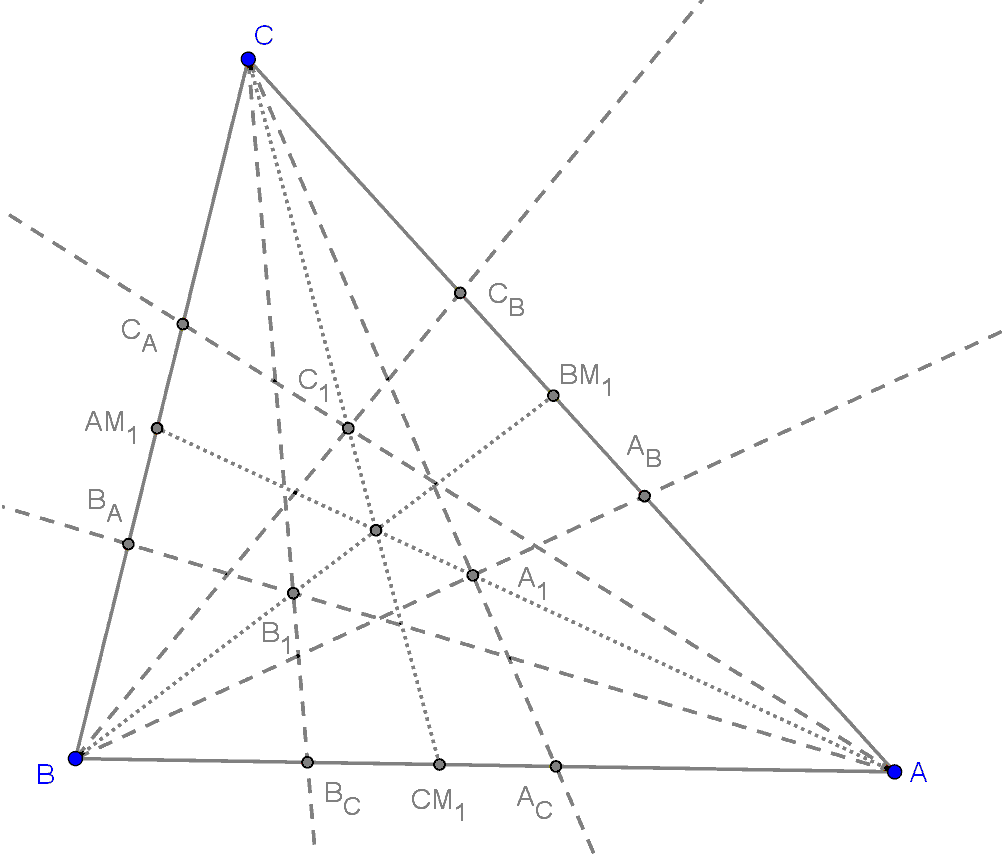
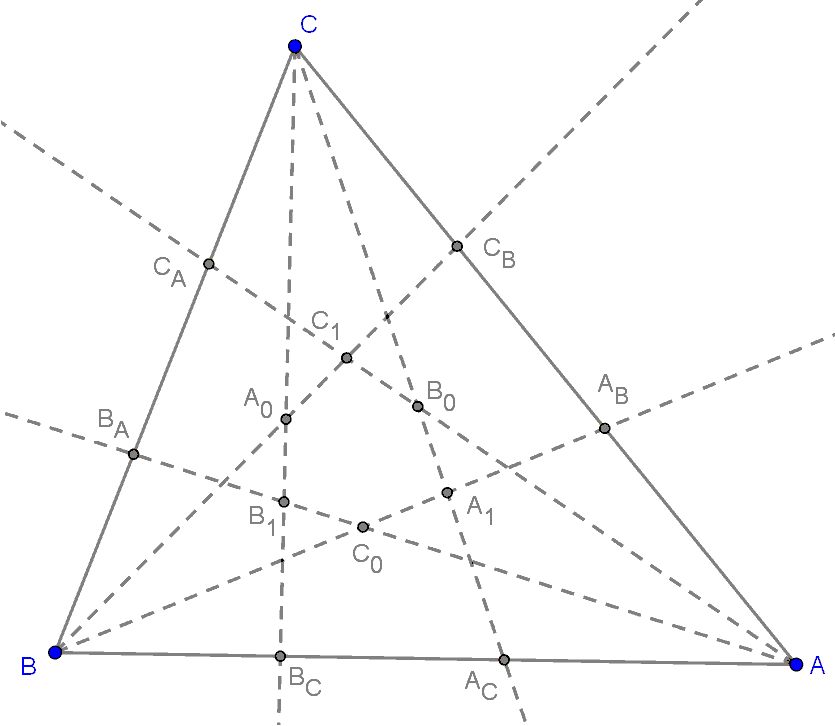
 Tétel: Az AA1, BB1, CC1 egyenesek egy pontban metszik egymást.
xxxxxxxxxx
Bizonyítás:
Legyen AM1 egyenes az AA1 egyenes és az ABC háromszög a oldalának metszéspontja.
Legyen BM1 egyenes az BB1 egyenes és az ABC háromszög b oldalának metszéspontja.
Legyen CM1 egyenes az CC1 egyenes és az ABC háromszög c oldalának metszéspontja.
Így azt kell bizonyítani, hogy az AM1, BM1, CM1 egyenesek egy pontban metszik egymást.
Az A1 pont rajta van a CAC, BAB, AAM1 egyeneseken, így a Ceva-tétel és a segédtételben bizonyított összefüggések miatt a következő összefüggés írható fel:
BAM1AM1C∗CABABA∗AACACB=1⇒
⇒BAM1AM1C=ABACAB∗ACBAAC=c2acos(β3)∗2acos(γ3)b=ccos(γ3)bcos(β3)
Az B1 pont rajta van a ABA, CBC, BBM1 egyeneseken, így a Ceva-tétel és a segédtételben bizonyított összefüggések miatt a következő összefüggés írható fel:
CBM1BM1A∗ABCBCB∗BBABAC=1⇒
⇒CBM1BM1A=BCBABC∗BACBBA=a2bcos(γ3)∗2bcos(α3)c=acos(α3)ccos(γ3)
Az C1 pont rajta van a BCB, ACA, CCM1 egyeneseken, így a Ceva-tétel és a segédtételben bizonyított összefüggések miatt a következő összefüggés írható fel:
ACM1CM1B∗BCACAC∗CCBCBA=1⇒
⇒ACM1CM1B=CACBCA∗CBACCB=b2ccos(α3)∗2ccos(β3)a=bcos(β3)acos(α3)
A most felírt összefüggések segítségével a következő számítás végezhető el:
BAM1AM1C∗CBM1BM1A∗ACM1CM1B=ccos(γ3)bcos(β3)∗acos(α3)ccos(γ3)∗bcos(β3)acos(α3)=1
Így a Ceva-tétel miatt az AAM1, BBM1, CCM1 egyenesek egy pontban metszik egymást, azaz az AA1, BB1, CC1 egyenesek egy pontban metszik egymást. Legyen M0 ennek a három egyenesnek a metszéspontja.
|
 |
|
| [13] marcius8 | 2019-10-23 10:56:13 |
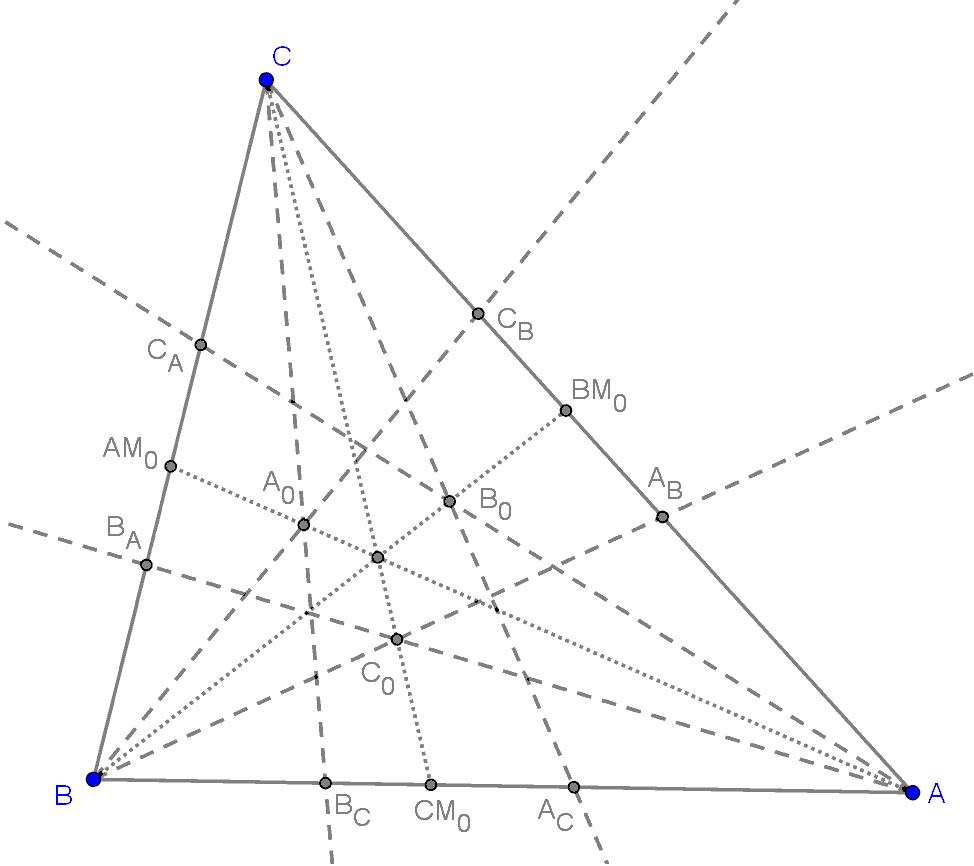
 Tétel: Az AA0, BB0, CC0 egyenesek egy pontban metszik egymást.
xxxxxxxx
Bizonyítás:
Legyen AM0 egyenes az AA0 egyenes és az ABC háromszög a oldalának metszéspontja.
Legyen BM0 egyenes az BB0 egyenes és az ABC háromszög b oldalának metszéspontja.
Legyen CM0 egyenes az CC0 egyenes és az ABC háromszög c oldalának metszéspontja.
Így azt kell bizonyítani, hogy az AM0, BM0, CM0 egyenesek egy pontban metszik egymást.
Az A0 pont rajta van a CBC, BCB, AAM0, egyeneseken, így a Ceva-tétel és a segédtételben bizonyított összefüggések miatt a következő összefüggés írható fel:
BAM0AM0C∗CCBCBA∗ABCBCB=1⇒
⇒BAM0AM0C=CBACCB∗BCBABC=2ccos(β3)a∗a2bcos(γ3)=ccos(β3)bcos(γ3)
Az B0 pont rajta van a ACA, CAC, BBM0, egyeneseken, így a Ceva-tétel és a segédtételben bizonyított összefüggések miatt a következő összefüggés írható fel:
CBM0BM0A∗AACACB∗BCACAC=1⇒
⇒CBM0BM0A=ACBAAC∗CACBCA=2acos(γ3)b∗b2ccos(α3)=acos(γ3)ccos(α3)
Az C0 pont rajta van a BAB, ABA, CCM0, egyeneseken, így a Ceva-tétel és a segédtételben bizonyított összefüggések miatt a következő összefüggés írható fel:
ACM0CM0B∗BBABAC∗CABABA=1⇒
⇒ACM0CM0B=BACBBA∗ABACAB=2bcos(α3)c∗c2acos(β3)=bcos(α3)acos(β3)
A most felírt összefüggések alapján a következő számítás végezhető el:
BAM0AM0C∗CBM0BM0A∗ACM0CM0B=ccos(β3)bcos(γ3)∗acos(γ3)ccos(α3)∗bcos(α3)acos(β3)=1
Így a Ceva-tétel miatt az AAM0, BBM0, CCM0 egyenesek egy pontban metszik egymást, azaz az AA0, BB0, CC0 egyenesek egy pontban metszik egymást. Legyen M1 ennek a három egyenesnek a metszéspontja.
|
 |
|
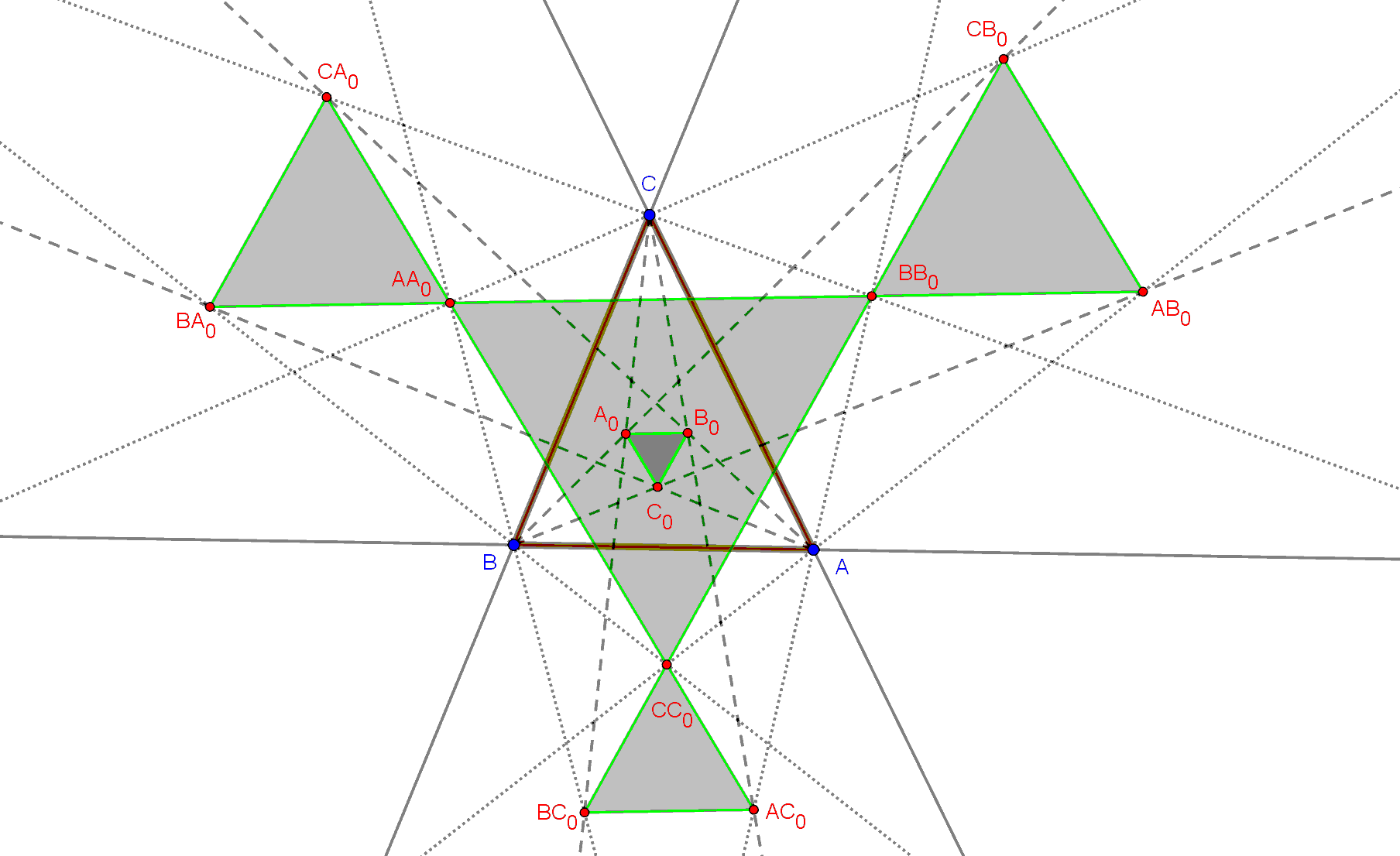
| [12] marcius8 | 2019-10-23 10:52:18 |
 Amit a Morley-tétellel kapcsolatban észrevettem:
A továbbiakban a következő jelöléseket használom:
Legyenek az ABC háromszög szögei: α, β, γ, és legyenek az ABC háromszög olalai: a, b, c.
xxxxxxxxxx
| Az ABC háromszög A csúcsából kiinduló, B csúcshoz közelebbi szögharmadoló egyenes az a oldalt a BA pontban metszi. | Az ABC háromszög A csúcsából kiinduló, C csúcshoz közelebbi szögharmadoló egyenes az a oldalt a CA pontban metszi. |
| Az ABC háromszög B csúcsából kiinduló, C csúcshoz közelebbi szögharmadoló egyenes az b oldalt a CB pontban metszi. | Az ABC háromszög B csúcsából kiinduló, A csúcshoz közelebbi szögharmadoló egyenes az b oldalt a AB pontban metszi. |
| Az ABC háromszög C csúcsából kiinduló, A csúcshoz közelebbi szögharmadoló egyenes az c oldalt a AC pontban metszi. | Az ABC háromszög C csúcsából kiinduló, B csúcshoz közelebbi szögharmadoló egyenes az c oldalt a BC pontban metszi. |
xxxxxxxxxx
| Legyen A0 az ABC háromszög a oldalához közelebbi BCB és CBC szögharmadolók metszéspontja. | Legyen B0 az ABC háromszög b oldalához közelebbi CAC és ACA szögharmadolók metszéspontja. | Legyen C0 az ABC háromszög c oldalához közelebbi ABA és BAB szögharmadolók metszéspontja. |
| Legyen A1 az ABC háromszög a oldalától távolabbi BAB és CAC szögharmadolók metszéspontja. | Legyen B1 az ABC háromszög b oldalától távolabbi CBC és ABA szögharmadolók metszéspontja. | Legyen C1 az ABC háromszög c oldalától távolabbi ACA és BCB szögharmadolók metszéspontja. |
Segédtétel:
| BACAAC=2a∗cos(γ3)b | CBABBA=2b∗cos(α3)c | ACBCCB=2c∗cos(β3)a |
| ABCBBC=2b∗cos(γ3)a | BCACCA=2c∗cos(α3)b | CABAAB=2a∗cos(β3)c |
Ezek az összefüggések trigonometrikus számításokkal (szinusztétel, koszinusztétel, addíciós tétel) bizonyíthatóak.
Legyen O egy tetszőlegesen rögzített pont valahol az ABC háromszög síkján kívül.
Legyen a=→OA.
Legyen b=→OB.
Legyen c=→OC.
Ekkor baricentrikus koordinátákat használva, a következő összefüggések írhatóak fel:
| →OAB=2acos(β3)∗a+c∗c2acos(β3)+c | →OBC=2bcos(γ3)∗b+a∗a2bcos(γ3)+a | →OCA=2ccos(α3)∗c+b∗b2ccos(α3)+b |
| →OBA=2bcos(α3)∗b+c∗c2bcos(α3)+c | →OCB=2ccos(β3)∗c+a∗a2ccos(β3)+a | →OAC=2acos(γ3)∗a+b∗b2acos(γ3)+b |
|
 |
|
| [11] Prof. Mózes | 2013-09-25 20:06:42 |
 Az alábbi prezentációban szó esik arról, hogy miként lehet papírhajtogatással szöget harmadolni. De az is kiderül, hogy különleges görbékkel vagy betolóvonalzóval is elvégezhető a szögharmadolás:
Gáspár Merse Előd - 2010.07.19 - BERZETÖK önképző tábor - A papírhajtogatás matematikája.pdf
Az előadást megtaláljátok a neten, a linket csak azért nem tudtam berakni, mert nem engedte a különleges karaktereket megjeleníteni.
|
|
| [10] Sinobi | 2013-06-04 21:39:17 |
 Néhány egyszerű egykaptafa csinálmány feladat:
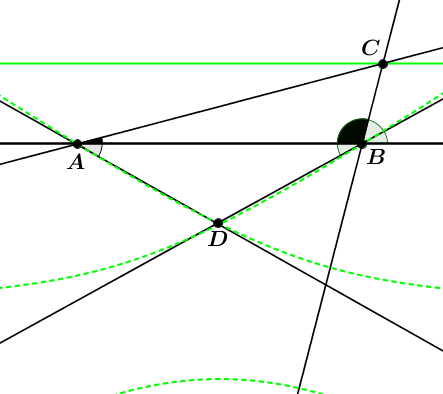
Ha ABC háromszögben C mozog, mit lehet tudni az A illetve B csúcsbeli szögharmadolók metszéspontjáról?
Rögzítsük A és B pontot. C fusson egy AB egyenesre merőleges/párhuzamos egyenesen, D legyen CAB és CBA szögharmadolóinak közelebbiknek/távolabbiknak a metszéspontja. Hol helyezkedik el D? Szerkesszünk olyan C pontot, hogy AD/CD párhuzamos legyen egy adott meredekségű egyenessel.
Amikor AC és BC a szögharmadolók, hol helyezkedik el a háromszög D csúcsa?
Legyen A és B pont rögzített, C futhat egy AB egyenesre merőleges/párhuzamos egyenesen. Legyen CA' egyenes ami átmegy A-n és CA' AB szög = 3 CAB, hasonlóan CB' egyenes átmegy B-n és CB' AB szög = 3 CBA, D ezek metszése. Szerkesszünk olyan C pontot, hogy AD/CD párhuzamos legyen egy adott meredekségű egyenessel / ABCD húrnégyszög legyen.
Amikor AB egyenes a szögharmadoló:
Legyen A B pont rögzített, C AB-re merőleges/párhuzamos egyenesen fusson. Legyen CA' egy A-n átmenő, AB-vel -2*CAB szöget bezáró egyenes, hasonlóan CB': átmegy B-n, AB-vel -2*CBA szöget zár be, D ezek metszéspontja. Szerkesszünk olyan C pontot, hogy AD/CD párhuzamos legyen egy adott egyenessel, ABCD húrnégyszög legyen.
Ez az eset valamivel érdekesebb, mint az előzők, itt még megfigyeléseket is lehet tenni D pályájával kapcsolatban. Lássuk be, hogyha C egy, AB-re merőleges egyenesen mozog, akkor D egy kúpszeletet ír le (ennek mondjuk Steiner-tételes vagy komplex függvényes lehet a megoldása), és lássuk be, hogyha C egy AB-vel párhuzamos egyenesen mozog, akkor D AB felezővonalán olyan távol lesz AB egyenestől, mint a C pont (lásd ábra)
|
 |
|
| [9] Sinobi | 2013-06-04 18:31:03 |
 ,,Még nem gondoltam át, de használható lehet, hogy egy belső és egy külső szög harmadolóegyeneseinek szögei 60 fokosak, "
hogyan?
|
| Előzmény: [3] w, 2013-01-14 21:24:32 |
|
| [8] w | 2013-04-30 18:52:28 |
 Igen, ez a nemrég (talán a Nehezebb Problémák témában)emlegetett Galois-elmélet eredménye. Különösen szellemesnek tartom a "tomahawkos" szerkesztést. Itt.
|
| Előzmény: [5] marcius8, 2013-01-17 09:59:46 |
|
|
|
| [5] marcius8 | 2013-01-17 09:59:46 |
 Még egyszer tisztelettel köszöntöm az eddigi hozzászólókat!!!
Azért tartom fontosnak a szögharmadolókra vonatkozó tételeket, mert geometriai szerkesztések során az euklideszi szerkesztési lépések a hivatalosan engedélyezettek, és ezek között nem szerepel a szögharmadolás. Így sok-sok matematikus csak azokat a geometriai alakzatokat vizsgálta, amelyek euklideszi szerkesztési szabályok szerint szerkeszthetőek. Pedig a szögharmadolás sem bonyolult szerkesztés (megtalálható az interneten). Így érdemes kutakodni a szögharmadolók körül, mert szerintem rengeteg tétel vár még felfedezésre.
Harmadfokú szerkesztésnek nevezem egy a racionális számok halmazában nem felbontható racionális együtthatójú polinom gyökének megszerkesztését. Így egy adott szög szerkesztése is harmadfokú szerkesztés, csakúgy mint a "déloszi probléma megoldása" és a "szabályos 7-szög szerkesztése". (Ezekről a témákról is található információ az interneten.) Szintén ilyen harmadfokú szerkesztés három szakasz mértani közepének szerkesztése (a "déloszi probléma" általánosítása). Itt megjegyzem, hogy aki tudja három szakasz számtani, mértani, harmonikus és más közepének kapcsolatát geometriai ábrán szemléltetni, azt kérem, hogy tegye közzé a fórumban. (Nekem három nem negatív szám számtani és harmónikus közepe közötti kapcsolatot sikerült szemléltetni geometriailag.)
Rengeteg geometriai probléma van, amelynek megoldása harmadfokú egyenlet megoldását jelenti. Ezt is azért tartom fontosnak megemlíteni, mert az euklideszi szerkesztési szabályok gyakori használata miatt sokan csak olyan problémát vizsgálnak, amelyeknek megoldása másodfokú egyenletek megoldását jelenti. Ha valakit érdekel, szívesen írok olyan geometriai problémát, amelynek megoldása harmadfokú egyenlet megoldását jelenti. Például egy ilyen: Adott a síkon két egymásra merőleges egyenes, és adott egy pont, amelyik az egyik adott egyenestől "p" távol van, a másik adott egyenestől "q" távol van. Szerkesztendő olyan egyenes, amely átmegy az adott ponton és amelynek a két adott egyenes közötti részének hossza "d".
|
|
| [4] marcius8 | 2013-01-17 08:06:56 |
 Tisztelettel köszöntöm az eddigi hozzászólókat!
Sakkmath szögharmadolókra vonatkozó tétele egy érdekes állítást fogalmaz meg, de ha jól meggondoljuk, ez nem csak szögharmadolókra vonatkozik. Ugyanis tetszőleges szög-"n"-edelők esetén a rombusz belsejében keletkezett négyszög tengelyesen szimmetrikus kell legyen a rombusz egymást merőlegesen felező átlóira, és akkor ez a négyszög csag a téglalap lehet. Mindenesetre nagyon szépen köszönöm Sakkmath fórumozónak ezt az állítást. Olyan tételt kellene keresni, amely csak a szögharmadolókra vonatkozik.
W fórumozó által felvetett kérdésre a válaszom, hogy mindenfajta szinusztétellel, koszinusztétellel, addíciós tétellel ki lehet számolni a kérdezett arányokat, ez nem is túl nehéz feladat. Továbbá régebben volt egy kömal-feladat,mely szerint bizonyítandó, hogy egy háromszög egy csúcsából kiinduló belső szögharmadoló egyenesek a csúccsal szemközti oldalt olyan szakaszokra osztják, melyek közül a két szélső szakasz számtani közepe nagyobb, mint a középső szakasz. Én ezen egy kicsit túl mentem, mert sikerült azt is belátni, hogy egy háromszög egy csúcsából kiinduló belső szögharmadoló egyenesek a csúccsal szemközti oldalt olyan szakaszokra osztják, melyek közül a két szélső szakasz mértani közepe nagyobb, mint a középső szakasz. Ezt a két állítást sem túl nehéz bizonyítani.
|
|
| [3] w | 2013-01-14 21:24:32 |
 Számoljuk ki, milyen arányban osztja egy háromszög egyik szögének harmadoló félegyenesei a szemközti oldalt!
Még nem gondoltam át, de használható lehet, hogy egy belső és egy külső szög harmadolóegyeneseinek szögei 60 fokosak, talán később ki lehetne erre egy feladatot is ötleni.
|
|
| [2] sakkmath | 2013-01-12 22:45:06 |
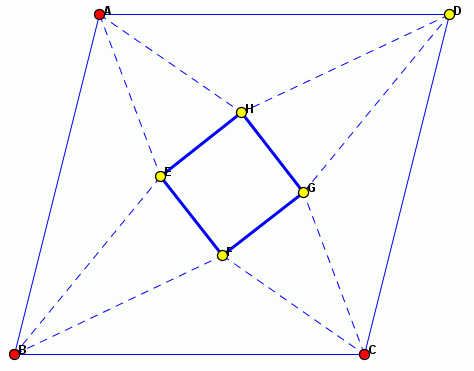
 1. tétel: Bármely rombusz szomszédos szögharmadoló egyeneseinek metszéspontjai egy téglalap csúcspontjai.
(Ha szögharmadolók helyett szögnegyedelőket írunk, akkor a metszéspontok négyzetet alkotnak.)
Ábra:
|
 |
| Előzmény: [1] marcius8, 2013-01-11 16:06:54 |
|
| [1] marcius8 | 2013-01-11 16:06:54 |
 Nagyon kevés tételt ismerek háromszög vagy négy szög szögharmadolóira, ilyen például a Morley-tétel. Ha valaki tud szögharmadolásra vonatkozó tételt, kérem írjon erre a fórumra.
|
|
