|
| [182] Róbert Gida | 2014-02-15 01:17:00 |
 Kicsit átírva: ![H(s_1,...,s_{k_0},s'_1,...,s'_{k_0})=\sum_{d_1,...,d_{k_0},d'_1,...,d'_{k_0}}\prod_{j=1}^{k_0}\mu (d_j)\mu (d'_j)\frac{d_j^{-(1+is_j)/\log R}d'_j^{-(1+is'_j)/\log R}}{[d_j,d'j]}](/kep/keplet.cgi?k=980CA7CCBE4BA7FA)
ha [dj,d'j] páronként relatív prímek, akkor rögzített p prím csak legfeljebb az egyik dj,d'j párt oszthatja. És azokat is csak első hatványon, hiszen különben  (dj) (dj) (d'j)=0 volna, ekkor a szorzat is nulla. Így, a nagy szummában adott p prímre 4 lehetőség van: dj,d'j egyikét sem osztja p, pontosan egyiket osztja (dj vagy d'j), vagy mindkettőt (és ezen utóbbi esetekben ekkor más d,d' taghoz rel. prím). (d'j)=0 volna, ekkor a szorzat is nulla. Így, a nagy szummában adott p prímre 4 lehetőség van: dj,d'j egyikét sem osztja p, pontosan egyiket osztja (dj vagy d'j), vagy mindkettőt (és ezen utóbbi esetekben ekkor más d,d' taghoz rel. prím).
Ha egyiket osztja, akkor a szorzatban ennek  felel meg (vagy ugyanez vesszőssel), nevezőben a p tag az a legkisebb közös többszörösből jön, (-1) pedig a felel meg (vagy ugyanez vesszőssel), nevezőben a p tag az a legkisebb közös többszörösből jön, (-1) pedig a  (dj)-ből (ne feledjük: (dj)-ből (ne feledjük:  multiplikatív). Ha mindkét tagot osztja, akkor multiplikatív). Ha mindkét tagot osztja, akkor  , ha egyik tagot sem osztja p, akkor ennek 1 felel meg. És pontosan ez a 4 féle tag szerepel az Euler szorzat előállításánál. , ha egyik tagot sem osztja p, akkor ennek 1 felel meg. És pontosan ez a 4 féle tag szerepel az Euler szorzat előállításánál.
|
| Előzmény: [180] Maga Péter, 2014-02-09 17:20:48 |
|
|
| [180] Maga Péter | 2014-02-09 17:20:48 |
 Bő hónapos kihagyás után folytatom a bizonyítást.
Feladat. Bizonyítsuk be, hogy

vagyis a H függvénynek van egy Euler-szorzat előállítása, ami minden s1,...,sk0,s1',...,sk0' R-re érvényes. R-re érvényes.
Most ebből megbecsüljük H-t. Világos, hogy

Egészen konkrétan azt fogjuk belátni, hogy

(Figyelem! Itt a Tao-blogban van egy zavaró elírás.) Lehet, hogy erre van egyszerűbb is (és ha találtok, akkor írjátok meg!), én a következőt találtam ki. Nyilván 1+3p-1-1/log R (1+p-1-1/log R)3, így elég azt belátni, hogy (1+p-1-1/log R)3, így elég azt belátni, hogy

Itt a bal oldal nyilván kisebb, mint  (1+1/log R) (terjesszük ki a szorzást minden prímre, illetve 1+p-1-1/log R helyére írjunk 1+p-1-1/log R+p-2-2/log R+p-3-3/log R+...-t, nyilván nő a szorzat értéke). Ugyanakkor (1+1/log R) (terjesszük ki a szorzást minden prímre, illetve 1+p-1-1/log R helyére írjunk 1+p-1-1/log R+p-2-2/log R+p-3-3/log R+...-t, nyilván nő a szorzat értéke). Ugyanakkor  (1+1/log R) (1+1/log R)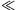 O(log R), hiszen O(log R), hiszen  (s)-1/(s-1) korlátos, amint s (s)-1/(s-1) korlátos, amint s 1 jobbról. 1 jobbról.
Mindez azt mutatja (figyelembe véve 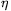 gyors lecsengését: ld. a [179]-es hozzászólásomat), hogy a kiszámítandó kettős integrálban ( gyors lecsengését: ld. a [179]-es hozzászólásomat), hogy a kiszámítandó kettős integrálban ( ) szorítkozhatunk a ) szorítkozhatunk a  tartományra: amit ezen kívül kapunk, az elhanyagolható (o(...)) ahhoz képest, amit kapni akarunk. tartományra: amit ezen kívül kapunk, az elhanyagolható (o(...)) ahhoz képest, amit kapni akarunk.
|
| Előzmény: [179] Maga Péter, 2014-01-08 13:09:13 |
|
| [179] Maga Péter | 2014-01-08 13:09:13 |
 Térjünk vissza ahhoz a konkrét f függvényhez, amit eddig használtunk, és terjesszük ki Rk0-ra kompakt tartójú sima függvényként, továbbra is f-fel jelöljük.
A Fourier-transzformáltról szóló kitekintés értelmében f olyan alakba írható, hogy

Ezt könnyű látni, vegyük f(t1,...,tk0) helyett az  függvényt, ez még mindig sima és kompakt tartójú, és legyen függvényt, ez még mindig sima és kompakt tartójú, és legyen 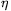 ennek Fourier-transzformáltja (a kitevőben -2 ennek Fourier-transzformáltja (a kitevőben -2 -k nélkül) szorozva 2 -k nélkül) szorozva 2 megfelelő hatványával. Az inverziós képlet éppen azt adja, amit szeretnénk. megfelelő hatványával. Az inverziós képlet éppen azt adja, amit szeretnénk.
Továbbá
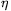 (s1,...,sk0) (s1,...,sk0)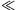 f,A(1+max (|s1|,...,|sk0|))-A f,A(1+max (|s1|,...,|sk0|))-A
minden A>0 számra, hiszen f sima és kompakt tartójú (és így  -szerese is). -szerese is).
Ennek segítségével a [176] utolsó képletének bal oldala abba az alakba írható, hogy

ahol
![H(s_1,...,s_{k_0},s_1',...,s_{k_0}')= \sum_{d_1,...,d_{k_0},d_1',...,d_{k_0}'} \left( \prod_{j=1}^{k_0} \mu(d_j)\mu(d_j') \right) \frac{\prod_{j=1}^{k_0} d_j^{-(1+is_j)/\log R}d_j'^{-(1+is_j')/\log R}}{[d_1,d_1']\cdot...\cdot[d_{k_0},d_{k_0}']},](keplet.cgi?k=BA9F1B87C8268C54)
ahol, emlékezzünk vissza, az összegzésben [d1,d1'],...,[dk0,dk0'] páronként relatív prímek.
|
| Előzmény: [176] Maga Péter, 2014-01-05 15:59:48 |
|
| [178] Maga Péter | 2014-01-08 12:17:07 |
 Kitekintés: a Fourier-transzformált néhány alaptulajdonsága.
A bizonyítás, mint említettem, nem egészen elemi. Szükségünk lesz a Fourier-transzformált néhány alaptulajdonságára, ezeket a következőkben összefoglalom. Legyen f:Rn C függvény, melyről feltesszük, hogy sima (akárhányszor deriválható), valamint kompakt tartójú (egy korlátos halmazon kívül 0). Ekkor Fourier-transzformáltján a következő, szintén Rn C függvény, melyről feltesszük, hogy sima (akárhányszor deriválható), valamint kompakt tartójú (egy korlátos halmazon kívül 0). Ekkor Fourier-transzformáltján a következő, szintén Rn C függvényt értjük: C függvényt értjük:

Az eredeti f függvény a Fourier-transzformáltból egyszerűen visszakapható az inverz transzformált segítségével:

ez lényegében egy újabb Fourier-transzformált, de azért figyeljünk az előjelre: f**(x)=f(-x).
Mivel f sima és kompakt tartójú, f* nagyon gyorsan lecseng:
f*( 1,..., 1,..., n) n)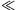 f,A(1+max (| f,A(1+max (| 1|,...,| 1|,...,| n|))-A n|))-A
minden A>0 számra (most az n dimenziós tér maximumnormáját használtam, de mivel bármelyik két norma ekvivalens, ugyanez igaz bármely más normára is). Ez lényegében parciális integrálás, például egy dimenzióban a | |>1 tartományon |>1 tartományon

ahol f [a,b]-n kívül 0. Ebből A=1-re világos az állítás: | |>1-re ezt a becslést használjuk, | |>1-re ezt a becslést használjuk, | | | 1-re pedig triviális. 1-re pedig triviális.
Bővebb leíráshoz nézzük meg ezt.
Sajnos a Fourier-transzformált normalizálása nem egészen egységes: helyenként a 2 vagy/és a - kimarad a kitevőből. Ezek nem vezetnek lényeges változáshoz, az inverz transzformált egy kicsit máshogy néz ki (az integrálban a változó lineáris helyettesítésével megkaphatók a különböző változatok). Én most a wikipedia normalizálását követtem, a Tao-poszthoz azt az alakot használjuk, amikor vagy/és a - kimarad a kitevőből. Ezek nem vezetnek lényeges változáshoz, az inverz transzformált egy kicsit máshogy néz ki (az integrálban a változó lineáris helyettesítésével megkaphatók a különböző változatok). Én most a wikipedia normalizálását követtem, a Tao-poszthoz azt az alakot használjuk, amikor

Ebben az esetben az inverz transzformált

|
| Előzmény: [176] Maga Péter, 2014-01-05 15:59:48 |
|
| [177] Róbert Gida | 2014-01-05 21:04:48 |
 Állítás: Gk(n) n*(1+log n)k-1, ahol n*(1+log n)k-1, ahol  , itt most Fk(n)-en a rendezett pozitív egész tagú felbontások számát értem. Triviálisan: G1(n)=n (hiszen F1(n)=1), továbbá, ha k>1, akkor , itt most Fk(n)-en a rendezett pozitív egész tagú felbontások számát értem. Triviálisan: G1(n)=n (hiszen F1(n)=1), továbbá, ha k>1, akkor ![G_k(n)=\sum _{d=1}^n G_{k-1} (\Big[ \frac nd \Big])](keplet.cgi?k=83CAE2DBDF6DE859) , ugyanis legyen i , ugyanis legyen i n egy felbontásában d az első tag, ekkor i osztható d-vel; i=d*x, az ilyen felbontások száma n egy felbontásában d az első tag, ekkor i osztható d-vel; i=d*x, az ilyen felbontások száma  , így , így ![G_{k-1}(\Big[ \frac nd \Big])](keplet.cgi?k=F86D7EF213B36A56) az olyan felbontások száma n-ig, ahol az első tényező d. Továbbá d 1..n lehet és minden k tagú felbontást egyszer számoltunk. Így (k-ra való) indukcióval: az olyan felbontások száma n-ig, ahol az első tényező d. Továbbá d 1..n lehet és minden k tagú felbontást egyszer számoltunk. Így (k-ra való) indukcióval:
![G_k(n)=\sum _{d=1}^n G_{k-1} (\Big[ \frac nd \Big])\le \sum _{d=1}^n \frac nd (1+\log (\frac nd))^{k-1} \le \sum _{d=1}^n \frac nd (1+\log n)^{k-1}=n*(1+\log n)^{k-1}*\sum_{d=1}^n \frac 1d \le n*(1+\log n)^k](keplet.cgi?k=3145354BB00EF7AC) , hiszen ismeretes: , hiszen ismeretes:  . .
Ezzel egész R=n értékre teljesül az állítás, míg ebből nem egész értékekre is egyszerűen látható.
|
| Előzmény: [176] Maga Péter, 2014-01-05 15:59:48 |
|
| [176] Maga Péter | 2014-01-05 15:59:48 |
 Az alkalmas súlyfüggvény felé II.
Elérkeztünk arra a pontra, ahol megmondjuk a súlyfüggvényt. Legyen tehát f sima függvény, mely eltűnik a  k0 szimplexen kívül. Mostantól azt is feltesszük, hogy f szimmetrikus, azaz k0 szimplexen kívül. Mostantól azt is feltesszük, hogy f szimmetrikus, azaz  , ha , ha 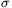 a {1,...,k0} halmaz egy permutációja. Ekkor legyen a {1,...,k0} halmaz egy permutációja. Ekkor legyen

Annyi mindenesetre világos, hogy ez tényleg nemnegatív, tényleg 'súlyfüggvény'.
Az (A) tulajdonság bizonyítása I.
A négyzetet kibontva és az összeget átrendezve
![\sum_{x\leq n\leq 2x} \nu(n)=\sum_{d_1,...,d_{k_0},d_1',...,d_{k_0}'} \left(\prod_{j=1}^{k_0}\mu(d_j)\mu(d_j')\right) f\left(\frac{\log d_1}{R},...,\frac{\log d_{k_0}}{R}\right) f\left(\frac{\log d_1'}{R},...,\frac{\log d_{k_0}'}{R}\right) \sum_{x\leq n\leq 2x:n\equiv b(W),\forall 1\leq j\leq k_0:[d_j,d_j']|(n+h_j)} 1.](keplet.cgi?k=4748D12D326DA5CC)
Állítjuk, hogy a belső, n feletti összegzésben n+hj és n+hj1 relatív prímek, ha 1 j<j1 j<j1 k0. Valóban, legyen indirekte p egy közös prímosztójuk. Ekkor p|hj1-hj, azaz p k0. Valóban, legyen indirekte p egy közös prímosztójuk. Ekkor p|hj1-hj, azaz p hk0. Mivel x nagy, p|W. Ugyanakkor a b maradékosztály olyan, hogy b+H relatív prím W-hez, ami ellentmondás. hk0. Mivel x nagy, p|W. Ugyanakkor a b maradékosztály olyan, hogy b+H relatív prím W-hez, ami ellentmondás.
Ez azt mutatja, hogy a belső (n feletti) összeg eltűnik, ha a [dj,dj']-k nem páronként relatív prímek. Azaz
![\sum_{x\leq n\leq 2x:n\equiv b(W),\forall 1\leq j\leq k_0:[d_j,d_j']|(n+h_j)} 1=\frac{x}{W[d_1,d_1']\cdot...\cdot[d_{k_0},d_{k_0}']}+O(1),](keplet.cgi?k=005E1D16BA536C52)
ahol O(1) egy korlátos mennyiséget jelöl (a konkrét értéke persze sok mindentől függ, lehet pozitív és negatív is, mindenesetre van rá abszolút korlát).
Nyilván az összeg akkor is eltűnik, ha valamelyik dj vagy dj' nagyobb, mint R, ezért mostantól feltesszük, hogy d1,...,dk0,d1',...,dk0' R. R.
Most megmutatjuk, hogy az O(1) hiba csak elhanyagolhatót ad, amint a dj-k és dj'-k felett összegzünk. Ez ugyanis összesen csak

ahol O(X) mindig X-szel osztva korlátos mennyiséget jelöl (emlékezzünk vissza: O(1) jelöli a korlátos mennyiséget). A belső összeghez tehát azt kell összeszámolni, hányféleképp bontható egy R-nél nem nagyobb egész szám k0 darab egész szám szorzatára. Ismét megpróbálkozok egy feladattal, hátha most lesznek megoldók, ez önmagában is érdekes.
Feladat. Legyen k rögzített pozitív egész. Jelöljük Fk(n)-nel azt a számot, ahányféleképpen fel lehet bontani n-et k egész szám szorzatára. Bizonyítsuk be, hogy

ahol logO(1)R alatt azt értjük, hogy log R-nek egy korlátos hatványa (ez a korlát persze függ k0-tól).
Ezt felhasználva a fenti hiba O(R2logO(1)R). Ez valóban elhanyagolható: emlékezzünk vissza, hogy mi olyan főtagot várunk, ami x/logO(1)x nagyságú. Ehhez képest R2logO(1)R csak  , és R=xc/2, ahol c< , és R=xc/2, ahol c<  1. 1.
A továbbiakban a főtagot fogjuk becsülni. (A) célunkat figyelembe véve x-szel osztunk, így elegendő belátni, hogy
![\sum_{d_1,...,d_{k_0},d_1',...,d_{k_0}'} \left(\prod_{j=1}^{k_0}\mu(d_j)\mu(d_j')\right) f\left(\frac{\log d_1}{R},...,\frac{\log d_{k_0}}{R}\right) f\left(\frac{\log d_1'}{R},...,\frac{\log d_{k_0}'}{R}\right)\frac{1}{W[d_1,d_1']\cdot...\cdot[d_{k_0},d_{k_0}']}=(\alpha+o(1))\left(\frac{W}{\varphi(W)}\right)^{k_0} \frac{1}{\log^{k_0}R}.](keplet.cgi?k=538B0CA0908D865C)
|
| Előzmény: [174] Maga Péter, 2013-12-28 17:31:42 |
|
| [175] Maga Péter | 2013-12-29 17:45:22 |
 Erratum: a második hosszú képletben > helyett legyen =.
A végén pedig van egy ilyen: ,,Ekkor minden x-re elkészíthető egy megfelelő 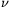 súlyfüggvény f segítségével, ahol (...)'' Ez úgy értendő, hogy ezeket be fogjuk bizonyítani: megadjuk súlyfüggvény f segítségével, ahol (...)'' Ez úgy értendő, hogy ezeket be fogjuk bizonyítani: megadjuk 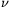 -t, és belátjuk a megadott formulákat. -t, és belátjuk a megadott formulákat.
|
| Előzmény: [174] Maga Péter, 2013-12-28 17:31:42 |
|
| [174] Maga Péter | 2013-12-28 17:31:42 |
 A feladat sokaknak talán túl egyszerű volt ahhoz, hogy billentyűzetet ragadjanak, ezért megoldom én magam. Egyrészt

Alkalmazva az (A) és (B) feltételeket, az előző legalább

Ez pozitív, ha x elég nagy, köszönhetően a (C) feltételnek. Tehát létezik olyan n, amire a belső összeg pozitív, rögzítsünk egy ilyet.
Ekkor

Világos, hogy ha x>hk0, akkor 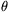 (n+hj)<log (3x), így legalább m+1 darab (n+hj)<log (3x), így legalább m+1 darab 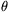 (n+hj)-nek kell pozitívnak lennie. Ez éppen azt jelenti, hogy n+H-ban legalább m+1 prím van. (n+hj)-nek kell pozitívnak lennie. Ez éppen azt jelenti, hogy n+H-ban legalább m+1 prím van.
Az alkalmas súlyfüggvény felé I.
Legyen  a prímek egy megengedett eloszlási szintje, azaz tegyük fel, hogy EH( a prímek egy megengedett eloszlási szintje, azaz tegyük fel, hogy EH( ) fennáll; emlékezzünk vissza, hogy ) fennáll; emlékezzünk vissza, hogy  =1/2-re és kisebbekre ezt tudjuk (Bombieri-Vinogradov), =1/2-re és kisebbekre ezt tudjuk (Bombieri-Vinogradov),  =1-re csak sejtjük (Elliott-Halberstam)! Rögzítsük a 0<c< =1-re csak sejtjük (Elliott-Halberstam)! Rögzítsük a 0<c< valós számot, és legyen R=xc/2. valós számot, és legyen R=xc/2.
Jelöljük  k0-val a következő k0 dimenziós szimplexet: k0-val a következő k0 dimenziós szimplexet:
 k0={(t1,...,tk0):0 k0={(t1,...,tk0):0 tj< tj<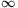 ,t1+...+tk0 ,t1+...+tk0 1}, 1},
tehát azt, ami minden koordinátában a nemnegatív féltérbe esik, és a koordináták összege legfeljebb 1. Tegyük fel, hogy f:[0,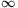 )k0 )k0 R egy olyan függvény, mely sima (deriválható minden változó szerint, a deriváltjai is tovább deriválhatók minden változó szerint, és így tovább) és R egy olyan függvény, mely sima (deriválható minden változó szerint, a deriváltjai is tovább deriválhatók minden változó szerint, és így tovább) és  k0-n kívül 0. k0-n kívül 0.
Ekkor minden x-re elkészíthető egy megfelelő 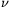 súlyfüggvény f segítségével, ahol súlyfüggvény f segítségével, ahol



Itt  k0-1 a k0-1 a  k0-hoz hasonlóan definiált, eggyel alacsonyabb dimenziós szimplexet jelöli, f1,...,k0 f-nek azt a parciális deriváltját, amikor minden változó szerint egyszer deriválunk, f1,...,k0-1 pedig f-nek azt a parciális deriváltját, amikor az utolsó változó kivételével minden változó szerint egyszer deriválunk. k0-hoz hasonlóan definiált, eggyel alacsonyabb dimenziós szimplexet jelöli, f1,...,k0 f-nek azt a parciális deriváltját, amikor minden változó szerint egyszer deriválunk, f1,...,k0-1 pedig f-nek azt a parciális deriváltját, amikor az utolsó változó kivételével minden változó szerint egyszer deriválunk.
|
| Előzmény: [173] Maga Péter, 2013-12-17 19:12:31 |
|
| [173] Maga Péter | 2013-12-17 19:12:31 |
 Célkitűzés.
Bevezetünk még egy jelölést: 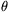 (n)=log n, ha n prím, és legyen (n)=log n, ha n prím, és legyen 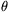 (n)=0 egyébként. Ez a prímhatványokon kívül ugyanaz, mint a (n)=0 egyébként. Ez a prímhatványokon kívül ugyanaz, mint a  . .
Legyen k0 2, m 2, m 1 rögzített. Tegyük fel, hogy valamely fix (csak k0-tól és m-től függő) 1 rögzített. Tegyük fel, hogy valamely fix (csak k0-tól és m-től függő)  , , >0 számokra, minden megengedett k0 elemű H halmazra és minden b modulo W maradékosztályra, melyre b+H minden eleme relatív prím W-hez, található egy olyan >0 számokra, minden megengedett k0 elemű H halmazra és minden b modulo W maradékosztályra, melyre b+H minden eleme relatív prím W-hez, található egy olyan 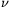 nemnegatív valós értékű súlyfüggvény, valamint R,B>0 (x-től függő) mennyiségek, melyekre teljesülnek a következők. nemnegatív valós értékű súlyfüggvény, valamint R,B>0 (x-től függő) mennyiségek, melyekre teljesülnek a következők.
(A) Felső becslés az összsúlyra:

(B) Alsó becslés arra, hogy a súly mennyire koncentrálódik a prímekre: minden hj H-ra H-ra

(C) A felsorolt mennyiségek között pedig fennáll

Itt o(1) mindig egy olyan mennyiséget jelöl, ami tart a 0-hoz, amint x-tart a végtelenbe. Tehát az (A), (B) úgy értendők, hogy a bal oldali összegek rendre  , illetve , illetve  . .
Hogy mást is engedjek szóhoz jutni:
Feladat. Bizonyítsuk be, hogy ebben az esetben van olyan x n n 2x, melyekre n+H legalább m+1 prímet tartalmaz. 2x, melyekre n+H legalább m+1 prímet tartalmaz.
Segítőlökés. Tekintsük a

összeget. Bizonyítsuk be, hogy ha x elég nagy, akkor ez pozitív, illetve azt, hogy a külső összeg egy tagja csak akkor lehet pozitív, ha n+H-ban legalább m+1 prím van.
Tehát a továbbiakban a cél az, hogy egy megfelelő súlyfüggvényt konstruáljunk.
|
| Előzmény: [172] Maga Péter, 2013-12-16 20:18:31 |
|
| [172] Maga Péter | 2013-12-16 20:18:31 |
 Megengedett halmazok.
Legyen H={h1,...,hk0} pozitív egészek egy fix, k0 elemű halmaza, mely úgy van indexelve, hogy h1<...<hk0. Azt szeretnénk megmutatni, hogy végtelen sok olyan pozitív egész n létezik, melyre n+H={n+h1,...,n+hk0} legalább m+1 darab prímet tartalmaz. Ha m=1, és sikerülne ezt valamilyen fix H-ra megmutatni, akkor az azt jelentené, hogy végtelen sokszor előfordul, hogy két szomszédos prím különbsége legfeljebb k0 (k0=1, h1=2-re ez az ikerprím-sejtés lenne).
Nyilván m+1 k0-nak fenn kell állnia, k0-nál több prím nem fér bele H semelyik eltoltjába sem. Azonban ez nem feltétlen elég. Gondoljunk arra, hogy ha m=2, azaz három prímet keresünk, és H={2,4,6}, akkor biztosan nem igaz, hogy n+H végtelen sok n-re tartalmazna három prímet, hiszen n+H valamelyik eleme osztható 3-mal. k0-nak fenn kell állnia, k0-nál több prím nem fér bele H semelyik eltoltjába sem. Azonban ez nem feltétlen elég. Gondoljunk arra, hogy ha m=2, azaz három prímet keresünk, és H={2,4,6}, akkor biztosan nem igaz, hogy n+H végtelen sok n-re tartalmazna három prímet, hiszen n+H valamelyik eleme osztható 3-mal.
Ezért csak olyan H halmazokkal fogunk dolgozni, melyekkel ilyesmi nem történhet meg, azaz feltesszük, hogy a H halmaz semelyik p prímre sem fedi le az összes maradékosztályt (minden p prímre van olyan a maradékosztály, hogy hj a(p) nem áll fenn egyetlen 1 a(p) nem áll fenn egyetlen 1 j j k0-ra sem). Egy ilyen halmazt megengedettnek nevezünk. k0-ra sem). Egy ilyen halmazt megengedettnek nevezünk.
Néhány további jelölés.
Legyen x egy nagy szám, gondoljunk rá úgy, hogy tart a végtelenbe, és mi az egymáshoz közeli prímeket az [x,2x] intervallumban fogjuk keresni.
Legyen w=[log log log x] ([.] most az alsó egészrész). Legyen továbbá  a prímek szorzata w-ig. a prímek szorzata w-ig.
|
| Előzmény: [168] Maga Péter, 2013-12-15 19:13:52 |
|
|
| [170] Maga Péter | 2013-12-16 09:25:54 |
 Ez a jelölés I. M. Vinogradovtól származik. Néhány alapmű, aminek a bevezetőjében leírják, mit jelent: Iwaniec-Kowalski: Analytic number theory, Davenport: Multiplicative number theory; Montgomery-Vaughan: Multiplicative number theory I. classical theory.
|
| Előzmény: [169] Lóczi Lajos, 2013-12-16 08:21:15 |
|
|
| [168] Maga Péter | 2013-12-15 19:13:52 |
 Az EH( ) hipotézis. ) hipotézis.
Jelöljük  (n)-nel a von Mangoldt függvényt: ha n a p prím (pozitív egész kitevős) hatványa, akkor (n)-nel a von Mangoldt függvényt: ha n a p prím (pozitív egész kitevős) hatványa, akkor  (n)=log p, minden egyéb esetben (n)=log p, minden egyéb esetben  (n)=0. A prímszámtétel egy lehetséges megfogalmazása, hogy (n)=0. A prímszámtétel egy lehetséges megfogalmazása, hogy

(Mivel nem prím prímhatványból kevés van, ezért ez ekvivalens azzal, hogy x-ig a prímek logaritmusának összege körülbelül x.)
A korlátos hézagokra vonatkozó tételekben szükségünk van valamilyen kontrollra a prímek maradékosztályok közötti eloszlása felett. Dirichlet klasszikus tétele értelmében minden a modulushoz relatív prím (redukált) maradékosztályban vannak prímek. Ennél több is igaz, nevezetesen az, hogy a prímek a redukált maradékosztályok között egyenletesen oszlanak el. Hogy mennyire egyenletesen, azt a következő fogalommal kívánjuk mérni.
Azt mondjuk, hogy a  a prímek egy megengedett eloszlási szintje, ha minden A>0 (erre gondoljunk úgy, hogy nagy) és minden a prímek egy megengedett eloszlási szintje, ha minden A>0 (erre gondoljunk úgy, hogy nagy) és minden  >0 (erre gondoljunk úgy, hogy pici) számra >0 (erre gondoljunk úgy, hogy pici) számra

[Az itt megjelenő  jelölés azt jelenti, hogy létezik olyan A-tól és jelölés azt jelenti, hogy létezik olyan A-tól és  -tól függő C konstans, hogy a 'bal oldal' <C 'jobb oldal'; -tól függő C konstans, hogy a 'bal oldal' <C 'jobb oldal';  (q) a q-hoz relatív prím maradékosztályok száma.] (q) a q-hoz relatív prím maradékosztályok száma.]
Tehát ha minden q modulus esetében kiválasztjuk azt a maradékosztályt, amelyikben a prímek száma (illetve az ezeket imitáló  -értékek összege) legjobban eltér az átlagostól, és ezeket összeadjuk, amint q-val felmegyünk egészen -értékek összege) legjobban eltér az átlagostól, és ezeket összeadjuk, amint q-val felmegyünk egészen  -ig, még az így kapott átlagostól való legnagyobb eltérések összege sem túl nagy (ahhoz hasonlítva, hogy mennyi a -ig, még az így kapott átlagostól való legnagyobb eltérések összege sem túl nagy (ahhoz hasonlítva, hogy mennyi a  -k összege x-ig): x/(akármekkora log x-hatvány). -k összege x-ig): x/(akármekkora log x-hatvány).
Mekkora lehet a prímek egy megengedett eloszlási szintje? Könnyű látni, hogy  >1-et nem írhatunk: ha q mondjuk x/2 és x között végigfut, akkor az átlagostól való eltérés minden egyes q-ra legalább log x konstansszorosa, ez x/2 darab q-ra már legalább konstansszor xlog x nagyságú. Ugyanakkor triviálisan a 0 megengedett eloszlási szint. Triviális továbbá, hogy ha egy pozitív szám megengedett eloszlási szint, akkor minden nála kisebb szám is az. Előző kérdésünk tehát arra redukálódik, hogy mekkora a prímek legnagyobb megengedett eloszlási szintje. >1-et nem írhatunk: ha q mondjuk x/2 és x között végigfut, akkor az átlagostól való eltérés minden egyes q-ra legalább log x konstansszorosa, ez x/2 darab q-ra már legalább konstansszor xlog x nagyságú. Ugyanakkor triviálisan a 0 megengedett eloszlási szint. Triviális továbbá, hogy ha egy pozitív szám megengedett eloszlási szint, akkor minden nála kisebb szám is az. Előző kérdésünk tehát arra redukálódik, hogy mekkora a prímek legnagyobb megengedett eloszlási szintje.
Elliott-Halberstam-sejtés:  =1 megengedett eloszlási szint. Ez egy sejtés, nem tudjuk, hogy igaz-e. =1 megengedett eloszlási szint. Ez egy sejtés, nem tudjuk, hogy igaz-e.
Bombieri-Vinogradov-tétel:  =1/2 megengedett eloszlási szint. Ez egy tétel, a múlt század 60-as éveiben bizonyították be. =1/2 megengedett eloszlási szint. Ez egy tétel, a múlt század 60-as éveiben bizonyították be.
Most egy jó darabig csak annyit fogunk használni, hogy létezik olyan  >0, ami megengedett eloszlási szint, konkrét esetben >0, ami megengedett eloszlási szint, konkrét esetben  =1/2-et is odaképzelhetünk, illetve fantáziálhatunk arról, hogy =1/2-et is odaképzelhetünk, illetve fantáziálhatunk arról, hogy  =1 mennyivel erősebb eredményt adna. =1 mennyivel erősebb eredményt adna.
|
|
| [167] Maga Péter | 2013-12-13 20:38:04 |
 Néhány évvel ezelőtt, azt hiszem, a fórum több olvasója számára is mulatságosak voltak az elemi próbálkozások az ikerprím-sejtés bizonyítására. 2013 májusa óta azonban nagy változások történtek a számelméletben.
Már az a tény is egészen megdöbbentő, hogy a 'korlátos hézagokat' sikerült igazolni. Több az annál, a 'korlátos intervallumokat' nemcsak két, hanem akárhány prímre is sikerült igazolni.
Még jobban meglepődtem, amikor Tao blogbejegyzését olvastam. Ugyanis ez a bizonyítás - ha nem is egészen elemi - igazán mély számelméleti ismeretek nélkül is megérthető. Amennyiben a fórum olvasói közül néhányaknak megvan hozzá a kedve, akkor ajánlom itteni feldolgozásra (és ebben közreműködésemet is felajánlom). Nos?
|
|
|
| [165] Maga Péter | 2013-10-30 10:19:22 |
 ,,Már csak (...) és kész a sejtés.''
A jelenlegi módszer a Goldston-Pintz-Yildirim szitán alapszik. Ennek elméleti határa 16: ha az Elliott-Halberstam-sejtés igaz, akkor a GPY azt adja, hogy pn-pn-1 16 végtelen sokszor. 16 végtelen sokszor.
|
| Előzmény: [161] Lóczi Lajos, 2013-10-29 18:07:50 |
|
| [164] Maga Péter | 2013-10-30 09:55:03 |
 Ez tényleg nagyon jó hír. Magyar vonatkozásban meg kell említeni Pintz Jánost is (nagyon fontos szerepe van ezekben az eredményekben), aki éppen mostanában tart egy előadássorozatot a Rényiben korlátos hézagokról.
|
| Előzmény: [162] Lóczi Lajos, 2013-10-29 18:12:16 |
|
| [163] Maga Péter | 2013-10-30 09:50:08 |
 Valójában már sokkal jobban állunk, érdemesebb ezt nézni (vagy Tao blogjának frissebb bejegyzéseit és a kommenteket).
Ha jól látom, a jelenlegi legjobb ellenőrzött 4680. Érdekes Maynard bejelentése 700 körüli különbséggel, de ez még megerősítést vár.
|
| Előzmény: [161] Lóczi Lajos, 2013-10-29 18:07:50 |
|
|
|
|
|
