| [1951] gyula60 | 2024-08-30 17:09:29 |
 A húrnégyszögekkel kapcsolatos megjegyzéseket szeretnék most leírni. 1./Van a húrnégyszögeknek egy triviális tulajdonsága, amelyről nem látok semmit se a KÖMAL-on, sem a Wikipédián. (Lehet, hogy figyelmetlen vagyok.) Nevezetesen hogy a húrnégyszög oldalaiból még két húrnégyszög is konstruálható. Összesen három (igaz az eredetivel se nem hasonló, se nem egybevágó) azonos területű és kerületű húrnégyszög jöhet szóba összesen e, f és g átlókkal. A keletkező harmadik átló hosszára g2=(ab+cd)(ad+bc)(ac+bd). Ezt felhasználva kikövetkeztethető, hogy T=efg4R. 2./A spanyol nyelvű változatban látható, hogy cosA=a2+d2−b2−c22(ad+bc), ami a koszinusz-tételre emlékeztet. Az angol nyelvű változat T=(ad+bc)sinA2 és T=(ab+cd)sinB2 képletei pedig arra engednek következtetni, hogy a szomszédos szögek szinuszainak aránya az átlók arányával egyezne meg, ami pedig a szinusz-tételre hasonlít.
|
|
|
| [1949] Sinobi | 2022-01-20 17:35:41 |
 Szerintem ezt a kérdést megválaszoltam [1940]-ben, mekkorák az A és B-beli szögek.
A B-beli szög 64.34, az
A-beli szög 51.32.
Az ábrádat nem látom jól, de ha a 0 fok van jobb oldalt, és az alsó kör óramutatóval megegyezően, a felső pedig ellentétesen van számozva (???), akkor a metszéspontok az alsó körön
270 +- A-beli szög = 270 +- 51.32 = 321.32 és 218.68,
míg a felső körön
90 +- B-beli szög = 90 +- 64.34 = 154.34 és 25.66.
|
| Előzmény: [1947] HappyEffendi, 2022-01-19 20:34:48 |
|
| [1948] HappyEffendi | 2022-01-19 22:54:38 |
 Amint 1943-as hsz-ben jeleztem közreadnám a következő feladatot:
Adott egy 'r' sugarú kör, és annak ívén levő középponttal 6 db 'gyök(3)*r/2' sugarú kör.
Mekkora a 12 fehér köríves vonallal határolt alakzat területe?
|
 |
|
| [1947] HappyEffendi | 2022-01-19 20:34:48 |
 Kedves Erzsébet!
Köszönöm, hogy foglalkozol a témával!
Megpróbálom még szakszerűbben leírni a feladatot:
Adott két kör. A nagyobbik sugara 'r', a kisebbiké 'gyök(3)*r/2'. A kisebbik kör középpontja a nagyobbik 270. fokán van. 1943-as hozzászólás ábrája szerint.
A feladat: középpontjaiktól számítva egy-egy teljes körív mentén, hány foknál vannak a metszéspontjaik?
|
| Előzmény: [1946] Berko Erzsebet, 2022-01-17 16:58:15 |
|
| [1946] Berko Erzsebet | 2022-01-17 16:58:15 |
 Sajnos a pontos feladatot nem írtad. Adott két kör. Ha a metszéspontot összekötöm a körök középpontjával, akkor a szög: 64,34 fok. VAGY Két görbe hajlásszöge: metszéspontban húzott érintők által bezárt szög. Ez is 64,34 fok.
|
| Előzmény: [1945] HappyEffendi, 2022-01-16 23:46:29 |
|
|
|
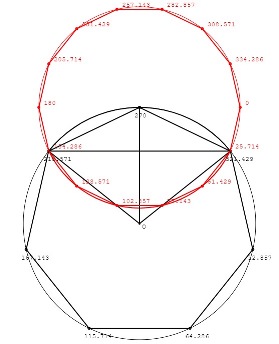
| [1943] HappyEffendi | 2022-01-06 14:41:58 |
 Kedves Sinobi!
Boldog Újévet Kívánok (természetesen mindenki másnak is)!
Sejtettem, hogy szakszerűtlen lesz a feladat leírása, de a segítségeddel mégis sikerült elindulnom a megoldás felé, főleg, miután rájöttem, hol keressem az egyenlőszárú háromszöget. :)
Az alap kérdésem az lett volna, hogy egy-egy körnek hányadik fokainál vannak a másik körrel való metszéspontjai?
Szerkesztés közben arra is rájöttem, hogy a két kör metszéspontjai egy, a nagy körbe írható szabályos hétszög, és egy, a kis körbe írható szabályos tizennégy-szög egy-egy csúcsánál vannak.
Gondolom, a geometriában képzettek ezt kapásból tudtják.
A metszéspontok e szerint:
a kis körnél 25,714 és 154,286 fok,
a nagy körnél 218,571 és 321,429 fok,
az alábbi ábra szerint.
A fenti kérdés egy összetettebb feladat része volt, amivel, ha sikerül ábrázolnom, ismét jelentkezem.
Köszönöm segítségeteket!
|
 |
| Előzmény: [1941] Sinobi, 2021-12-31 10:11:02 |
|
| [1942] Berko Erzsebet | 2022-01-02 08:13:12 |
 Szerintem először le kellene írni a feladatot, vagyis pontosítani kellene. Metszéspontok szöge? Mivel ez számomra nem világos, én pl. a két érintő szögére gondoltam.
Két metsző kör szögén a metszéspontban meghúzott körérintők szögét értjük.
|
|
| [1941] Sinobi | 2021-12-31 10:11:02 |
 Mármint a szög arccos( (piros/2) / kék ), ahol a piros gyök(3)/2, a kék pedig 1.
|
|
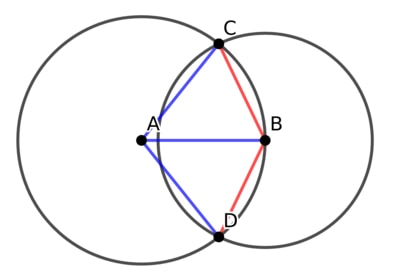
| [1940] Sinobi | 2021-12-31 10:02:11 |
 Úgy értelmeztem a kérdésedet, hogy a körívek által bezárt szögre vagy kíváncsi (ábrán az ABC háromszög C-ben levő szöge). Most inkább úgy hiszem, hogy az ábrán az ABC háromszögben A-ban, illetve B-ben levő szögekre (vagy azok duplájára) vagy kíváncsi.
Akárhogy is, a háromszög oldalai (r, r, sqrt(3)/2 r), aminek az alapon fekvő szögei (C és B-beli szögek) arcos( kék/ (piros/2) ) = arccos( gyök(3) / 2 / 2), az A-beli szöge meg 180-2*arccos( gyök(3) / 4)).
|
 |
| Előzmény: [1939] HappyEffendi, 2021-12-30 20:31:56 |
|
|
| [1938] Sinobi | 2021-12-30 15:21:39 |
 Körök szöge az ugyanaz, mint a metszéspontba húzott sugarak szöge.
Ha felveszed a középpontokat és a metszéspontba húzott sugarakat, akkor egy (r,r,gyök(3)/2 r) egyenlőszárú háromszöget kapsz, és ennek a szögeire vagy kíváncsi.
|
| Előzmény: [1936] HappyEffendi, 2021-12-27 23:49:47 |
|
| [1937] HappyEffendi | 2021-12-28 00:14:23 |
 Elnézést, az ábra lemaradt, de talán nincs is rá szükség!
|
 |
|
| [1936] HappyEffendi | 2021-12-27 23:49:47 |
 Kedves Fórumozók!
Segítséget kérnék, mivel nem vagyok járatos a matematika és geometria világában:
Adott két egymást metsző kör. Az egyik r, a másik négyzetgyök(3) * r / 2 sugarú. A nagyobbik kör érinti a kisebbik középpontját.
Kérdésem: mi a képlet a metszéspontok szögeinek meghatározásához?
JavaScript-ben rajzoltam meg canvas-on, szemre többé-kevésbé jól kidekáztam az értékeket, de jó lenne, ha a gép pontosan kiszámolná. A teljesség kedvéért ideírom a körívrajzolás kódját:
ctx.arc(x, y, r, (Math.PI / 180) * 218.65, (Math.PI / 180) * 321.35);// nagy kör íve, ctx.arc(x, y, Math.sqrt(3) * r / 2, (Math.PI / 180) * 25.65, (Math.PI / 180) * 154.35);// kis kör íve, az óramutató járása szerint.
Bocsánat a valószínűleg szakszerűtlen feladatleírásért és előre is köszönök minden segítséget!
|
|
|
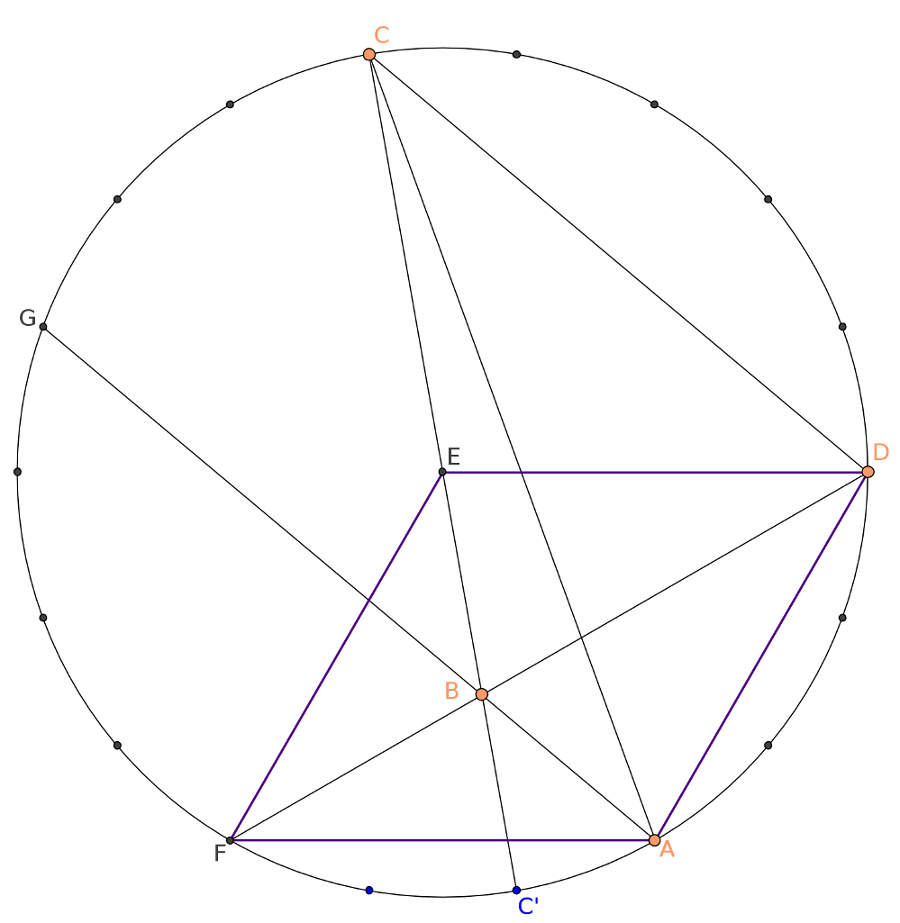
| [1934] Erben Péter | 2021-06-07 14:39:58 |
 A feladat egy lehetseges eredete a szabalyos 18-szog atloinak az a tulajdonsaga, hogy egymassal bezart szoguk mindig a 10 fok egesz tobbszorose.
Ha C, D es A egy szabalyos 18-szog megfelelo csucsai, akkor E eppen a sokszog kozeppontja.
A kozbulso lepes, hogy a CC′, AG es DF atlok egy ponton mennek at, ami peldaul visszavezetheto arra, hogy EDAF egy rombusz, amelynek szogei 120 fok es 60 fok.
Mindez persze nem a feladat megoldasa, inkabb azt mutatja, hogyan "keszulhetett" a kerdes.
|
 |
| Előzmény: [1933] Lpont, 2021-06-07 12:32:53 |
|
| [1933] Lpont | 2021-06-07 12:32:53 |
 I. Szögszámolással adódik, hogy BD felezi az ABCD négyszög B-nél levő szögét.
II. A-t tükrözve BD-re a kapott E pont rajta van BC egyenesén és AD=ED.
III. Újabb szögszámolás után EDC háromszög egyenlő szárú, ED=EC.
IV. Harmadjára is szögeket számolva EC=EA, tehát AE=EC=ED=AD, azaz AED háromszög szabályos, minden szöge 6alfa, így alfa=10fok.
|
| Előzmény: [1932] rezes, 2021-06-06 13:18:23 |
|
| [1932] rezes | 2021-06-06 13:18:23 |
 ABCD konvex négyszögben BC=CD,BAC∢=3α, BCA∢=α, ACD∢=3α, DAC∢=5α. Mennyi α értéke?
|
|
|
| [1930] HoA | 2021-02-03 12:34:31 |
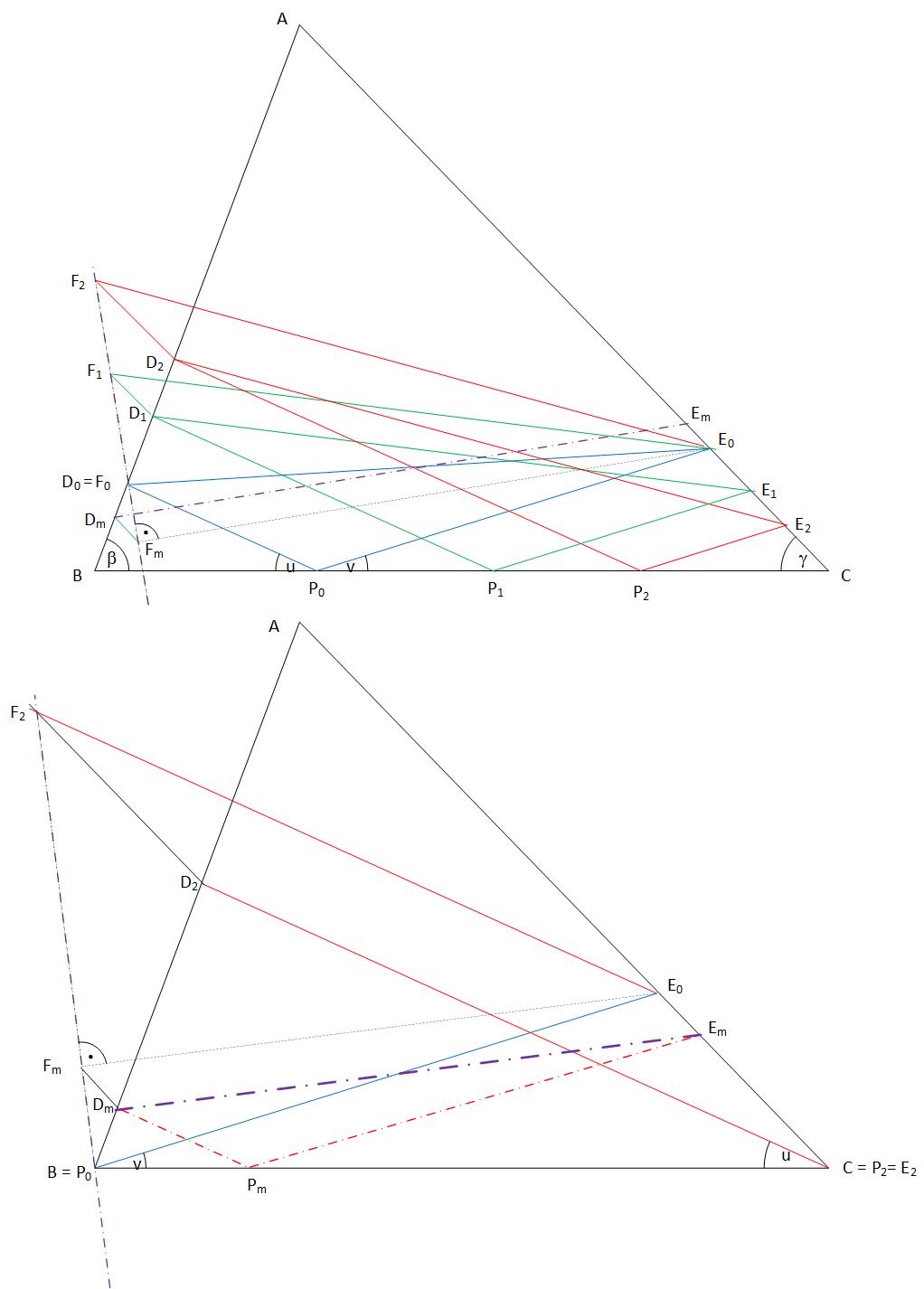
 Legyen P egyik helyzete P0. Rajzoljuk meg az ehhez tartozó P0D0 és P0E0 szakaszokat. P egy másik, P1 helyzetéhez tartozzanak A D1 és E1 pontok. A párhuzamos szelők tétele szerint BP0D0 háromszögből D0D1=kP0P1 , ahol k=sinusin(β+u) . Hasonlóan a P0CE0 háromszögből E0E1=mP0P1 , ahol m=sinvsin(γ+v) . Toljuk el E1D1 -et önmagával párhuzamosan az AC egyenes mentén úgy, hogy E1 E0 -ba kerüljön. D1 új helyzete legyen F1 . D1E1E0F1 paralelogramma, D1F1#E1E0 , D0D1D1F1=km. Ismételjük meg egy további P2 pontra a P1 -re elvégzetteket. Kapjuk a D2,E2,F2 pontokat. D0D2D2F2=km. A D0D1F1 és D0D2F2 háromszögek hasonlók, D0,D1ésD2 egy egyenesen vannak. A megfelelő DiEi szakasszal párhuzamos és azonos hosszúságú FiE0 szakaszok egyik végpontja közös (E0) , a másik az FiFj egyenesen mozog. Közülük a legrövidebb az E0 -ból az FiFj -re bocsátott merőleges Fm talppontját E0 -lal összekötő szaksz lesz. A keresett legrövidebb DE szakaszt akkor kapjuk, ha E0Fm -et az AC egyenes mentén úgy toljuk el, hogy Fm az AB egyenesre essék, a szakasz végpontjai legyenek DmésEm
A szerkesztést úgy hajthatjuk végre a legkevesebb vonal megrajzolásával, ha P két szélső helyzetét használjuk. Legyen tehát P0=B,P2=C , E0 az AC oldalnak az a pontja, melyre E0BC∠=v , D2 az AB oldalnak az a pontja, melyre D2CB∠=u . CD2 -t CA mentén úgy eltolva, hogy C E0 -ba jusson D2 kerüljün F2 -be .E0 -ból az F2B egyenesre bocsátott merőleges talppontja legyen Fm . A legrövidebb DE szakaszt E0Fm -nek AC -vel párhuzamos eltolásával kapjuk úgy, hogy Fm az AB egyenesen lévő Dm -be kerüljön, E0 pedig Em -be.
Ujjgyakorlatnak hagyjuk annak bizonyítását, hogy a Dm -ből D2C -vel húzott párhuzamos és az Em -ből E0B vel húzott párhuzamos egy, a BC egyenesen fekvő, feladatunk megoldását adó Pm pontban metszik egymást.
|
 |
| Előzmény: [1929] sakkmath, 2021-01-21 23:58:57 |
|
| [1929] sakkmath | 2021-01-21 23:58:57 |
 A 192. feladat valóban nyitott. Talán ezért (is) nagyon nehéz, de megoldható. Az általam ismert megoldást nyolc éve publikálták, azóta a közlés helyén, egy közismert, frekventált oldalon, állócsillagként ragyog: még nem reagált rá senki – legalábbis ott nem. Ebből arra következtetek, hogy máig csak ez az egy megoldás létezik. Ez a dolgozat – a szerkesztéses részét tekintve – mindvégig euklideszi szerkesztésekkel jut el a P pont keresett pozíciójához.
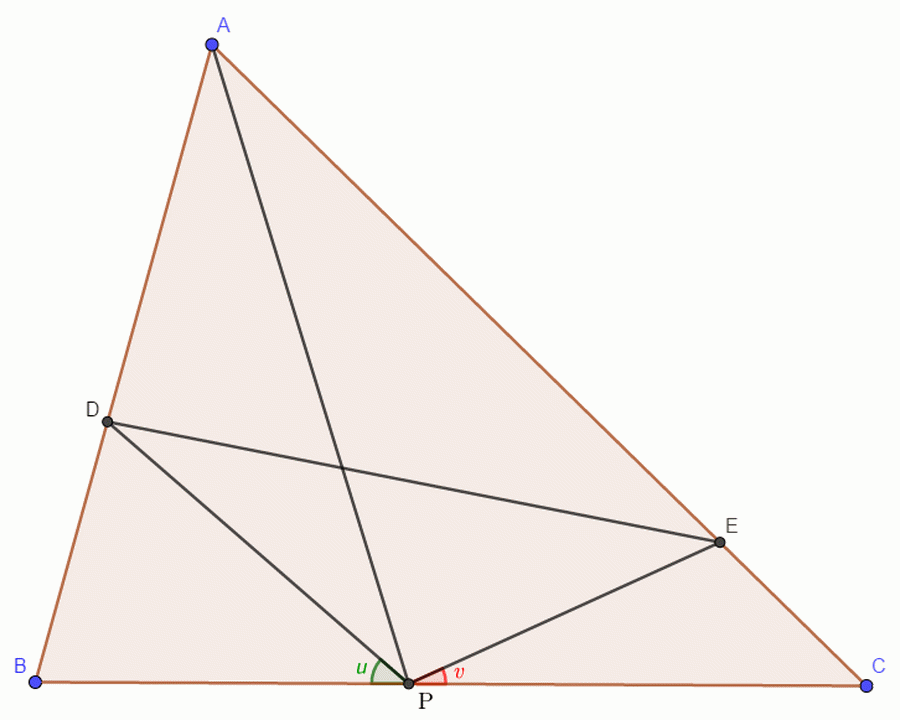
Beírom a lényegesen könnyebb,193. feladatot is, amely csak u és v szerepét tekintve különbözik a rokon 192.-től. Találjunk euklideszi szerkesztést alkalmazó megoldást a következő, 193. feladatra:
Az ABC háromszög BC oldalán mozog egy P pont. Az AB oldal D, valamint az AC oldal E pontjára fennáll, hogy rögzített e két szög: u=BPD∠ és v=CPE∠. Keressük meg a P pont azon helyzetét, amelyre a DE szakasz hossza minimális!
|
 |
| Előzmény: [1928] Sinobi, 2021-01-19 18:24:05 |
|
| [1928] Sinobi | 2021-01-19 18:24:05 |
 Nagyon nyitott a feladat, és nekem kételyeim is vannak azzal kapcsolatban, hogy van értelmes, szép válasz. Az ennél egyszerűbbnek tűnő
Philo szelő probléma: adott egy szög és benne egy pont, keressük meg a legrövidebb szakaszt, amely átmegy a ponton, és a végpontjai a szög két szárán van
sem szerkeszthető már körzővel és vonalzóval. Bár az például megoldható olyan eszközzel, amelyik megadja két kúpszelet metszéspontjait.
|
|
| [1927] sakkmath | 2021-01-13 23:43:55 |
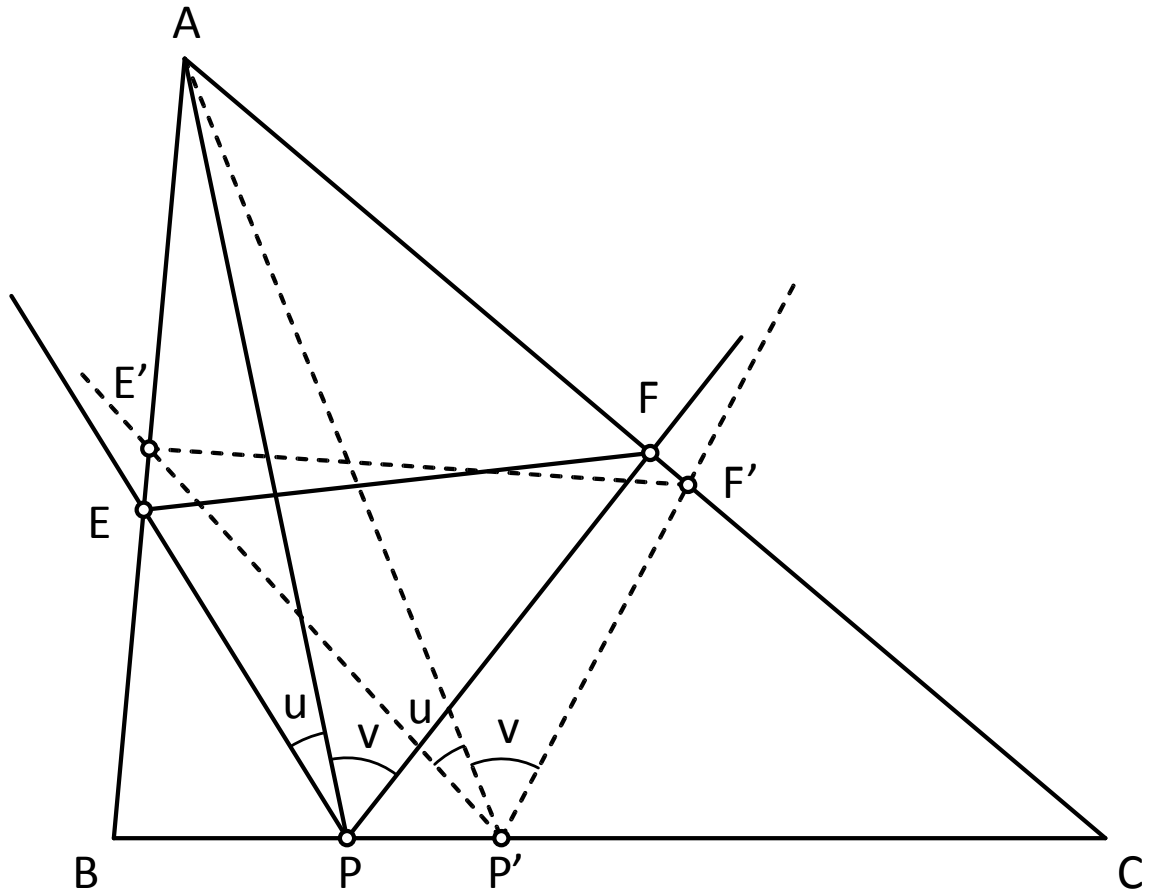
 192. feladat: Az ABC háromszög BC oldalán mozog egy P pont. Az AB oldal E, valamint az AC oldal F pontjára fennáll, hogy konstans az u=EPA∠ és a v=APF∠. Keressük meg a P pont azon helyzetét, amelyre az EF szakasz hossza minimális!
|
 |
|















