Fórum: Valaki mondja meg!

Igazoljuk, hogy a $\displaystyle \rm{sin}(n^2)$ sorozatnak tetszőleges -1-nél nem kisebb és +1-nél nem nagyobb szám lehet torlódási pontja.

Tekintsük a $\displaystyle \rm{sin}(5n^2+3n*i)$ sorozatot, ahol $\displaystyle i^2=-1$ Milyen komplex számok lehetnek ennek a sorozatnak a torlódási pontjai? Előre is köszönöm mindenki segítségét.

Biztos, hogy 3-4 centiméter és nem milliméter a vastagság? Ez így már tényleg köbméter körüli nagyságrend, és tényleg kb. 50 zsák jön ki.

Érdemes lehet mindent valami barátságosabb mértékegységbe átváltani, mondjuk literbe. Az anyag megadott tömege $\displaystyle 1,6\,\mathrm{kg/nm/mm}$. Ez a $\displaystyle \mathrm{m}^2\cdot\mathrm{mm}$ éppen egy liter. A $\displaystyle 1,6\,\mathrm{kg/liter}$ sűrűség hihetőnek tűnik.

Kicsit kerekítve, ha egy $\displaystyle 5\mathrm{m}\times 5\mathrm{m}$-es területet szeretnél $\displaystyle 3\mathrm{cm}$ vastagon bekenni, az $\displaystyle 5\times5\times0,03=0,75$ köbméter, vagyis $\displaystyle 750$ liter. Ehhez kb. $\displaystyle 1200\mathrm{kg}$, vagis kb. $\displaystyle 50$ zsák padlókiegyenlítőre van szükség.

→ aljzatkiegyenlítő kalkulátor

Segítséget szeretnék kérni, hogy mennyi padlókiegyenlítőre, hány zsákra lesz szükségem? A szoba 510x470 cm alapterületű. Felrajzoltam egy méterszer méteres hálót, és a csomópontokban lézerrel kimértem a legmagasabb ponthoz képest a magasságokat. Így a következő magasságpontokat kaptam centiméterben az egyes rácspontokra, ahol a p első indexe az x tengely koordinátáját jelöli, a második index jegy pedig az y koordinátáját:

p00=1,5 (cm)

p10=2,5

p20=2,5

p30=2

p40=1

p50=0,5

p01=2

p11=3

p21=3

p31=3

p41=3

p51=3

p02=2

p12=4

p22=5

p32=4,5

p42=3,5

p52=3,5

p03=2,5

p13=3,5

p23=3

p33=4

p43=4

p53=2

p04=1

p14=3

p24=3,5

p34=4

p44=4

p54=4

p05=0

p15=1

p25=3

p35=3,5

p45=2,5

p55=4,5

Ha számít, akkor ebben a koordináta rendszerben a szoba rövidebb oldala (470 cm) az x tengelyen van, a hosszabbik (510 cm) az y tengelyen.

Az 510*470 cm-es szoba padlója, fala és a különböző magasságú rácspontokból alkotott felület által határolt testnek a térfogatát keresem.

Illetve utána az általam használt padlókiegyenlítő olyan, hogy 1,6 kg/nm/mm és egy zsák 25 kg.

A kérdés, hogy hány zsák szükséges egészre kerekítve? Nekem 61 jött ki a következő számolással.

Egy-egy méteres négyzet alaphoz vettem a hozzá tartozó 4 magasságot, összeadtam őket és osztottam néggyel. Vagyis vettem a különböző magasságok számtani közepét, mint átlagos magasság és szoroztam az alappal, ami 1.

50 zsák kb. 200e Ft és ez a legolcsóbb anyag, amit lehet kapni, szóval nagyon fontos, hogy jó legyen a nagyságrend.

Valóban, köszi! :-)

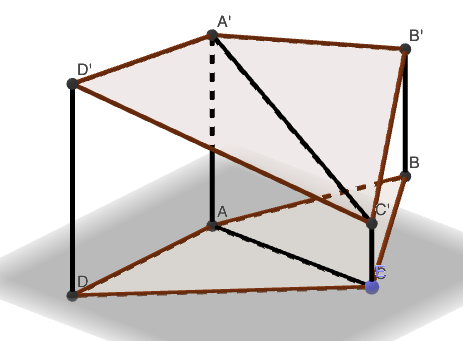
Mar negyszogre sem igaz. Nezzuk az alabbi testet:

$\displaystyle (A(1, 0, 0), B(0, -3, 0), C(-2, 0, 0), D(1, 3, 0)$

$\displaystyle A'(1, 0, 3), B'(0, -3, 2), C'(-2, 0, 1), D'(1, 3, 10/3))$

Ekkor az $\displaystyle ABC$ es $\displaystyle ADC$ haromszogek terulete megegyezik, legyen ez $\displaystyle t$, ekkor a teljes terfogat

$\displaystyle \frac{3+2+1}{3}t+\frac{3+1+10/3}{3}t\neq \frac{3+2+1+10/3}{4}\cdot2t$

Vajon tetszőleges sokszög alap esetén is igaz ez?

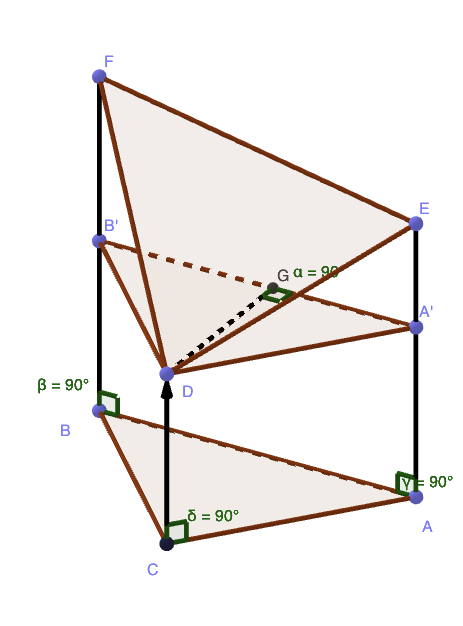
Vagjuk szet egy gulara (vagy tetraederre) es egy egyenes hasabra (parhuzamos alapokkal), innet meg kb. atrendezessel adodik ez.

$\displaystyle V_{hasab}=CD\cdot\frac{DG\cdot AB}{2}=\frac{AA'+CD+BB'}{3}\cdot\frac{DG\cdot AB}{2}$

$\displaystyle V_{gula}=\frac{EA'+FB'}{2}\cdot AB\cdot\frac{GD}{3}$

Tényleg nagyon szépen köszönöm az eddigi segítségeket mindenkinek, nagyon tanulságosak számomra. Eddigi segítségeket tanítás során nagy segítségemre voltak. Most is van egy állítás, amit egyszerűen kellene megindokolni:

Adott egy háromszög alapú egyenes hasáb. A hasáb fedőlapja nem feltétlenül párhuzamos az alaplapjával, de az oldalélek merőlegesek a hasáb alaplapjára. Ekkor a hasáb térfogata egyenlő a hasáb alaplapjának területének és a hasáb oldaléleinek átlagának szorzatával. Előre is köszönök minden segítséget.

1.kérdés

Gondolom a kérdés a $\displaystyle \mod n$ redukált maradékosztályok csoportjára vonatkozik, mert ott szokás primitív gyökről beszélni. Ismert, hogy primitív gyök $\displaystyle \mod n$ $\displaystyle n=2,4$, $\displaystyle n=p^\alpha$, $\displaystyle n=2p^\alpha$ ( p>2 prím) esetén létezik.

Ha n=2, akkor csak az 1 primitív gyök és $\displaystyle 1\cdot1=1$ miatt igaz az állítás.

Ha n=4, akkor csak a 3 primív gyök, de $\displaystyle 3\cdot3=1$ miatt nem igaz az állítás

Ha p>2 prím, akkor a csoport rendjére $\displaystyle \varphi(n)=\varphi(p^\alpha)$ vagy $\displaystyle \varphi(n)=\varphi(2p^\alpha)$ teljesül, ami mindkét esetben páros. De ha $\displaystyle g$ primitív gyök, akkor $\displaystyle g^k$ (k pozitív egész) pontosan akkor lehet primítív gyök, ha $\displaystyle (k,\varphi(n))=1$. Tehát k csak páratlan lehet. Így két primítív gyök szorzata $\displaystyle g$ páros kitevős hatványa, ami viszont nem relatív prím $\displaystyle \varphi(n)$-hez, így nem lehet primitív gyök.

Egyébként a fenti gondolatmenet átvihető tetszőleges 2-nél nagyobb páros rendű ciklikus csoportra ti. két generáló elem szorzata nem generáló elem. Páratlan rendű ciklikus csoportban igaz lehet az állítás, pld ha $\displaystyle a$ generáló elem, $\displaystyle a\cdot a=a^2$ is generáló elem.

2-ik kerdesre: Ebben az 5.15 es 5.16.-os tetel es az $\displaystyle a_n=2^{-\lfloor n/2\rfloor}$ sorozat (angol wikipedia gyokkriteriumos oldalarol szedve, mert lusta vagyok gondolkodni :) ).

A következő kérdések megválaszolásaban kérek segítséget:

-Lehet-e egy csoportban két primitív gyök szorzata primitív gyök?

-Van-e olyan sor, amelyről hányadoskritériummal el lehet dönteni, hogy konvergens vagy divergens, de gyökkritériummal nem lehet eldönteni? Van-e olyan sor, amelyről gyökkritériummal el lehet dönteni, hogy konvergens vagy divergens, de hányadoskritériummal nem lehet eldönteni?

Előre is köszönök minden segítséget.

jav:

> akkor C kétoldali mellékosztályai egyrétűen kiparkettázzák

Helyett: akkor C $\displaystyle a'_i C b'_j$ alakú kétoldali mellékosztályai egyrétűen kiparkettázzák

2. Legyen inkább $\displaystyle A,B \leq G$, és $\displaystyle C = A \cap B$, és akkor nem kell alsóindexezni.

A feladat valami olyasmit mond, hogy ha $\displaystyle A, B \leq G$, akkor ha $\displaystyle A B = \{a_ib_j\}_{i,j}$-ben elemek egybeesnek, akkor az látszik már $\displaystyle A \cap B$-ben is. Egy szép álom, hogy ha naivan megszámolod $\displaystyle A B$ elemeit, akkor mindent $\displaystyle |A \cap B|$-szer számolsz. Gondolok itt: legyen $\displaystyle a_1 b_1 \in AB$ rögzített, hány $\displaystyle a_2 b_2$ van, hogy $\displaystyle a_1 b_1 = a_2 b_2$? Mivel $\displaystyle {a_2}^{-1}a_1 = b_2{b_1}^{-1} \in C$, eleve maximum C darab $\displaystyle a_2$ jön szóba..

.. egy másik megközelítés, hogy ha $\displaystyle A'$ a $\displaystyle C \leq A$ mellékosztályainak reprezentánsaiból áll, $\displaystyle |A'| = |A|/|C|$, hasonlóan $\displaystyle B'$, akkor $\displaystyle C$ kétoldali mellékosztályai egyrétűen kiparkettázzák $\displaystyle A B$-t. Azt könnyű látni, hogy $\displaystyle AB = A' C B'$ : tartalmazzák egymást. És akkor azt kell belátni hogy két ilyen kétoldali mellékosztály nem esik egybe egyáltalán: $\displaystyle a'_1 c_1 b'_1 = a'_2 c_2 b'_2$ nem lehet. Az meg nem nehéz, hogy $\displaystyle {a'_2}^{-1}a'_1$ pontosan akkor $\displaystyle C$-beli, ha $\displaystyle a'_1 C = a'_2 C$, azaz ugyanazt a mellékosztályt reprezentálják. Ebből a megoldásból nem látszik, hogy $\displaystyle AB$ összeesik, vagy bármi ilyesmi.

1-re:

Ha a K részhalmaz a $\displaystyle H\subseteq G$ részcsoport bal oldali mellékosztálya és $\displaystyle g\in K$ egy rögzített reprezentáns elem, akkor a feltétel szerint $\displaystyle gH=K$.

Legyen $\displaystyle H'=\{ghg^{-1}: h\in H\}$.

Azt állítjuk, hogy $\displaystyle H'$ részcsoportja G-nek és $\displaystyle H'g=K$, azaz K egy jobboldali mellékosztály H'-re.

1. H' zárt a szorzásra, mert tetszőleges $\displaystyle h_1,h_2\in H$ esetén

$\displaystyle (gh_1g^{-1})(gh_2g^{-1})=g(h_1h_2)g^{-1}\in H'$

2. G "e" egységeleme benn van H'-ben, mert $\displaystyle e\in H$ miatt

$\displaystyle e=geg^{-1} \in H'$

3. H' minden elemének inverze H'-beli, mert tetszőleges $\displaystyle h\in H$ esetén

$\displaystyle (ghg^{-1})^{-1}=(g^{-1})^{-1}h^{-1}g^{-1}=gh^{-1}g^{-1} \in H'$

1.-3. miatt H' részcsoport és |H'|=|H| miatt a H'-höz tartozó minden jobboldali mellékosztály elemszáma megegyezik a H-hoz tartozó baloldali mellékosztályok elemszámával, azaz |K|-val. Végül a $\displaystyle H'g$ jobboldali mellékosztály minden elemére $\displaystyle (ghg^{-1})g=gh \in K$, azaz $\displaystyle H'g=K$

3.-ra, ha $\displaystyle G_1=H_1\setminus H_2$ es $\displaystyle G_2=H_2\setminus H_1$ egyszerre nem uresek, akkor $\displaystyle u\in G_1$ es $\displaystyle v\in G_2$ eseten $\displaystyle u^{-1}\in{H_1}$ es $\displaystyle v^{-1}\in H_2$, ekkor $\displaystyle uv$ nem lehet sem $\displaystyle H_1$-ben sem $\displaystyle H_2$-ben, figyelembe veve, hogy $\displaystyle u=(uv)v^{-1}$ es $\displaystyle v=u^{-1}(uv)$

A következő feladatok megoldásában kérek segítséget:

1. Iagzolja, hogy a $\displaystyle G$ csoport valamely $\displaystyle K$ részhalmaza a $\displaystyle G$ csoport valamelyik részcsoportjának bal oldali mellékosztálya, akkor $\displaystyle G$-nek van olyan részcsoportja, amelynek ez a $\displaystyle K$ jobb oldali mellékosztálya.

2. Igazolja, hogy ha $\displaystyle H_1$, $\displaystyle H_2$ a $\displaystyle G$ csoport részcsoportjai, akkor $\displaystyle |H_1*H_2|=\frac{|H_1|*|H_2|}{|H_1\cap H_2|}$

3. Igazolja, hogy bármely $\displaystyle G$ csoportra, és annak bármely $\displaystyle H_1$, $\displaystyle H_2$ részcsoportjára $\displaystyle H_1\cup H_2$ pontosan akkor részcsoport, ha $\displaystyle H_1\subseteq H_2$, vagy $\displaystyle H_2\subseteq H_1$.

Előre is köszönöm mindenki segítségét.

Maximum weight matching a wikipedian, es ott is van a Blossom algorithm alul, Edmonds-tol. Ilyen kerdeseknel erdemes megkeresni, hogy mi az angol megfeleloje a problemakornek az absztrakcios lepes utan (ie. minimalis osszsulyu pariositast keresunk egy sulyozott grafban), onnettol meg altalaban meg is van a tetel neve par perc alatt.

Egy országban 128 város csapata nevezett egy kupasorozatra. Ismertek a városok közti utazási távolságok. Hogyan kell párokat készíteni a 128 csapatból, hogy az össz utazási távolság minimális legyen? (gyors algoritmus) Mindenki segítségét előre is köszönöm.

Ismert, hogy hogyan lehet meghatározni egy háromszögbe írt Malfatti-körök sugarait. De hogyan lehet meghatározni egy háromszög egy oldalához írt Malfatti-körök sugarait? Mindenki segítségét köszönöm előre.

15 eve ugyan, de ez is szerepelt mar a pontversenyben: B. 4154. :)

Délben a kör alakú városfal 12 őre napi ellenőrző útjára indul. Mindenki saját őrhelyéről indul az óramutató járásával megegyező vagy ellentétes irányba, és akkora állandó sebességgel halad, hogy 1 óra alatt tenne meg egy kört. Azonban, ha két őr találkozik, akkor mindketten rögtön megfordulnak, és változatlan sebességgel haladnak tovább. Igazoljuk, hogy éjfélkor minden őr ugyanott lesz, ahonnan délben indult!

A kérdésre adott válasz megfogalmazásához szerintem először tisztáznod kellene, hogy mit értesz "alakzat területe" alatt, de úgy, hogy "az eljárásban NE legyen végtelen sor és NE legyen határérték, és NE legyen differenciálszámítás vagy integrálszámítás, mert hogy ezek nem elemi módszerek". :)

Ha a d) rész annak az esélye, hogy Törpapa és Törpilla ugyanabban az ajándékozási ciklusban szerepelnek, akkor az könnyű.

A c)-re a válasz k-tól függetlenül 1/100 (és n darab törp esetén 1/n), amiből a b), majd az a) is adódik. Bizonyítás pl https://math.ucr.edu/home/baez/permutations/permutations_6.html, a lap alján, alulról a második.

Az e) kijön például rekurzívan felírva, az eredmény https://oeis.org/A001818 : "Number of permutations in $\displaystyle S_{2n}$ in which all cycles have even length".

Aprajafalván a hupikék törpikék megjándékozzák egymást. (Tegyük fel, hogy 100 törp van, köztük Törpapa és Törpilla.) Hogy ki kinek fog ajándékot adni, azt sorsolás útján döntik el: mindenki felírja a nevét egy kis papírra, a papírt beleteszik Törpapa sapkájába, majd mindenki egy cetlit húz a sapkából. Minden törp azt a törpöt ajándékozza meg, akinek a nevét húzta. Így könnyen előfordulhat, hogy valaki a saját nevét húzta, ebben az esetben az illető törp saját magának készít ajándékot.

a.) Az összes ajándékozási lehetőséget tekintve hány ajándékozási ciklus van az 1 hosszú ciklusokat is beleértve?

b.) Az összes ajándékozási lehetőséget tekintve hány "k" hosszú ajándékozási ciklus van?

c.) Mennyi annak a valószínűsége, hogy Törpapa egy "k" hosszú ajándékozási ciklusban szerepel?

d.) Mennyi annak a valószínűsége, hogy Törpapa és Törpilla az ajándékozási ciklusban szerepel?

e.) Hány olyan ajándékozási lehetőség van a 100 törp között, amelyben minden ciklus hossza páros?

Minden segítséget előre is köszönök. BZ.

Erre azért tényleg kíváncsi vagyok most már magam is.

(a határérték felhasználása nélküli megoldásokról az a közismert "bizonyítás" jut eszembe, amely szerint a négyzet átlója az oldalak összegével egyenlő)