| [24] Geg | 2004-06-01 21:59:24 |
 Velemenyem szerint az adatok nyilvan rosszak, a feladat kituzoje ugy gondolta, hogy a folyamatra ervenyesek a Poisson egyenletek, csak elirta.
Egy folyamat nem tekintheto kvazisztatikusnak, ha a gaz belsejeben szamottevo orvenyles lep fel, ekkor ugyanis nem ervenyes ra az allapotegyenlet, mert az csak egyensuly esetere igaz. El lehet gondolkozni, hogy jo kozelites-e a gyors folyamatoknal megis ezt felhasznalni, de kozepiskolas szinten ez szerintem meg rendben van. Foleg azzal a tudattal, hogy mar az idealis gaz modell is csak egy kozelites.
|
| Előzmény: [23] Kós Géza, 2004-06-01 20:28:58 |
|
| [23] Kós Géza | 2004-06-01 20:28:58 |
 Olvasgatva a vitát, egy-két dolog még eszembe jutott. (Ha netán hülyeségeket írnék, az azért van, mert a fizikához csak a középiskolás szinten értek.)
Az egész kvázisztatikus / nem kvázisztatikus dolog onnan jött elő, hogy a feladatban a megadott adatokkal 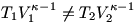 , és az elmélet úgy szólt, hogy esetleg a megadott adatok rendben vannak, csak éppen a folyamat nem kvázisztatikus. , és az elmélet úgy szólt, hogy esetleg a megadott adatok rendben vannak, csak éppen a folyamat nem kvázisztatikus.
Azért, hogy kicsit visszatérjünk a földre, idézzük fel, hogy mi is volt a feladat. Egy 20 millis orvosi fecskendőt (kézzel) benyomunk 16-ig olyan "gyorsan", hogy a hőkiegyenlítődés elhanyagolható legyen, és a folyamatot adiabatikusnak lehessen tekinteni. Ez azt jelenti, hogy a dugattyú a 2-3 centiméteres utat néhány tized, esetleg néhány század másodperc alatt teszi meg. A dugattyú sebessége legfeljebb néhányszor tíz cm/s.
Ha a folyamat nem tekinthető kvázisztatikusnak, az azt jelenti, hogy a dugattyú sebessége legalábbis összemérhető a hangsebességgel, de mindenképpen több tíz m/s. Vagy nem? Mekkora sebesség kellene ahhoz, hogy a folyamatot ne lehessen kvázisztatikusnak tekinteni?
* * *
Ha a 20 köbcentiméternyi, 16 fokos levegőt 16 köbcentire nyomjuk össze adiabatikusan és kvázisztatikusan stb., akkor a végzett munka a 2. megoldás szerint számítható: 0,46J. Ennél kisebb eredményt semmilyen esetben sem kaphatunk. Mégis, az 1. megoldás szerint a munka csupán 0,1J. (Máris kész az örökmozgó. Összenyomjuk a gázt 0,1J munkával, utána hagyjuk kvázisztatikusan kitágulni, miközben négy és félszer annyi energiát termel... :-) )
Ez is mutatja, hogy a megadott adatok biztosan hibásak. (A véleményem egy kicsit változott. Most arra szavaznék, hogy a T2 a hibás; a feladat kitűzője a T2 kiszámításakor hibázott, és 16 helyett tévedésből 19 köbcentiméterrel számolt.)
* * *
Arra mindenképpen jó ez a téma, hogy sokat lehet belőle tanulni.. :-)
|
|
|
| [21] Geg | 2004-05-30 16:46:23 |
 Tekintsunk vakuumban egy tartalyt, melyben adott mennyisegu gaz van es melyet dugattyu zar el a kulvilagtol. Ha a dugattyut hirtelen elengedjuk, az nyilvan elindul "kifele". A kulso nyomas ekozben vegig nulla ! Felirva az elso fotetelt a munka megsem nulla, hiszen a gaz erot fejt ki a dugattyura, Newton torvenye miatt az is erot fejt ki a gazra. A munka a GAZ nyomasanak terfogat szerinti integralja (helyes elojellel), nem pedig a kulso nyomase. A folyamatra szigoruan nezve azert nem igazak a Poisson egyenletek, mert a nyomast csak kvazisztatikus folyamat soran szamithatjuk ki az allapotegyenletbol.
|
| Előzmény: [20] gxa, 2004-05-30 00:14:50 |
|
| [20] gxa | 2004-05-30 00:14:50 |
 Pont ez a probléma, hogy nem írható át! Ugyanis az első főtételben a gázon végzett munka szerepel, ami pkülső  V alakú. A gáz nyomása csak akkor lesz egyenlő ezzel a pkülső értékkel, ha a folyamat kvázisztatikus. V alakú. A gáz nyomása csak akkor lesz egyenlő ezzel a pkülső értékkel, ha a folyamat kvázisztatikus.
|
|
| [19] Geg | 2004-05-27 12:31:55 |
 Hat sztem a munkavegzes mindig atirhato a -pdV alakra, viszont a nyomas csak kvazisztatikus folyamatok eseten adhato meg a p = nRT/V kifejezessel (amit fel kell hasznalni a Poisson egyenletek levezetesekor).
|
| Előzmény: [18] gxa, 2004-05-26 15:37:38 |
|
| [18] gxa | 2004-05-26 15:37:38 |
 Kedves Géza!
Úgy látszik, hogy rosszul fejeztem ki magam. Szerintem is ideális gázról van szó a feladatban, más eset nem igazán lenne fair...
Az első főtétel differenciális formában írható így:
 U= U= Q+ Q+ W W
Itt arról van szó, hogy az utolsó tagot csak akkor írhatjuk át  W=-p W=-p V alakba, ha a folyamat során végig egyensúlyi állapotokon megyünk át. Ez esetben csakugyan levezethetőek a Poisson-képletek. Azonban ha ez nem igaz, akkor csak az általánosabb képlet marad érvényben, és ekkor csak azt tehetjük meg, hogy a kezdő- és végállapot között írjuk fel az összefüggést, kihasználva, hogy V alakba, ha a folyamat során végig egyensúlyi állapotokon megyünk át. Ez esetben csakugyan levezethetőek a Poisson-képletek. Azonban ha ez nem igaz, akkor csak az általánosabb képlet marad érvényben, és ekkor csak azt tehetjük meg, hogy a kezdő- és végállapot között írjuk fel az összefüggést, kihasználva, hogy  Q=0 végig igaz, és így kapjuk (továbbra is feltéve, hogy ideális gázról van szó), hogy: Q=0 végig igaz, és így kapjuk (továbbra is feltéve, hogy ideális gázról van szó), hogy:

Lényegében arra akartam kilyukadni, hogy a "gyorsan nyomjuk be a dugattyút" jó eséllyel erre az esetre utal.
Ajánlott irodalom: Budó: Kísérleti fizika 1. 119.§, 388. oldal.
Üdv.
|
|
| [17] Kós Géza | 2004-05-26 13:22:05 |
 Kedves Attila,
Köszi a sok információt. Most már pontosabban értem, hogy mire gondoltál.
A kérdés az, hogy a feladat kitűzője a fecskendőben levő levegőt ideális gáznak tekintette-e. A Te elméleted az, hogy (esetleg) nem tekintette ideálisnak, és emiatt nem alkalmazhatók az ideális gázokra érvényes képletek.
A kulcs szerintem az a mondat, hogy ,,a levegő gyakorlatilag kétatomos molekulákból áll''. Ezzel szerintem sugallja, hogy a levegőt ideális gáznak tekinti és f=5.
Még egy apróság. Ezer bocs a kötekedésért (tényleg), de nem értek teljesen egyet azzal, hogy az 1. megoldás általánosabb, nem ideális gázokra is érvényes törvényeket használ fel. Az 1. megoldás felhasználja a gáztörvényt az N kiszámításához, a belső energia megváltozását a 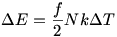 képletből számítja ki. Ha ezek a képletek a teljes folyamat során igazak maradnak, akkor levezethető belőlük, hogy képletből számítja ki. Ha ezek a képletek a teljes folyamat során igazak maradnak, akkor levezethető belőlük, hogy  és és 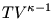 állandó. állandó.
* * *
Most már ideje kiszállnom a vitából, inkább csak olvasni szeretném. Remélem, nem voltam elviselhetetlenül okoskodó. :-)
Üdv.
Géza
|
| Előzmény: [14] gxa, 2004-05-26 02:03:14 |
|
| [16] Geg | 2004-05-26 12:17:13 |
 Egy allapotvaltozast adiabatikusnak hivunk, ha a hokozles nulla. Ebbol a feltetelbol az elso fotetel felhasznalasaval egyenesen kovetkeznek a Poisson-egyenletek, igy nem ertem miert tartod helytelen beidegzodesnek. Termeszetesen idealis gaz eseterol beszeltem, de hat kozepiskolaban csak az fordul elo.
|
| Előzmény: [14] gxa, 2004-05-26 02:03:14 |
|
| [15] syllabus | 2004-05-26 09:51:44 |
 A megoldási útmutatóban nem jelzik, hogy azért választják az 1. megoldást, mert nem kvázisztatikus folyamatról van szó, és a többi út hibás választás lenne.
Valószínűleg, ők is csak véletlenül választották a jó megoldást. :)
Ettől persze a gyerekek észrevehették volna... :)
|
| Előzmény: [14] gxa, 2004-05-26 02:03:14 |
|
| [14] gxa | 2004-05-26 02:03:14 |
 Kedves Géza!
A 16-19 tényleg érdekes egybeesés, tehát ez is egy lehetséges feloldás. Azt viszont fenntartom, hogy az adiabatikus állapotváltozás -> TV**(k-1)=állandó beidegződés helytelen középiskolai szinten is. Ennek oka talán az, hogy az adiabatikus folyamatokra mindig a gyors változásokat hozzák fel példaként, nem (eléggé) kihangsúlyozva, hogy erre azért van szükség, hogy ne legyen idő hőcserére, és a Poisson-képletek csak bizonyos feltételek mellett igazak ("gyors" változásoknál pont nem). Jómagam is belefutottam egyszer ebbe még kilencedikesként, azóta figyelek erre ennyire :) Visszatérve a feladatra, szerintem csak a kitűző tudhatja, hogy melyik hipotézis a helyes :), őt kellene megkeresni...
Üdv.
|
|
| [13] syllabus | 2004-05-25 20:55:27 |
 Hát ez nagyszerű! Akkor ez jó példa volt, ha minden megoldás elfogadható! ;)
A kvázisztatikus folyamatról írna valaki néhány sort? Valahol tanítják középiskolában?
Köszönöm a válaszokat!
Syllabus
|
|
| [12] Kós Géza | 2004-05-25 15:54:17 |
 Kedves Attila,
Szerintem a feladat nem a megoldás módszerétől vagy a felhasznált fizikai törvényektől válik túlhatározottá, hanem már eleve túlhatározott, pontosabban ellentmondásos.
-- Megmondták, hogy kétatomos gázról és adiabatikus folyamatról van szó, tehát a folyamat során 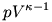 állandó. állandó.
-- Megadták a hőmérsékletet és a térfogatot mindkét állapotban.
-- A megadott információk ellentmondanak egymásnak.
Én úgy gondolom, hogy azért adtak meg ennyi adatot, hogy a feladatot sokféleképpen -- az adiabatikus folyamat ismerete nélkül is -- meg lehessen oldani, és az egyik számot elgépelték.
Ha találgatni akarunk, hogy melyik adat lehet a hibás, akkor mind a négy adatra kiszámíthatjuk, hogy milyen más érték esetén teljesülne a törvény.
-- a T1 értéke 16 fok helyett -3 fok;
-- a T2 értéke 21,8 fok helyett 43 fok;
-- a V1 értéke 20 helyett 16,8 köbcentiméter;
-- a V2 értéke 16 helyett 19 köbcentiméter;
-- a folyamat nem is adiabatikus.
Az utolsó lehetőséget elvethetjük, mert a nyomás sem állandó, és ha hőközlés is van, a munka kiszámítására nincs esélyünk.
A többi lehetőség közül csak a 16 helyett 19 tűnik reálisnak; a 9-es számjegy helyett véletlenül 6-ost írtak, ráadásul a 19 köbcentiméter feltűnően pontos érték.
* * *
Az 1. megoldás nem azért szerencsésebb a többinél, mert ,,általánosabb'' törvényt használ, hanem azért, mert nem használja V2-t, míg a többi megoldás az összes adatot felhasználja.
A teljesen korrekt megoldás szerintem az, ha először rámutatunk, hogy az adatok ellentmondanak, utána megmondjuk, hogy a négy adat közül melyik háromból számoljuk ki az eredményt, végül ki is számoljuk.
Egy felvételin, különösen egy 3. feladatban ezt nem lehet elvárni, szerintem mindegyik megoldásra a maximális pontszámot kell adni. Versenyen más a helyzet, ott többre kell értékelni azt, aki észreveszi és kezeli az ellentmondást.
|
| Előzmény: [11] gxa, 2004-05-25 14:24:28 |
|
| [11] gxa | 2004-05-25 14:24:28 |
 Sziasztok!
Itt arról van szó, hogy ha felhasználjuk a Poisson-képleteket, akkor a feladat túlhatározottá válik, ami azért jó, ha feltűnik, függetlenül attól, hogy az illető milyen szinten tanulta a hőtant. Ezzel szemben a hőtan első főtételén alapuló megoldás nem feltételez semmit a folyamatról, hiszen az sokkal általánosabb esetben működik. Másrészt az adiabatikus folyamat definíciója az, hogy hőátadás nincs, és nem az, hogy Poisson-képletek érvényesek rá. Szerintem a feleslegesnek tűnő adat mindenképpen rá kellene, hogy vezessen, hogy itt valami nincs rendben... Ha pedig nincs, akkor vissza kell nyúlni egy olyan képlethez, ami egész biztosan működik, és ez az első főtétel.
Üdv.
|
|
|
| [9] lorantfy | 2004-05-24 23:02:24 |
 Kedves Syllabus!
Szerintem az általad leírt mindhárom megoldást teljes értékű megoldásnak kell elfogadni, attól függetlenül, hogy számszerűen más eredményre vezetnek. A középiskolában, ha egyáltalán marad idő az adiabatikus folyamat tárgyalására, akkor azt tanítjuk, hogy a gyakorlatban olyan esetekben valósul meg - jó közelítéssel - ahol jól szigetelt a rendszer, vagy olyan gyors a folyamat, hogy nincs idő a hőátadásra.
Mivel a feladat szövegében benne van, hogy a folyamat adiabatikus, a diák teljes joggal használhatja a megtanult, vagy a fgv. táblában adiabatikus állapotváltozás címszó alatt talált képleteket.
1. megoldás gondolatmenete: A folyamat adiabatikus, tehát nincs hőcsere a környezettel. Az összes végzett munka a belső energiát növeli. Tehát kiszámolom a belső energia változását. Még külön odaírták, hogy kétatomos gázokról van szó. f=5. Behelyettesítek a képletbe. Kész.
2. megoldás gondolatmenete: A folyamat adiabatikus, tehát használhatom a Poisson összefüggést. Megadták, hogy kétatomos gázokról van szó. 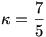 , igy ki tudom számolni a hiányzó p2 nyomást, majd behelyettesítek az adiabatikus folyamat tágulási munka képletébe. Kész. , igy ki tudom számolni a hiányzó p2 nyomást, majd behelyettesítek az adiabatikus folyamat tágulási munka képletébe. Kész.
3. megoldás gondolatmenete: Megadták az összenyomás utáni térfogatot, hőmérsékletet és tudom a részecskeszámot. Ált. gáztörvénnyel kiszámítom a hiányzó nyomást. Ismerem az adiabatikus folyamatra a tágulási munka képletét. Hoppá, ebben van egy furcsa betű. Fgv. tábla 133. oldalon benne van, hogy 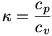 és még az is, hogy ez kétatomos gázra és még az is, hogy ez kétatomos gázra 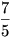 . Akkor beírom az adatokat a képletbe, kiszámolom és kész. . Akkor beírom az adatokat a képletbe, kiszámolom és kész.
Én bármelyik gondolatmenetért megadnám a c) részre járó 5 pontot.
|
| Előzmény: [8] syllabus, 2004-05-24 20:08:38 |
|
| [8] syllabus | 2004-05-24 20:08:38 |
 Kedves gxa!
A feladat szövegében a gyors összenyomás nyilvánvalóan csak arra vonatkozik, hogy a folyamat adiabatikus legyen, mert a feladat szövege fecskendőről szól és nem szigetelt hőtartályról.
Tudtommal a kvázisztatikus folyamat fogalma nem középiskolai anyag. Googleban rákerestem, de csak egyetemi jegyzetekben fordul elő.
Baranyi Károly kitűnő könyvében például ez olvasható: "adiabatikus folyamat valósul meg, ha valamely gázt egy tartályban gyors mozdulattal tágítunk, vagy hirtelen összenyomunk."
Egy diák nem tudhatja, hogy az adiabatikus folyamtokról tanult képletek egy része nem működik nem kvázisztatikus esetben, ráadásul a példa szövegéből sem következik, hogy nem kvázisztatikus folyamatról van szó.
Ezen a példán elúszhat egy felvételi!!!
|
|
| [7] lorantfy | 2004-05-24 19:24:57 |
 A feladat eredeti szövege:
3A Egy orvosi fecskendőben, amelynek kiömlőnyílását elzártuk, 16oC hőmérsékletű levegő van. A 2cm2 keresztmetszetű dugattyú a 20cm3-es jelnél áll. A külső és a bezárt levegő nyomása egyaránt 105Pa.
a) Hány molekula van a bezárt levegőben?
b) A dugattyút lassan, állandó hőmérsékleten benyomva a 16cm3-es jelnél tartjuk egyensúlyban. Mekkora erőt kell kifejtenünk ekkor?
c) Ha gyorsan nyomjuk be a dugattyút a 16cm3-es jelig, akkor a bezárt gáz adiabatikusan 21,8oC hőmérsékletre melegszik. Mennyi munkát végzünk a gázon a hirtelen összenyomás közben? (A levegő gyakorlatilag csupa kétatomos molekulából áll.) k = 1,38*10-23 J/K
A Géza által számolt arány nekem  0,93-ra jött ki, de a 21,8oC-os hőmérséklethez valóban 19cm3-es térfogat kellett volna megadni. 0,93-ra jött ki, de a 21,8oC-os hőmérséklethez valóban 19cm3-es térfogat kellett volna megadni.
Vagy a 16cm3-es térfogathoz (mivel ez a szám a b) kérdésben is szerepelt) 316K=43oC-os hőmérsékletet.
|
| Előzmény: [3] Ka_Csa, 2004-05-24 15:55:06 |
|
| [6] gxa | 2004-05-24 19:01:59 |
 Sziasztok!
Én egy negyedik helyett a hivatalos megoldásra szavazok. A többi ugyanis csak akkor használható, ha kvázisztatikus folyamatról van szó, a feladat szövege szerintem ezt kizárja. Ez érvényes a Kós Géza által írt képletre is.
Üdv.
|
|
| [5] syllabus | 2004-05-24 17:41:51 |
 Bocs Géza! Nem tudom miért Csabát írtam. Teljesen megzavarodtam.... :)
|
|
| [4] syllabus | 2004-05-24 17:40:36 |
 Köszi Csaba!
Emberek! Akkor most mi van?! Rossz volt a felvételi feladatsor egyik példája?
Hol lehet ennek utánanézni?
Minden megoldást elfogadnak, vagy törlik a feladatot?
Segítséééééég!
|
|
|
| [2] Kós Géza | 2004-05-24 09:49:06 |
 Nem tudom, hogy mi volt a pontos feladat, de úgy tűnik, hogy legalábbis az itt megadott adatok ellentmondanak egymásnak.
Adiabatikus folyamat esetén ugyanis 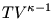 állandó, a megadott adatokkal azonban állandó, a megadott adatokkal azonban
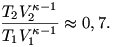
Ettől kezdve, attól függően, hogy milyen adatokat használunk fel, más és más lesz az eredmény.
Egy kis keresgéléssel kitalálható, hogy valószínűleg a második térfogatot írhatta el valaki: nem 16, hanem 19 köbcentiméter.
|
| Előzmény: [1] syllabus, 2004-05-24 00:37:36 |
|
| [1] syllabus | 2004-05-24 00:37:36 |
 A fizika felvételi 3A feladata így szólt:
3A Egy orvosi fecskendőben, amelynek kiömlőnyílását elzártuk, 16 oC hőmérsékletű levegő van. A 2cm2 keresztmetszetű dugattyú a 20cm3-es jelnél áll. A külső és a bezárt levegő nyomása egyaránt 100000 Pa. c) Ha gyorsan nyomjuk be a dugattyút a 16cm3-es jelig, akkor a bezárt gáz adiabatikusan 21,8 oC hőmérsékletre melegszik. Mennyi munkát végzünk a gázon a hirtelen összenyomás közben? (A levegő gyakorlatilag csupa kétatomos molekulából áll.)
k = 1,38*10-23 J/K
Tehát, ha jól értem:
P1=100000 Pa V1=0,00002 m3 T1=289 K
P2=? V1=0,000016 m3 T1=294,8 K
1. megoldás: (hivatalos ;) Q=0 W=dE dE=f/2*N*k*dT dT=T2-T1 W=f/2*N*k*dT W=0,1 J
2. megoldás: (?) Poisson-egyenlet: P1*(V1 ad k)=P2*(V2 ad k) P2=136669 Pa Tágulási munka: W=(P1*V1-P2*V2)/(k-1) W=0,46 J
3. megoldás: (?) Általános gáztörvényből: P2=127000 Pa Tágulási munka: W=(P1*V1-P2*V2)/(k-1) W=0,8 J
Melyik megoldás miért jó és miért nem?
Köszönet!
syllabus
ps: Várom a negyedik variációt... ;)
|
|
