| [466] sakkmath | 2022-11-21 23:54:26 |
 Köszönöm az összefoglalót és a három linket. Az elsőből kiindulva eljuthatunk a Wolfram Alpha ezen oldalára, ahol a 8 x 8-as táblára megkapjuk a mágikus összeget, a 260-at, ami konstans. A szóban forgó (huszár)túrák tündérsakkfeladványoknak is tekinthetők. Exner Kornél dr. magyar sakkfeladványszerző 54 találattal – huszárbejárással – szerepel a 3. hivatkozásodon. Rövid ismertetőt itt olvashatunk róla (a karakter/helyesírási hibákat nézzük el).
|
| Előzmény: [464] jonas, 2022-11-16 14:20:42 |
|
|
| [463] sakkmath | 2022-11-11 23:24:40 |
 A 8 x 8-as sakktábla egyik mezőjéről elindul egy huszár és bejárja a teljes táblát. Az útvonal mezőit az időrend szerint megszámozzuk: a kiindulási mezőre az 1-es számot, a következőre a 2-es számot írjuk, és így tovább.
Keressünk egy bejárást, melyre teljesül, hogy a tábla minden sorában és oszlopában a beírt számok összege egy rögzített n szám.
Hány huszárbejárás létezhet? Lehet-e közöttük olyan, amelyben a két nagyátlóba írt számok összege is megegyezik a sorokba és az oszlopokba írt számok összegével?
|
 |
|
| [462] Róbert Gida | 2021-05-08 22:50:36 |
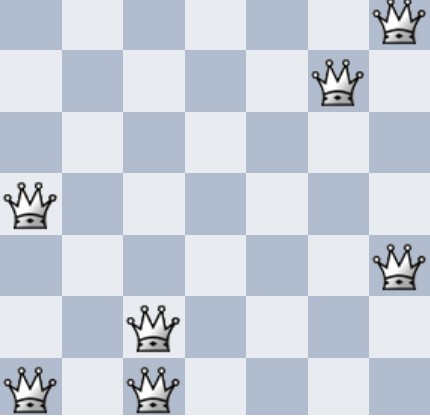
 7x7-esre egy megoldás a hozzászólás alján amit programmal találtam! Úgy látom, hogy 8 megoldás van, azaz lényegében egy különböző, a többi ennek az elforgatottja, tükörképe [, mivel |D4|=8 és az eredeti ábrának nincs szimmetriája].
Míg a 8x8-asra nincs megoldás! Géppel ez gyorsan kijön, mármint, hogy nincs megoldás, néhány másodperc. Anélkül nem látom: van 33 féle lehetséges távolságnégyzet, ami 0<d=x2+y2 alakú, ahol x,y<8. De nekünk \displaystyle \binom {8}{2}=28 különböző távolságösszegnek kell lennie. Így ez alapján még lehetne... De azt egyébként olcsón mutatja, hogy kilencet már nem lehet felrakni, mert \displaystyle \binom{9}{2}=36>33 .
|
 |
| Előzmény: [461] sakkmath, 2021-05-05 15:30:16 |
|
| [461] sakkmath | 2021-05-05 15:30:16 |
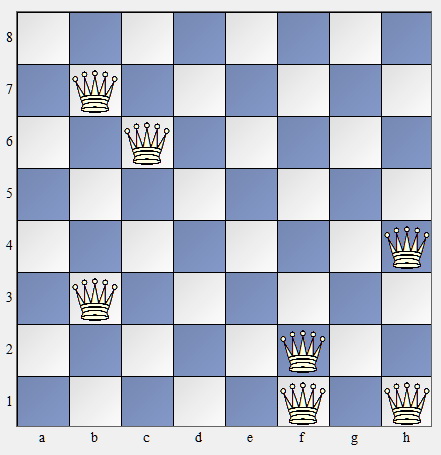
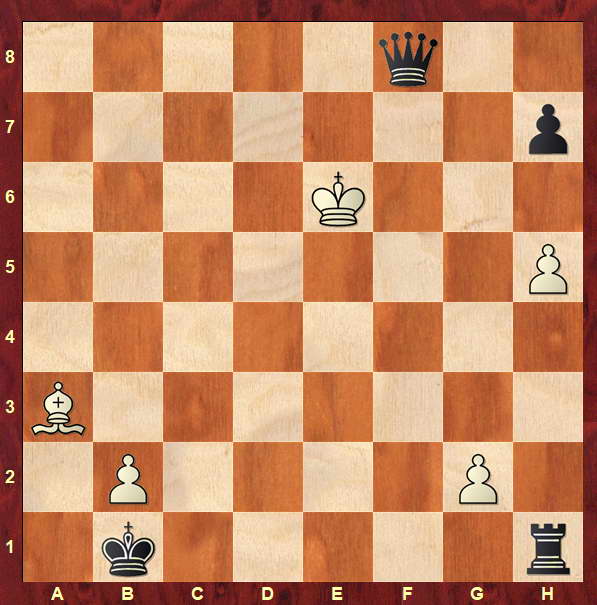
 Közeledik a 3 éves évforduló (...). Az egyetlen (!) megoldás:
\displaystyle 1. Va2-{\bf f2}, 2. Va4-{\bf h4}, 3. Va6-{\bf f1}, 4. Va8-{\bf h1}, 5. Vc8-{\bf b7}, 6. Ve8-{\bf c6}, 7. Vg8-{\bf b3}. (Ábra lent.)
Pótfeladat: Mi lehet a megoldás, ha a \displaystyle 7 vezért tetszés szerinti sorrendben, a „levegőből” rakjuk fel a \displaystyle 7 x 7-es táblára?
Pót-pót feladat: Létezik-e megoldás, ha a „levegőből” \displaystyle {\bf 8} vezért kell felrakni a \displaystyle {\bf 8x8}-as táblára (úgy, hogy a páronkénti távolságok mind különbözőek legyenek)?
|
 |
| Előzmény: [455] sakkmath, 2018-05-19 19:54:06 |
|
|
| [459] SmallPotato | 2020-04-08 16:58:43 |
 Biztos az, hogy a sötét vezér a leírt módon (azaz mezőközéppontokat összekötve) szabályos nyolcágú csillagot jár be? Nekem úgy tűnik, hogy az így kapott csillag burkolónyolcszögének oldalai felváltva \displaystyle 3 egység, ill. \displaystyle 2\sqrt2 egység hosszúságúak, ha a sakktábla egy mezője egységoldalú négyzet.
(A C. 1449. feladatban [2017. december] valóban szabályos, tehát nem vezér-bejárta csillag szerepelt.)
|
| Előzmény: [458] sakkmath, 2020-04-01 23:12:14 |
|
| [458] sakkmath | 2020-04-01 23:12:14 |
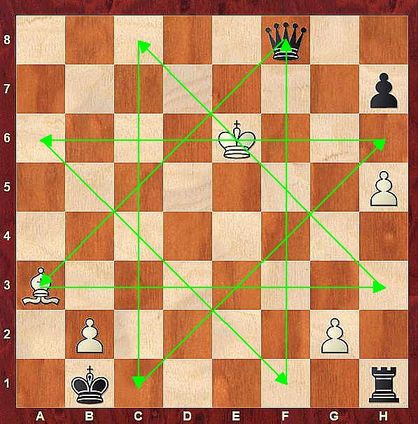
 Az alábbi, kissé pontatlan ábrán a sötét vezér útját a csatlakozó vektorok mutatják.
Szerkesztő programmal elérhető, hogy a vektorok az indulási/érkezési mezők középpontjait kössék össze. Ekkor a vezér útja szabályos nyolcágú csillag lesz, melynek oldalai felváltva illeszkednek a sakktábla megfelelő mezőinek (négyzeteinek) átlóira, illetve középvonalaira.
A C. 1449. feladat e csillag kerületét kérdezte.
|
 |
| Előzmény: [457] sakkmath, 2020-04-01 23:04:53 |
|
|
| [455] sakkmath | 2018-05-19 19:54:06 |
 Remélem, hogy az előző, [454]-es feladványra hamarosan befut a megoldás. Addig is következzék egy újabb távolságprobléma.
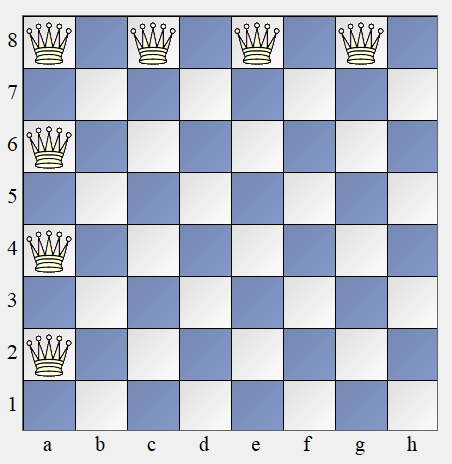
A szerző Bán Jenő.
Helyezzünk el hét vezért a sakktáblán az ábrán látható módon. Az a2, a4, a6, a8, c8, e8 és g8 vezérekkel egymás után tegyünk egy-egy szabályos lépést úgy, hogy mind a hét vezér a tábla üresen lévő, 7x7-es területére kerüljön és minden távolság, ami 2-2 vezér között lemérhető, különböző legyen.
|
 |
|
| [454] sakkmath | 2018-05-06 16:01:17 |
 Az alábbi ábrán Dawson és Pauly szerzeményét láthatjuk 1920-ból, a The Chess Amateur-ből. Követelménye:
Távlépő önmatt 8 lépésben.
Bővebben:
Világos indul és kényszeríti sötétet, hogy a nyolcadik lépésben mattot adjon neki. A „távlépő” jelentése itt: sötét köteles mindig a leghosszabb lépést húzni.
(Ezt a feladványt a KöMaL 2017. decemberi számának C. 1449. feladata juttatta eszembe…. .)
|
 |
|
| [453] sakkmath | 2017-11-05 23:06:12 |
 Két hónap után sincs jelentkező, ezért megadom a furcsa játszma helyét.
https://www.youtube.com/watch?v=7B9p2PrsKWY
Érdemes a hozzászólásokat is átfutni (csak győzzük!). Az eltérő vélemények mérlegelése után nem könnyű állást foglalni a 2000. évi online Fischer(?) - Short villámmeccsről.
|
| Előzmény: [452] sakkmath, 2017-09-03 23:46:53 |
|
| [452] sakkmath | 2017-09-03 23:46:53 |
 Láttuk, hogy 1.f4 után világos – saját, gyors vesztése érdekében – 2.Kf2-t, majd 3.Kf3-at lépte.
Állítólag két világhírű sakkozó játszott egy partit, ahol világos 51 lépésben nyert és az első háromban rendre ezeket húzta! (Sötét lépései eltértek.)
Keressük meg ezt a játszmát és mondjunk véleményt róla!
|
| Előzmény: [447] sakkmath, 2017-07-15 22:46:39 |
|
|
| [450] sakkmath | 2017-07-18 17:17:31 |
 A felsorolásodat máris frissítem ezzel: ... Gyalog: 4 ... :-)
Jó félórája én is feliratkoztam az oldalra, s feltettem ide, 38. hozzászólóként a 4 lépéses gyalogmattomat, ezt:
1.e4 e5 2.Fd3 d5 3.Ke2 Fg4+ 4.Ke3, d4#.
Ebben a kategóriában tehát ez az új és végleges rekord.
|
| Előzmény: [449] Sirpi, 2017-07-18 08:28:55 |
|
| [449] Sirpi | 2017-07-18 08:28:55 |
 Közben itt találtam egy topikot, ahol a leggyorsabb mattokat szedik össze. Beírtam a 6 lépéses sáncolósat, linkelve sakkmath eredeti hozzászólását, ami ott is új rekord volt, az ottani 7 lépéses helyett. Jelenleg így áll:
Vezér: 2 - Futár: 3 - Huszár: 3 - Bástya: 5 - Király: 6 - Gyalog: 5 - Sáncolás: 6 - Gyalog-átváltozás: 6 - En passant: 6
|
| Előzmény: [447] sakkmath, 2017-07-15 22:46:39 |
|
| [448] Sirpi | 2017-07-17 13:29:14 |
 Szép! Kár, hogy a világos utolsó lépése töltelék, de nem látom, hogyan lehetne a lépésszámot még 1-gyel lejjebb szorítani.
Amúgy ez volt az enyém, itt a két ló viszi el a sok időt:
1. Hh3 Hh6 2. Hg5 Hg4 3. Hxf7 Hxf2 4. Kxf2 e6 5. Ve1 Vg5 6. Hd6+ Fxd6 7. Bg1 O-O#
|
| Előzmény: [447] sakkmath, 2017-07-15 22:46:39 |
|
| [447] sakkmath | 2017-07-15 22:46:39 |
 Kiagyaltam ezt a 6 lépésest:
1.f4 e6 2.Kf2 Fc5+ 3.Kf3 Vh4 4.f5 Hh6(v. He7) 5.fxe6 fxe6 6.h3 0-0# (ábra a hsz. végén).
A mattállást a két fél eltérésekkel (lépéscserékkel) is kihozhatja. Világos 6.h3 helyett 9 másikat is húzhat.
Lesz-e valaki, aki kiötöl egy 5 lépésest? :-)
|
 |
| Előzmény: [446] Sirpi, 2017-07-13 14:06:46 |
|
| [446] Sirpi | 2017-07-13 14:06:46 |
 A múltkor a legrövidebb pattal végződő játszmát kerestem. A mai kérdés (amire nem tudom a választ) az, hogy hány lépésből áll a legrövidebb olyan parti, melyben a mattadó lépés sáncolás. 7 lépésest már találtam.
|
|
| [445] Matthew | 2017-06-29 02:38:44 |
 Üdv!
Sötét nem feltétlenül veszít minőséget a 22...Vxg7-es variban, de persze elég előnytelen lenne számára (23.Fxg5 Be8 24.Fh6 Vh7 például, majd a futó ellépése esetén vezércsere, de sötét ezek után elég rosszul állna).
A 22...Kxg7-es varit én is döntetlennek látom egyelőre. Ha hosszú sánccal kezdünk, sötét 22...gxh6-tal válaszol, ami nagyjából át is húzna mindent. A hxg7-es kezdés után én ezt találtam a legerősebbnek: 22...Kxg7 23.Fxg5 Kf7 24.Vh7+ Vxg7 (24...Vxh7 25.Bxh7+ Ke8 26. Bc7 és valamelyik sötét tiszt esik) 25.Bxg7+ Kg6 26.Bh5 Kf7 27.f4 de ez döntetlennek néz ki.
|
| Előzmény: [444] nadorp, 2017-06-27 03:02:45 |
|
| [444] nadorp | 2017-06-27 03:02:45 |
 Módosítok. 22.hxg jónan tűnik.
Ha erre sötét válasza 22.,Be8 vagy 22.,Bd8, akkor 23.Vh8,Kf7 24.Bh7 nyer.
Ha sötét válasza 22.,Vxg7, akkor 23.Fxg5 jön. A futó nem üthető 24.Vh7 matt miatt, a sötét vezér sem léphet,mert védtelenül hagyná a h8 mezőt és 24.Vh8 után veszítene. Így sötét bármit is lép 24.-ben, 25.Ff6 vagy vezé rt vagy minőséget nyer.
Ha sötét válasza 22.,Kxg7, akkor megint 23.Fxg5 jön. A futó most sem üthető 24.Vh7 matt miatt. Fenyeget 24.Fh6, ezért 23.,Kf7. Innen számomra nem egyértelmű világos hogyan nyer. Talán ahogy az elózóben írtam, vezért cserél h5-ön, hosszút sáncol és beviszi a szabad gyalogokat
|
| Előzmény: [442] sakkmath, 2017-06-24 15:13:31 |
|
| [443] nadorp | 2017-06-26 23:55:59 |
 Nem vagyok, nagy elemző, de úgy látom, hogy sötét királyszárnya a vezér nélkül elég gyenge, ezért logikus lenne egy vezércsere. Utána a sötét g gyalog nem védhető, majd világos elindul az f és g gyaloggal. A tervhez először 22.0-0-0 kéne,ez egyrészt védi a c2 gyalogot,másrészt az a1 bástya eljutna az f-vonalra és védené az f2 gyalogot, így a futó felszabadulna. Tervem: 22.0-0-0 23.Bdf1 24.f3 25.Vh5
A nagyon csábító 22.h7,Kh8 (a 22.,Kf7? 23.h8H miatt nem jó sötétnek minőség vesztés miatt) vagy 22.hxg lépésekre nem találtam meg a jó folytatást
|
| Előzmény: [442] sakkmath, 2017-06-24 15:13:31 |
|
| [442] sakkmath | 2017-06-24 15:13:31 |
 Üdv!
Célszerű megtartani a játszma lépésszámozását.
Ennek megfelelően:
20.Hxg5,Ve7? 21.Hf3 után sötét - ellenérték nélkül - gyaloghátrányban marad. Ezzel tehát nem érdemes foglalkozni.
Nézzük ezt a változatot:
20.Hxg5, hxg5 21.h6, Vg6 (Ábra.)
Itt mi a legjobb folytatás? Mi lesz a végeredmény?
|
 |
| Előzmény: [439] Matthew, 2017-06-05 13:38:22 |
|
| [441] sakkmath | 2017-06-24 13:31:53 |
 A feladvány szerzője Benkő Pál. A figurák az 5 számjegyet formázzák.
A sakk szabályai szerint az utolsó (fél)lépést nem tehette sötét. Utoljára tehát csak világos léphetett, így most sötéten a sor.
A megoldás ennek megfelelően: 1.a6xb5 (lépéskényszer volt), Bxa7 matt!
|
| Előzmény: [435] sakkmath, 2016-02-14 00:01:52 |
|
|
