| [60] Pach Péter Pál | 2004-06-09 21:54:12 |
 Ezt a kérdést igazából az egyik matektanárom, Surányi László tette fel nekem. A feladatot "megöli", ha nem 0 reakcióidővel számolunk. A fizikai problémák, amiket említesz, nem lényegesek, mert ez egy matekfeladat. (Szóval nem az idealizált feltételekkel van a gond.) A 0 reakcióidővel logikai problémák vannak. Surányi tanár úrt fogalmilag nagyon zavarta a dolog. A megoldás jó, ha tudjuk, hogy stratégiájukat mindketten meg tudják valósítani.
|
| Előzmény: [59] Kós Géza, 2004-06-09 20:27:12 |
|
| [59] Kós Géza | 2004-06-09 20:27:12 |
 Hát ebbe most nem szeretnék nagyon belemenni. A feladat a p0 szám megtalálása volt idealizált feltételek (pontszerű szereplők, 0 reakcióidő) mellett.
A reakcióidő mellett ugyanígy számíthatna, hogy hogyan veszi be Tom a kanyart a medence szélén, és milyen hosszú a kezében levő bárd nyele. :-)
Ha mindketten pontszerűek, és Tom reakcióideje pozitív, akkor sík terepen sincs esélye elkapni Jerryt, akármennyivel is gyorsabb.
|
| Előzmény: [58] Pach Péter Pál, 2004-06-07 20:22:28 |
|
| [58] Pach Péter Pál | 2004-06-07 20:22:28 |
 Szerintem is csak 0-nak vehetjük, különben gondok lennének...
A baj az, hogy 0 reakcióidő esetén lehetséges, hogy egyszerre mindketten nem tudják megvalósítani stratégiájukat. Sőt, a legtöbb stratégia olyan, hogy a másik választhat olyan stratégiát, ami ellentmondást okoz. (A nyerő stratégiák is ilyenek.) A megoldás keresése közben mindig valakinek a szemszögéből figyeltük az eseményeket, és persze mindig tudtuk, hogy a másik abban a pillanatban éppen mit csinál, illetve mit fog csinálni. Ez szerintem akkor már teljesen korrekt, ha azt mondjuk, hogy a mi reakcióidőnk 0, a másiké tetszőlegesen kicsi pozitív (nem rögzített) érték. De a valódi játéknál egyiküket sem különböztethetjük meg hátrányosan.
|
| Előzmény: [57] Kós Géza, 2004-06-07 18:20:09 |
|
|
|
| [55] Kós Géza | 2004-04-16 13:18:37 |
 Jerry minden egyes helyzetéhez meghatározhatjuk azokat a pontokat a medence kerületén, ahonnan indulva Tom nyer. Ezek a pontok a kerület egy szakaszát alkotják. Ahogy Jerry közeledik a parthoz, a ,,nyerő szakasz'' egyre rövidül, végül egyetlen ponttá zsugorodik. Ha pedig Jerry távolodik a parttól, a nyerő szakasz egyre hosszabb lesz, és amikor Jerry eléri az EFGH négyzet kerületét, a szakasz két vége éppen összeér.
A nyerő szakasz két vége legfeljebb p-szer mozog gyorsabban, mint Jerry. Ezért Tom elérheti, hogy mindig a nyerő szakaszon legyen.
|
| Előzmény: [54] Pach Péter Pál, 2004-04-12 22:45:35 |
|
| [54] Pach Péter Pál | 2004-04-12 22:45:35 |
 Tényleg kulturáltabb az ilyen alak. Egy dolog még nem egészen világos a megoldásból. Tom stratégiája valahogy úgy szólhat, hogy a kedvezőbb irányban rohan, amíg nem kerül OJ félegyenesre (O a négyzet középpontja), ha már ezen van, akkor próbál rajta maradni. Ez utóbbit azonban nem mindig tudja megtenni: ha Jerry még „közel” van a medence közepéhez, akkor előfordulhat, hogy nagyobb a szögsebessége. Persze Jerry nem túl okos, ha EFGH utolsó elhagyása után „megengedi”, hogy OJT egy félegyenes legyen, amikor még a medence közepéhez közel van, mégsem látom elegáns kiküszöbölését ennek a problémának.
|
| Előzmény: [52] Kós Géza, 2004-04-09 12:03:08 |
|
| [53] Sirpi | 2004-04-12 15:19:49 |
 Csak eszembe jutott a feladat kapcsán, hogy ezt a p határsebességet lehet definiálni minden "szép" halmazra, pl. olyanokra, melyekben nincs luk, és a határuk véges hosszú folytonos görbe. Ezzel lehetne mondjuk mérni, hogy az adott halmaz mennyire "körszerű". Lehet, hogy kijönne ebből valami elmélet, bár egyelőre sok ötletem nincs a dologhoz...
S
|
| Előzmény: [52] Kós Géza, 2004-04-09 12:03:08 |
|
| [52] Kós Géza | 2004-04-09 12:03:08 |
 Szia Péter,
Bocs a lassú válaszért, az eredmény helyes. (Én jobban szeretem a  alakban írni, de ez lényegtelen.) alakban írni, de ez lényegtelen.)
Örülök, hogy sikerült a végére jutnunk. Kár, hogy a többiek csak csendes szemlélők voltak.
|
| Előzmény: [51] Pach Péter Pál, 2004-03-28 19:52:52 |
|
| [51] Pach Péter Pál | 2004-03-28 19:52:52 |
 Szia Géza,
Tömören írom le, de remélem nincs benne hiba.
[49]-hez hasonló linearitásból jön ki, hogy ha Jerry f(T)-ben hagyja el a belső négyzetet, ezek után Tom valamelyik irányban maximális sebességgel rohan, akkor mindig ugyanazt a kritikus p-t kapjuk – csak most E-t és F-et vizsgáljuk, nem pedig E-t és L-t. Jerry JX vagy JY irányban úszik Tom pillanatnyi sebességének  -szeresével. A még ki nem használt sebességével pedig JX és JY szögfelezőjének irányában halad. A „szögfelező-irányú” mozgással a megteendő utak arányát saját javára változtatja, különben pedig attól a pillanattól kell vizsgálni a „versenyt”, amikor Tom utoljára hagyja el T-t. (...) Tom akkor jár legjobban, ha valamelyik irányban teljes sebességével rohan. -szeresével. A még ki nem használt sebességével pedig JX és JY szögfelezőjének irányában halad. A „szögfelező-irányú” mozgással a megteendő utak arányát saját javára változtatja, különben pedig attól a pillanattól kell vizsgálni a „versenyt”, amikor Tom utoljára hagyja el T-t. (...) Tom akkor jár legjobban, ha valamelyik irányban teljes sebességével rohan.
A keresett p-t L-ből érdemes kiszámolni, a kapott egyenlet: 5sin2 +5sin +5sin  cos cos  –1=0. Ebből sin2 –1=0. Ebből sin2 -re másodfokú egyenletet kapunk, melynek megfelelő gyökét kiválasztva, és gyökének reciprokát véve a keresett p érték -re másodfokú egyenletet kapunk, melynek megfelelő gyökét kiválasztva, és gyökének reciprokát véve a keresett p érték  , ami körülbelül 5,7886. , ami körülbelül 5,7886.
|
| Előzmény: [50] Kós Géza, 2004-03-24 07:57:40 |
|
| [50] Kós Géza | 2004-03-24 07:57:40 |
 Szia Péter,
Most már csak az van hátra, hogy összefoglaljuk Tom és Jerry legjobb taktikáját, és kiszámoljuk a legkisebb sebességarányt, aminél Tom el tudja kapni Jerryt.
(Az utolsó mondatban tökéletesen igazad van.)
|
| Előzmény: [49] Pach Péter Pál, 2004-03-24 00:17:24 |
|
| [49] Pach Péter Pál | 2004-03-24 00:17:24 |
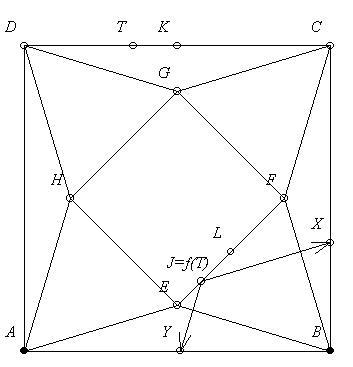
 CD és EF szakaszok felezőpontja legyen rendre K, L. Feltehetjük, hogy T(om) DK szakaszon található. Legyen mondjuk DT:TK= :(1- :(1- ). Azt állítjuk, hogyha Jerry EF szakasz azon J pontjában lép ki, amelyre LJ:JE= ). Azt állítjuk, hogyha Jerry EF szakasz azon J pontjában lép ki, amelyre LJ:JE= :(1- :(1- ), akkor mindegy, hogy Tom melyik irányt választja, egyikkel sem jár jobban, mint a másikkal. Mikor valósul ez meg? Megnézzük, hogy Jerrynek mennyivel kell többet úsznia, ha Tom a pozitív körüljárást választja, mintha a negatív mellett dönt. Legyen ez j. Ugyanígy, Tom pedig t-vel többet fut a pozitív irány esetén. Pontosan akkor mindegy, hogy Tom melyik irányt választja, ha t=pj. Tekintsük pl. a pozitív körüljárást. Ekkor Tom útja TD+DA+AB+BX, Jerryé pedig JX. Vegyük észre, hogy mind az öt szakasz-hossz ), akkor mindegy, hogy Tom melyik irányt választja, egyikkel sem jár jobban, mint a másikkal. Mikor valósul ez meg? Megnézzük, hogy Jerrynek mennyivel kell többet úsznia, ha Tom a pozitív körüljárást választja, mintha a negatív mellett dönt. Legyen ez j. Ugyanígy, Tom pedig t-vel többet fut a pozitív irány esetén. Pontosan akkor mindegy, hogy Tom melyik irányt választja, ha t=pj. Tekintsük pl. a pozitív körüljárást. Ekkor Tom útja TD+DA+AB+BX, Jerryé pedig JX. Vegyük észre, hogy mind az öt szakasz-hossz  -nak lineráris függvénye. Ez persze a másik körüljárás esetén is teljesül. Így a 0=pj-t egyenlet -nak lineráris függvénye. Ez persze a másik körüljárás esetén is teljesül. Így a 0=pj-t egyenlet  -ban elsőfokú. Ha -ban elsőfokú. Ha  =0, vagy =0, vagy  =1, akkor triviálisan teljesül az egyenlőség. (J=L-nél teljes a szimmetria, E pedig rajta van BE félegyenesen, így X-et kicserélhetjük arra a pontra, amelyik Y tükörképe AB felezőpontjára. A változtatás után megintcsak szimmetrikus a helyzet.) A függvényünk egy elsőfokú polinom, ezért a köztes =1, akkor triviálisan teljesül az egyenlőség. (J=L-nél teljes a szimmetria, E pedig rajta van BE félegyenesen, így X-et kicserélhetjük arra a pontra, amelyik Y tükörképe AB felezőpontjára. A változtatás után megintcsak szimmetrikus a helyzet.) A függvényünk egy elsőfokú polinom, ezért a köztes  -kra is teljesül az egyenlőség. -kra is teljesül az egyenlőség.
Már csak azt kell megnéznünk, hogy miért teljesül J=f(T) - ugyanis ezt állítjuk -, ha J-t a leírtak szerint határozzuk meg. Csak EF pontjait vizsgáljuk, a többi pont még egyszerűbben zárható ki. Tegyük fel, hogy f(T) J-től E felé esik. Tom a negatív körüljárást választja. Ha Jerry J-t választaná, akkor neki kevesebbet, Tomnak viszont többet kellene haladnia a „találkozási” pontig. Ha f(T) F felé esik, akkor Tom a negatív körüljárást választja, és megint azt kapjuk, hogy Jerry jobban járt volna J-vel. (Használtuk, hogy BEF háromszögön belül az ideális kiúszási irány már ismert.)
Tehát f(T)=J. Az f függvény pl. a DK-ra eső T-hez EL szakasz azon J pontját rendeli, amelyre DT:TK=LJ:JE.
A [42-44]-beli négyzeteknél kisebb EFGH, ez mondjuk a háromszög-egyenlőtlenségből következik. [44]-ben már rávilágítottál a lényegre: egy korábbi feladatban már igazoltuk, hogy ha Tom sebessége Jerry sebességének  -szörösénél kisebb, akkor Jerry el tudja érni, hogy a Tommal átellenes ponton lépjen ki a medencéből. Az ideális f(T) pont sebessége EFGH négyzet partján pedig Jerry sebességének -szörösénél kisebb, akkor Jerry el tudja érni, hogy a Tommal átellenes ponton lépjen ki a medencéből. Az ideális f(T) pont sebessége EFGH négyzet partján pedig Jerry sebességének  -szörösénél kisebb. Ez teljesül az f(T)-vel átellenes pontra is. Jerry azt képzeli, hogy ennek a pontnak a mozgátást követi egy Tom2 macska. -szörösénél kisebb. Ez teljesül az f(T)-vel átellenes pontra is. Jerry azt képzeli, hogy ennek a pontnak a mozgátást követi egy Tom2 macska.
EFGH négyzetre alkalmazzuk a korábbi feladat állítását, és éppen azt kapjuk, hogy Jerry el tudja érni EFGH partját a Tom2-vel átellenes pontban, azaz f(T)-ben.
(A kereszt szerintem nem felelne meg, mert előfordulhatna, hogy Jerrynek az ideális irányt követése közben keresztül kell haladnia rajta, azaz visszamenne T1-be. :-))
|
 |
| Előzmény: [48] Kós Géza, 2004-03-17 16:12:08 |
|
| [48] Kós Géza | 2004-03-17 16:12:08 |
 Én az EFGH négyzetre gondoltam. A bizonyítás mindig azon múlik, hogy az E, F, G, H pontokat kívülről kell megkerüni. (Így aztán az EG és FH szakaszok által alkotot kereszt is megfelelne. :-))
* * *
Tételezzük fel, hogy Tom a medence szélén, a T pontban áll mindaddig, amíg Jerry az EFGH négyzet belsejében van. Amikor viszont Jerry a négyzet határán vagy azon kívül van, Tom a ,,közelebbi'' irányban szalad. Jerry tehát kiválasztja az EFGH négyzeten a számára ,,legjobb'' pontot, amit f(T)-vel jelöl, oda úszik, majd -- a korábban meghatározott irányban -- egyenesen kiúszik a partra.
a) Határozzuk meg az f függvényt.
b) Igaz-e, hogy Jerry akkor is elérheti az f(T) pontot, ha Tom mozog?
|
 |
| Előzmény: [47] Pach Péter Pál, 2004-03-17 00:28:06 |
|
| [47] Pach Péter Pál | 2004-03-17 00:28:06 |
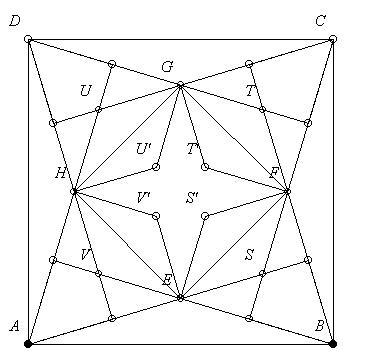
 Például ES'FT'GU'HV' nyolcszög is megfelel a feltételeknek. (Pl. S' úgy keletkezik, hogy S-t tükrözzük EF-re.)
ESFS' rombuszt a BFSE négyszöghöz csatlakoztatjuk. Az a korábbiakhoz hasonlóan látszik, hogy Jerrynek melyik partot kell választania; az ideális irány követése esetén nem úszhat vissza a középső tartmányba.
|
 |
| Előzmény: [46] Kós Géza, 2004-03-16 12:05:04 |
|
|
| [45] Pach Péter Pál | 2004-03-14 19:36:36 |
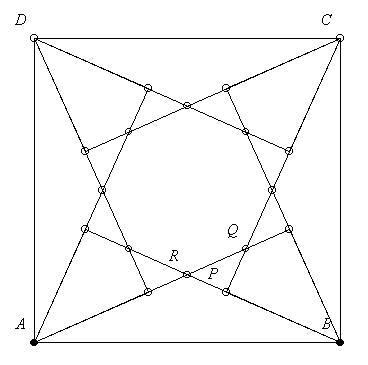
 A (színezetlen) kisháromszögeket még le lehet vágni T-ből. A megmaradó rész, egy nyolcszög lesz T1. Vegyük pl. PQR háromszöget! Ha Tom negatív körüljárás szerint jön, akkor világos, hogy Jerrynek AB-t érdemes választania. Az az érdekesebb eset, amikor Tom pozitív körüljárás szerint jön. Jerrynek ekkor BC-t kell választania. Ez nyilvánvalóan jobb, mint AB, hiszen PQR háromszög BR félegyenes BC felőli partjára esik (korábban már láttuk, hogy ez a vízválasztó). De Jerry CP félegyenesnek a CD felőli oldalán van, ezért ez elvileg jobban megérné neki, min BC. De feltettük, hogy T1-be már nem megy vissza, így, hogy CD-hez eljuthasson, feltétlenül érintenie kell CP félegyenest. Amikor éppen CP-n van, akkor BC és CD egyformán jó neki, ezért már az elején is BC-t kellett választania. DA ehhez hasonlóan zárható ki.
Tehát a sarkoknál lévő négyszögekhez még hozzá lehet csapni két-két kisháromszöget.
|
 |
| Előzmény: [44] Kós Géza, 2004-03-11 15:09:09 |
|
| [44] Kós Géza | 2004-03-11 15:09:09 |
 Szia Péter,
A  oldalú, négyzetnek a medence közepén van egy érdekes tulajdonsága. Feleltessük meg a medence határpontjait a négyzet pontjainak (például egy forgatva nyújtással). Ekkor Tom sebességének és a Jerrynek megfelelő pont sebességének az aránya éppen oldalú, négyzetnek a medence közepén van egy érdekes tulajdonsága. Feleltessük meg a medence határpontjait a négyzet pontjainak (például egy forgatva nyújtással). Ekkor Tom sebességének és a Jerrynek megfelelő pont sebességének az aránya éppen  , ami a [15-18] szerint egy nagyon nevezetes arány... , ami a [15-18] szerint egy nagyon nevezetes arány...
* * *
Egy kis segítség a folytatáshoz.
A 40-es hozzászólás ábráján, a medence közepén van egy csillag alakú, kiszínezetlen tartomány; jelöljük ezt T-vel. A T-n kívüli pontokban minenhol megadtunk két irányt, amerre Jerrynek úsznia érdemes attól függően, hogy Tom melyik irányból közeledik. Ha Jerry ki akar úszni a partra úgy, hogy közben már nem tér vissza T-be, akkor ezek a legjobb irányok.
A T tartományt ki lehet cserélni egy kisebb, egyszerűbb felépítésű T1-re, és a kiszínezett tartományokat meg lehet hosszabbítani úgy, hogy a fenti tulajdonságok érvényben maradjanak. Ez a következő részfeladat.
|
| Előzmény: [43] Pach Péter Pál, 2004-03-09 18:05:16 |
|
|
| [42] Kós Géza | 2003-12-18 11:39:23 |
 Én is ezen a ponton akadtam el egy időre. :-) Aki ismerte a klasszikus változat megoldását, annak az eddigiek lényegében rutin lépések voltak. Most kezdődik A megoldás...
Segítségként azt tanácsolom, hogy próbáld (próbáljátok) meg a sarkoknál levő tartományokat tovább folytatni és a középső csillagot kisebbíteni.
* * *
A keresendő alakzatról: A középen levő tartomány két négyzet egyesítése. Érdemes kiszámolni, mekkorák ezek a négyzetek, az eredmény nagyon érdekes.
Amikor a medence és a keresett görbe is kör volt, a kerületek arányát p-nek választottuk. A 15-18. hozzászólások viszont azt mutatják, hogy más alakzatok esetén más lehet a helyes arány.
|
| Előzmény: [41] Pach Péter Pál, 2003-12-17 21:13:51 |
|
| [41] Pach Péter Pál | 2003-12-17 21:13:51 |
 Géza, adj valami segítőlökést!
Azért írok, mert már majdnem két hete nem szólt hozzá senki sem a témához.
Most, leadási határidő után, szerintem felpezsdül a téma. Egyébként mi a cél? Először úgy gondoltam, hogy egy olyan 4/p kerületű (ha a négyzet egységnégyzet) zárt görbét keresünk (amely a négyzet „közepét” tartalmazza), és amelyre teljesül, hogy ha Jerry a Tommal átellenes pontján hagyja el (JT szakasz tartalmazza a négyzet középpontját), akkor a kritikus p mindig ugyanannyi. Ráadul ez a p megegyezik azzal a p-vel is, amivel előállítottuk az ábrát. De egy ilyen alakzat konkáv (?), ami problémát okoz(hat).
|
|
| [40] Kós Géza | 2003-12-04 11:30:41 |
 Jöjjön hát a négyzetes feladat megoldása. Hasonló stratégiákat szeretnénk, mint a klasszikus feladatban. A medence közepén lesz egy kis tartomány, ahol Jerry gyorsabb. Tom megvárja, amíg Jerry a tartomány határára ér, és akkor kezd el futni....
* * *
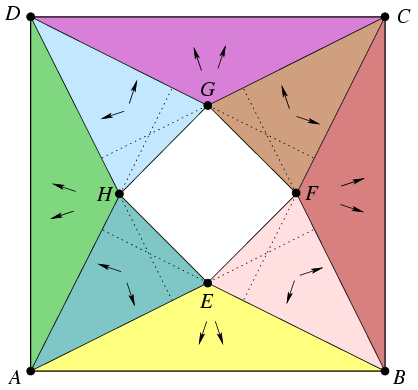
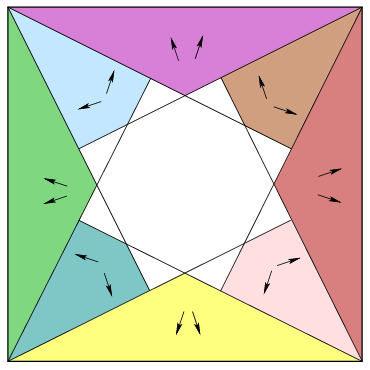
A négyzet minden csúcsában megrajzoljuk azt a két félegyenest, ami a szögfelezővel  szöget zár be, és kiszínezzük az ábrán látható nyolc tartományt. Ha Jerry valamelyik kiszínezett tartományban van, és úgy dönt, hogy ő most egyenesen kiúszik a partra, és nem érinti a középső, csillag alakú részt, akkor tudjuk, hogy milyen irányban érdemes úsznia. Mindig két lehetséges irány közül kell választania attól függően, hogy Tom melyik irányból érkezik. Ezeket az irányokat láthatjuk az ábrán. szöget zár be, és kiszínezzük az ábrán látható nyolc tartományt. Ha Jerry valamelyik kiszínezett tartományban van, és úgy dönt, hogy ő most egyenesen kiúszik a partra, és nem érinti a középső, csillag alakú részt, akkor tudjuk, hogy milyen irányban érdemes úsznia. Mindig két lehetséges irány közül kell választania attól függően, hogy Tom melyik irányból érkezik. Ezeket az irányokat láthatjuk az ábrán.
Most ti jöttök...
|
 |
|
| [39] Kós Géza | 2003-12-04 10:48:36 |
 Úgy látom, nehezebb feladatot kell adni. :-)
Az eredmény jó. (Az ilyen hosszú képleteket érdemes inkább több részre vágni.)
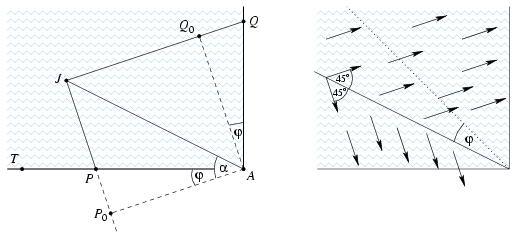
Nézzünk azért egy elemibb megoldást is. Legyen A merőleges vetülete a JP és JQ egyenesekre P0, illetve Q0 a baloldali ábra szerint.
Jerrynek akkor érdemes a Q pont felé úszni, ha  , azaz JQ-QQ0=JQ0 , azaz JQ-QQ0=JQ0 JP+PP0=JP0. A döntés tehát azon múlik, hogy az AP0JQ0 téglalapnak melyik oldala a hosszabb. Ha a JP0 a hosszabb, azaz JP+PP0=JP0. A döntés tehát azon múlik, hogy az AP0JQ0 téglalapnak melyik oldala a hosszabb. Ha a JP0 a hosszabb, azaz  >45o, akkor a Q pont felé érdemes úszni. Ha >45o, akkor a Q pont felé érdemes úszni. Ha  <45o, akkor pedig a P pont felé. Ha <45o, akkor pedig a P pont felé. Ha  =45o, akkor mindegy, hogy Jerry melyik pontot választja. =45o, akkor mindegy, hogy Jerry melyik pontot választja.
Az eredménynek több érdekes geometriai tartalma van. Érdemes meghúzni a szögfelezővel  szöget bezáró félegyenest. Jerrynek mindig az alapján kell döntenie, hogy a félegyenesnek melyik oldalán van. A legjobb irány pedig mindig 45 fokos szöget zár be a félegyenessel (jobboldali ábra). szöget bezáró félegyenest. Jerrynek mindig az alapján kell döntenie, hogy a félegyenesnek melyik oldalán van. A legjobb irány pedig mindig 45 fokos szöget zár be a félegyenessel (jobboldali ábra).
|
 |
| Előzmény: [38] Pach Péter Pál, 2003-12-04 01:14:59 |
|
| [38] Pach Péter Pál | 2003-12-04 01:14:59 |
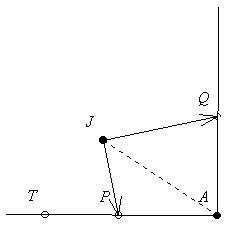
 A negyedsík csúcsa legyen A, Tom és Jerry kezdeti pozíciója pedig T, illetve J! Látszik, hogy Jerry döntését TAJ határozza meg. A kritkikus TAJ határozza meg. A kritkikus TAJ szög legyen szög legyen  ! Ha TAJ ! Ha TAJ < < , akkor Jerrynek nem érdemes levágnia a sarkot, ha viszont TAJ , akkor Jerrynek nem érdemes levágnia a sarkot, ha viszont TAJ > > , akkor az. (Ha TAJ , akkor az. (Ha TAJ = = , akkor mindegy, mit tesz Jerry.) , akkor mindegy, mit tesz Jerry.)
A továbbiakban  -t fogjuk meghatározni. A part két (Jerry által) kiszemelt pontja legyen P, illetve Q. Igazából az a kérdés, hogy Jerrynek több idő P helyett Q-ba úszni, vagy Tomnak P helyett Q-ig futni. A kritikus esetben a két időtartam egyenlő: -t fogjuk meghatározni. A part két (Jerry által) kiszemelt pontja legyen P, illetve Q. Igazából az a kérdés, hogy Jerrynek több idő P helyett Q-ba úszni, vagy Tomnak P helyett Q-ig futni. A kritikus esetben a két időtartam egyenlő:

Vegyük Jerry távolságát a part Tomot nem tartalmazó félegyenesétől egységnyinek! Ekkor: ( -t felhasználva) -t felhasználva)

1-tg  =sin =sin  cos cos  -tg -tg  sin2 sin2 +tg +tg  sin sin  cos cos  +sin2 +sin2



Tehát  =45o- =45o- . (Ha . (Ha  45o-nál nagyobb, akkor 45o-nál nagyobb, akkor  , és így Jerry könnyedén eléri a partot.) Tehát az érdekes esetekben az , és így Jerry könnyedén eléri a partot.) Tehát az érdekes esetekben az  határszög értéke 45o- határszög értéke 45o- . .
|
 |
| Előzmény: [37] Kós Géza, 2003-12-03 22:30:01 |
|
| [37] Kós Géza | 2003-12-03 22:30:01 |
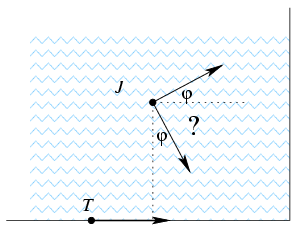
 Térjünk vissza a négyzet alakú tóhoz. Először azt vizsgáljuk meg, hogy mikor érdemes egy sarkot levágni.
Jerry most negyedsík alakú tóban úszik, Tom az egyik oldalon közeledik. Jerrynek el kell döntenie, hogy melyik partra ússzon. Ha ezt már eldöntötte, a pontos irányt már tudjuk, a legjobb irány a parttal 90o- szöget zár be, ahol szöget zár be, ahol  . .
Mikor ússzon Jerry az egyik, illetve a másik partra?
|
 |
|
| [36] Kós Géza | 2003-12-03 22:22:39 |
 Akkor hát összefoglalom a klasszikus feladat végeredményét.
Legyen  0 az a hegyesszög, amelyre 0 az a hegyesszög, amelyre  , és legyen , és legyen  . Ezek közelítő értéke . Ezek közelítő értéke  0 0 12,55o, illetve p0 12,55o, illetve p0 4,6033. 4,6033.
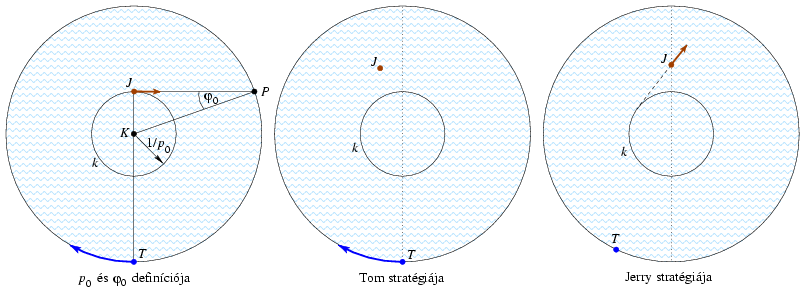
Ha a sebességek aránya p0, Jerry az 1/p0=sin  0 sugarú körön, a Tommal ellentétes pontról indul az érintő mentén, Tom pedig ugyanebben az irányban fut a kör mentén, akkor egyszerre érkeznek ugyanabba a P pontba (baloldali ábra). 0 sugarú körön, a Tommal ellentétes pontról indul az érintő mentén, Tom pedig ugyanebben az irányban fut a kör mentén, akkor egyszerre érkeznek ugyanabba a P pontba (baloldali ábra).
Tom stratégiája: Ha a sebességek aránya legalább p0, akkor Jerry akárhogyan is úszik ki a partra, Tom el tudja kapni. Amíg Jerry a k kör belsejében van, Tom tetszőlegesen viselkedhet, például egy helyben állhat. Amikor viszont Jerry k kerületén vagy azon kívül van, akkor Tom megvizsgálja, hogy Jerry a T-ből húzott átmérő melyik oldalán van, és abba az irányba fut (középső ábra).
Jerry stratégiája. Ha a sebességek aránya p0-nál kisebb, akkor Tom viselkedésétől függetlenül Jerry biztonságban ki tud úszni a partra. Jerry először a k kör kerületén úszik körbe addig, amíg a Tommal ellentétes pontra jut. Ezt elérheti, mert a szögsebessége nagyobb, mint Tomé. Ettől kezdve mindig a Tomot tartalmazú félsíkban, a k körhöz húzott érintő meghosszabbításán úszik (jobboldali ábra).
|
 |
| Előzmény: [35] Kós Géza, 2003-11-29 22:30:45 |
|
